Навигация
Таблица производных. Дифференцирование сложных функций
Контрольная работа
Дисциплина: Высшая математика
Тема: Таблица производных. Дифференцирование сложных функций
1. Таблица производных
Как известно, большинство функций можно представить в виде какой-то комбинации элементарных функций. Зная, как дифференцируются элементарные функции, можно продифференцировать и их различные комбинации. Поэтому рассмотрим таблицу производных элементарных функций.
1. ![]() .
.
Найдем производную, когда ![]() .
.
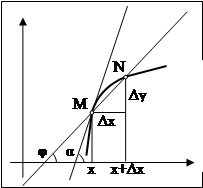
Зададим приращение аргументу ![]() , что даст
, что даст ![]() . Так как
. Так как
![]() , а
, а ![]() , то
, то

Отсюда 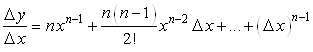 и
и 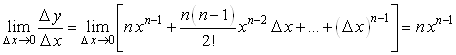 ,
,
то есть ![]() . Если
. Если ![]() , результат тот же.
, результат тот же.
2. ![]() .
.
Зададим приращение аргументу ![]() , что даст
, что даст ![]() . Так как
. Так как ![]() , а
, а ![]() , то
, то
![]() .
.
Отсюда  и
и 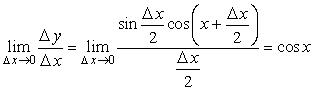 , то есть
, то есть ![]() .
.
3. ![]() .
.
Зададим приращение аргументу ![]() , что даст
, что даст ![]() . Так как
. Так как ![]() , а
, а ![]() , то
, то
![]() .
.
Отсюда 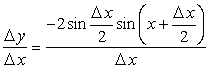 и
и 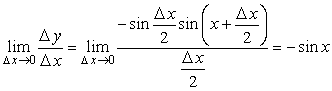 , то есть
, то есть ![]() .
.
4. ![]() .
.
По определению ![]() . Будем дифференцировать
. Будем дифференцировать ![]() как частное:
как частное:
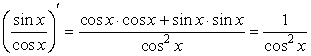 , то есть
, то есть ![]() .
.
5. ![]() .
.
По определению ![]() . Будем дифференцировать
. Будем дифференцировать ![]() как частное:
как частное:
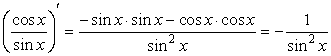 , то есть
, то есть ![]() .
.
6. ![]() .
.
Зададим приращение аргументу ![]() , что даст
, что даст ![]() . Так как
. Так как ![]() , а
, а ![]() , то
, то
![]() .
.
Отсюда 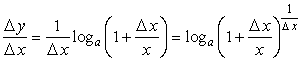 и
и
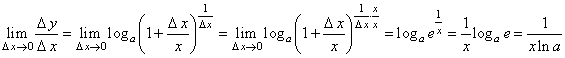 ,
,
то есть ![]() . Здесь была использована формула для второго замечательного предела.
. Здесь была использована формула для второго замечательного предела.
7. ![]() .
.
Для вычисления производной воспользуемся предыдущей формулой, в которой положим ![]() :
: ![]() . Значит,
. Значит, ![]() .
.
8. ![]() .
.
Зададим приращение аргументу ![]() , что даст
, что даст ![]() . Так как
. Так как ![]() , а
, а ![]() , то
, то ![]() . Отсюда
. Отсюда
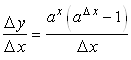 и
и  , то есть
, то есть ![]() .
.
Здесь была использована формула для одного из следствий из второго замечательного предела.
9. ![]() .
.
Для вычисления производной воспользуемся предыдущей формулой, в которой положим ![]() :
: ![]() . Значит,
. Значит, ![]() .
.
Прежде чем перейти к вычислению производных от обратных тригонометрических функций, рассмотрим вопрос о дифференцировании обратных функций вообще. Как было сказано в п. 8.2, для каждого взаимно однозначного отображения существует обратное отображение, то есть если ![]() , то
, то ![]() .
.
Теорема. Если для некоторой функции ![]() существует обратная ей
существует обратная ей ![]() , которая в точке
, которая в точке ![]() имеет производную не равную нулю, то в точке
имеет производную не равную нулю, то в точке ![]() функция
функция ![]() имеет производную
имеет производную ![]() равную
равную ![]() , то есть
, то есть 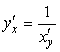 .
.
Доказательство. Рассмотрим отношение приращения функции к приращению аргумента: 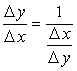 . Так как функция
. Так как функция ![]() имеет производную, то согласно теореме 11.2.2 она непрерывна, то есть
имеет производную, то согласно теореме 11.2.2 она непрерывна, то есть ![]() , откуда
, откуда 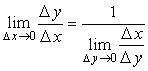 . Значит,
. Значит, 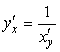 .
.
Воспользуемся данной теоремой для вычисления производных обратных тригонометрических функций.
10. ![]() .
.
В данном случае обратной функцией будет ![]() . Для нее
. Для нее ![]() . Отсюда
. Отсюда
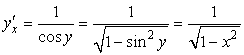 ,
,
то есть 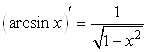 .
.
11. ![]() .
.
Так как
![]() , то
, то 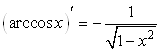 .
. ![]() .
.
В данном случае обратной функцией будет ![]() . Для нее
. Для нее
![]() .
.
Отсюда 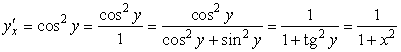 , то есть
, то есть ![]() .
.
13. ![]() .
.
Так как
![]() , то
, то ![]() .
.
Похожие работы
... Логарифмическое дифференцирование применяется для нахождения производной от показательно-степенной функции. Примеры 1. 2. . Таблица производных Объединим в одну таблицу все основные формулы и правили дифференцирования, выведенные ранее. Всюду будем полагать u=u(x), v=v(x), С=const. Для производных основных элементарных функций будем пользоваться теоремой о ...
... f ¢(xо) = 0, >0 (<0), то точка xоявляется точкой локального минимума (максимума) функции f(x). Если же =0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные. На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b]. Пример 3.22. Найти экстремумы функции f(x) ...
... функции в точке перегиба равна нулю, то есть = 0. Если вторая производная при переходе через некоторую точку меняет свой знак, то является точка перегиба ее графика. При исследовании функции и построении ее графика рекомендуется использовать следующую схему: Найти область определения функции. Исследовать функции на четность – нечетность (если функция четная или нечетная, то график ...
... дает: С помощью этой формулы можно получить несколько удобных формул для приближенных вычислений: Производная в школьном курсе алгебры 1. Структура учебников Колмогоров: §4. Производная 12. Приращение функции 13. Понятие о производной 14. Понятия о непрерывности и предельном переходе 15. Правила вычисления производных 16. Производная ...
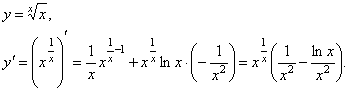


0 комментариев