Навигация
1. Окружность.
Возьмем точку ![]() на окружности с радиусом
на окружности с радиусом ![]() . Выражая
. Выражая ![]() и
и ![]() через гипотенузу прямоугольного треугольника, получаем:
через гипотенузу прямоугольного треугольника, получаем:
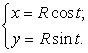
Это и есть уравнение окружности в параметрической форме (рис. 3.1). Возводя каждое уравнение в квадрат, отсюда легко получить обычное уравнение окружности ![]() .
.
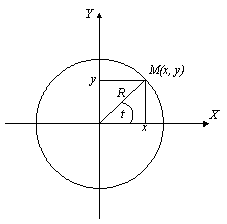
Рис. 3.1
2. Эллипс.
Известно, что уравнение эллипса – ![]() . Отсюда
. Отсюда ![]() . Возьмем две точки
. Возьмем две точки ![]() и
и ![]() на окружности и эллипсе, имеющие одинаковую абсциссу
на окружности и эллипсе, имеющие одинаковую абсциссу ![]() (рис. 3.2). Тогда из уравнения окружности следует, что
(рис. 3.2). Тогда из уравнения окружности следует, что ![]() . Подставим это выражение в
. Подставим это выражение в ![]() :
: ![]() . Значит, уравнение эллипса в параметрической форме имеет вид
. Значит, уравнение эллипса в параметрической форме имеет вид
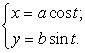
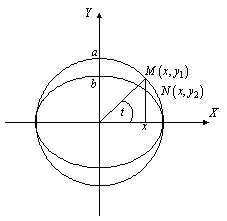
Рис. 3.2
3. Циклоида.
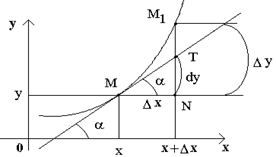
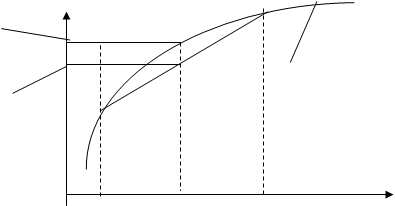
Пусть по ровной горизонтальной поверхности катится без скольжения окружность с радиусом ![]() . Зафиксируем точку O ее соприкосновения с поверхностью в начальный момент. Когда окружность повернется на угол t, точка O перейдет в точку C (рис. 3.3). Найдем ее координаты:
. Зафиксируем точку O ее соприкосновения с поверхностью в начальный момент. Когда окружность повернется на угол t, точка O перейдет в точку C (рис. 3.3). Найдем ее координаты:
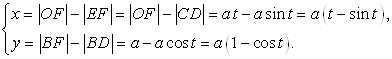
Значит, параметрическое уравнение циклоиды имеет вид:
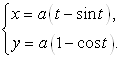
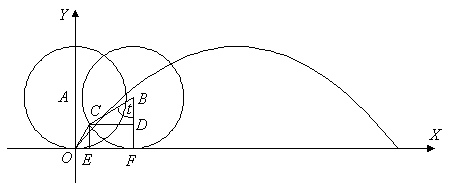
Рис. 3.3
4. Астроида.
Пусть внутри окружности радиуса ![]() без скольжения катится другая окружность радиуса
без скольжения катится другая окружность радиуса ![]() . Тогда точка меньшей окружности, которая в начальный момент времени была точкой соприкосновения с большей, в процессе движения опишет астроиду (рис. 3.4), параметрическое уравнение которой имеет вид:
. Тогда точка меньшей окружности, которая в начальный момент времени была точкой соприкосновения с большей, в процессе движения опишет астроиду (рис. 3.4), параметрическое уравнение которой имеет вид:
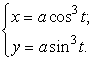
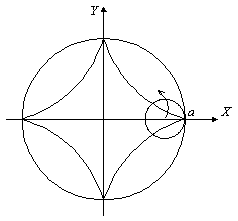
Рис. 3.4
Рассмотрев ряд примеров, перейдем теперь к вопросу о дифференцировании параметрически заданных функций.
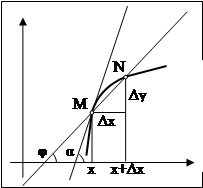
Пусть функция ![]() от
от ![]() задана параметрически:
задана параметрически: 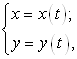 где
где ![]() . Пусть на этом отрезке обе функции имеют производные и при этом
. Пусть на этом отрезке обе функции имеют производные и при этом ![]() . Найдем
. Найдем ![]() .
.
Составим отношение ![]() . Тогда
. Тогда
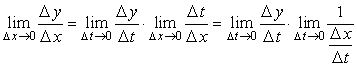 .
.
Следовательно, 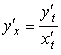 . Это и есть правило дифференцирования параметрически заданных функций.
. Это и есть правило дифференцирования параметрически заданных функций.
Литература
1. Бугров Я.С., Никольский С.М. ВЫСШАЯ МАТЕМАТИКА В 3-х томах Т. 1 Элементы линейной алгебры и аналитической геометрии 8-е изд. Изд-во: ДРОФА, 2006. – 284с.
2. Мироненко Е.С. Высшая математика. М: Высшая школа, 2002. – 109с.
3. Никольский С.М., Бугров Я.С. ВЫСШАЯ МАТЕМАТИКА В 3-Х ТОМАХ Т. 2 Дифференциальное и интегральное исчисление 8-е изд. Изд-во: ДРОФА, 2007. – 509с.
4. Черненко В.Д. Высшая математика в примерах и задачах. В трех томах. ПОЛИТЕХНИКА, 2003.
Похожие работы
... Логарифмическое дифференцирование применяется для нахождения производной от показательно-степенной функции. Примеры 1. 2. . Таблица производных Объединим в одну таблицу все основные формулы и правили дифференцирования, выведенные ранее. Всюду будем полагать u=u(x), v=v(x), С=const. Для производных основных элементарных функций будем пользоваться теоремой о ...
... f ¢(xо) = 0, >0 (<0), то точка xоявляется точкой локального минимума (максимума) функции f(x). Если же =0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные. На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b]. Пример 3.22. Найти экстремумы функции f(x) ...
... функции в точке перегиба равна нулю, то есть = 0. Если вторая производная при переходе через некоторую точку меняет свой знак, то является точка перегиба ее графика. При исследовании функции и построении ее графика рекомендуется использовать следующую схему: Найти область определения функции. Исследовать функции на четность – нечетность (если функция четная или нечетная, то график ...
... дает: С помощью этой формулы можно получить несколько удобных формул для приближенных вычислений: Производная в школьном курсе алгебры 1. Структура учебников Колмогоров: §4. Производная 12. Приращение функции 13. Понятие о производной 14. Понятия о непрерывности и предельном переходе 15. Правила вычисления производных 16. Производная ...


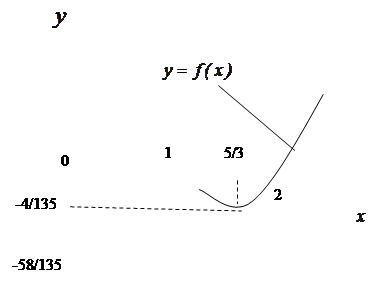
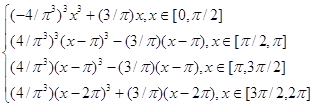
0 комментариев