Навигация
Производная сложной функции
7446
знаков
0
таблиц
6
изображений
2. Производная сложной функции
Пусть дана функция 
и при этом 
. Тогда исходную функцию можно представить в виде 
. Функции такого типа называются сложными. Например, 
.
В выражении аргумент 
называется промежуточным аргументом. Установим правило дифференцирования сложных функций, так как они охватывают практически все виды существующих функций.
Теорема. Пусть функция имеет производную в точке 
, а функция имеет производную в соответствующей точке . Тогда сложная функция в точке также будет иметь производную равную производной функции 
по промежуточному аргументу умноженной на производную промежуточного аргумента по , то есть 
.
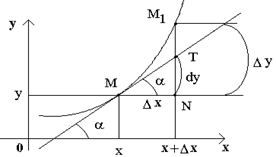
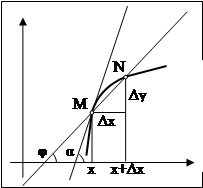
Для доказательства дадим приращение аргументу , то есть от перейдем к 
. Это вызовет приращение промежуточного аргумента , который от перейдет к 
. Но это, в свою очередь, приведет к изменению , который от перейдет к 
. Так как согласно условию теоремы функции 
и 
имеют производные, то в соответствии с теоремой о связи дифференцируемости и непрерывности функции (теорема 11.2.2) они непрерывны. Значит, если 
, то и 
, что, в свою очередь, вызовет стремление 
к нулю.
Составим 
. Отсюда,
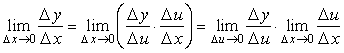
и, следовательно, .
Если функция 
имеет не один, а два промежуточных аргумента, то есть ее можно представить в виде , где 
, а 
, или 
, то, соответственно, 
и так далее.
3. Дифференцирование параметрически заданной функции
Выше были рассмотрены производные элементарных функций и указано правило дифференцирования сложных функций, составленных из элементарных. Но существуют и другие способы задания функций, которые также необходимо дифференцировать. Одним из таких способов является параметрическое задание функции, с которым мы уже сталкивались при изучении уравнения прямой линии.
При обычном задании функции уравнение связывало между собой две переменных: аргумент и функцию. Задавая , получаем значение , то есть пару чисел, являющихся координатами точки 
. При изменении меняется , точка начинает перемещаться и описывать некоторую линию. Однако при задании линии часто бывает удобно переменные и связывать не между собой, а выражать их через третью переменную величину.
Пусть даны две функции: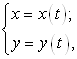 
где 
. Для каждого значения 
из данного промежутка будет своя пара чисел и , которой будет соответствовать точка . Пробегая все значения, заставляет меняться и , то есть точка движется и описывает некоторую кривую. Указанные уравнения называются параметрическим заданием функции, а переменная – параметром.
Если функция 
взаимно однозначная и имеет обратную себе, то можно найти 
. Подставляя в , получим 
, то есть обычную функцию. Указанная операция называется исключением параметра. Однако при параметрическом задании функции эту операцию не всегда делать удобно, а иногда и просто невозможно.
Так, в механике принят способ изображения траектории точки в виде изменения ее проекций по осям 
и 
в зависимости от времени , то есть в виде параметрически заданной функции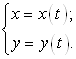 
Такой способ значительно удобнее при решении целого ряда задач. В трехмерном случае сюда добавляется еще и уравнение 
.
В качестве примера рассмотрим несколько параметрически заданных кривых.
Похожие работы
... Логарифмическое дифференцирование применяется для нахождения производной от показательно-степенной функции. Примеры 1. 2. . Таблица производных Объединим в одну таблицу все основные формулы и правили дифференцирования, выведенные ранее. Всюду будем полагать u=u(x), v=v(x), С=const. Для производных основных элементарных функций будем пользоваться теоремой о ...
... f ¢(xо) = 0, >0 (<0), то точка xоявляется точкой локального минимума (максимума) функции f(x). Если же =0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные. На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b]. Пример 3.22. Найти экстремумы функции f(x) ...
... функции в точке перегиба равна нулю, то есть = 0. Если вторая производная при переходе через некоторую точку меняет свой знак, то является точка перегиба ее графика. При исследовании функции и построении ее графика рекомендуется использовать следующую схему: Найти область определения функции. Исследовать функции на четность – нечетность (если функция четная или нечетная, то график ...
... дает: С помощью этой формулы можно получить несколько удобных формул для приближенных вычислений: Производная в школьном курсе алгебры 1. Структура учебников Колмогоров: §4. Производная 12. Приращение функции 13. Понятие о производной 14. Понятия о непрерывности и предельном переходе 15. Правила вычисления производных 16. Производная ...
0 комментариев