Навигация
Продольное обтекание тел вращения
1. Продольное обтекание тел вращения
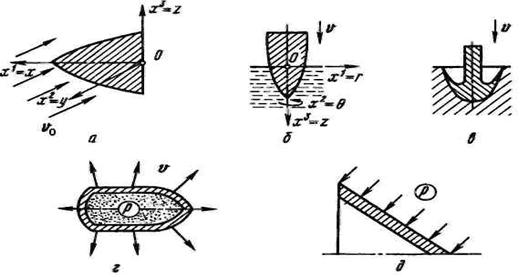
Для расчета внешнего осесимметричного обтекания тел вращения (см. Приложение 1) возьмем в меридианальных плоскостях (r, x) эллиптическую систему координат (x, h), связанную с (r, x) соотношениями
х = с ch x cos h, 0 £ x £ ¥,
r = с sh x sin h, 0 £ h £ 2p,
где величина c представляет расстояние фокусов семейства координатных линий – сoфокусных эллипсов и гипербол – от начала координат.
Положим
ch x = l, cos h = m, l £ l £ ¥, -1 £ m £ 1;
тогда связь между координатами (r, x) и (l, m) будет иметь вид
х = сlm, r = с Ö l2 – 1 Ö 1 – m2. (1)
Определив производные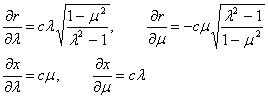
найдем коэффициенты Ламе[1]
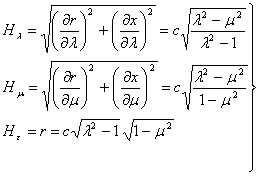 (2)
(2)
После этого уже нетрудно составить и основное дифференциальное уравнение Лапласа для потенциала скоростей. Согласно формуле[2]
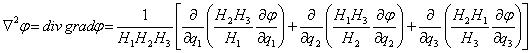 (*)
(*)
получим ![]() (3)
(3)
Будем искать частное решение этого уравнения в виде произведения двух функций от переменных l и m в отдельности
j = L(l) M(m); (4)
тогда в уравнении (2) переменные разделятся и из равенства
![]()
в силу независимости l и m будет следовать, что каждая из частей равенства должна быть постоянной. Полагая эту постоянную равной n (n+1), где n – целое положительное число, получим для определения L(l) и М(m) два обыкновенных линейных уравнения второго порядка лежандрова типа
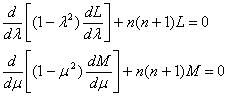 (5)
(5)
Этим уравнениям удовлетворяют[3] два класса независимых решений:
1) функции Лежандра 1-го рода – полиномы Лежандра Pn (х), определяемые равенствами
2)
P0(x) = 1, Р1(х) = х, P2(x) = 0.5 (Зх2-1), P3(x) = 0.5 (5x3-3x),…
и рекуррентным соотношением для вычисления последующих полиномов
(n + 1) Pn +1(х) = (2n + 1) хРn(х) – nРn-1(х);
2) функции Лежандра 2-го рода Qn(х), определяемые равенствами
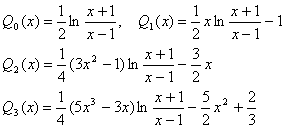
и рекуррентным соотношением
(n + 1) Qn+1(х) = (2n + 1) xQn(х) – nQn-1(х),
совпадающим с предыдущим соотношением для полиномов Лежандра.
Представим решение уравнения (3) как сумму двух потенциалов: 1) потенциала j¥ однородного потока, набегающего на тело со скоростью U¥; этот потенциал по первой из формул (1) будет равен j¥ = U¥x = U¥clm. и 2) потенциала j' скоростей возмущений, который выразим суммой частных решений (4).
Функция Pn(х), как полином n-й степени, обращается в бесконечность при бесконечно возрастающем аргументе, функция же Qn(х) при этом стремится к нулю, но зато логарифмически бесконечна при х = ± 1. В случае внешнего обтекания тела координата l = ch x может достигать бесконечных значений, а координата m ограничена. Примем во внимание, что потенциал скоростей возмущенного движения (т.е. обтекания за вычетом однородного потока со скоростью, равной скорости на бесконечности) должен стремиться к нулю при удалении от поверхности тела, причем ![]() .
.
Из приведенных соображений следует, что искомые частные решения должны иметь вид произведений Qn(l) Pn(m) (n = 1, 2,…);
подчеркнем, отсчет n при суммировании начинается с единицы, а не с нуля. Это подтверждается наличием следующих очевидных асимптотических равенств, справедливых при больших значениях l, а, следовательно, согласно (1), и R = = Ö х2 + r2, имеющего тот же порядок, что и l:
![]()
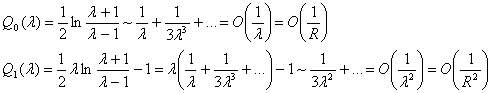
Таким образом, будем иметь правильный порядок убывания j' на бесконечности, если положим
![]() , (6)
, (6)
где An- постоянные коэффициенты, зависящие от формы поверхности тела.
Складывая потенциалы j¥ и j', получим искомый потенциал скоростей продольного обтекания тела вращения со скоростью на бесконечности, равной U¥,
![]() (7)
(7)
Для определения коэффициентов An найдем выражение функции тока y. По формуле (2) будем иметь
![]()
или после подстановки разложения (7)

Переписывая второе равенство в виде
![]()
подставим под знак суммы выражение для Pn из основного дифференциального уравнения функций Лежандра (5)
![]()
Тогда будем иметь
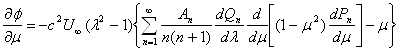
Интегрируя по m и добавляя необходимую функцию от l, получим окончательное выражение для функции тока
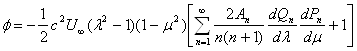 (8)
(8)
Уравнение нулевой поверхности тока будет
![]() (9)
(9)
Сравнивая его с заданным уравнением профиля тела вращения в эллиптических координатах, можно определить величины коэффициентов Аn, что и решает задачу. Конечно, именно этот пункт и является наиболее сложным с вычислительной стороны.
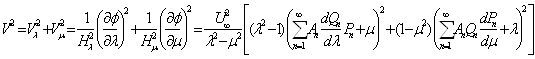
Имея выражение потенциала скоростей, найдем скорость по формуле (10).
Похожие работы
... и трещинами. Решение построено на использовании теории функции комплексного переменного и удовлетворении граничным условиям методом наименьших квадратов. 1 Термодинамические основы термоупругости 1.1 Термоупругость Основное уравнение термоупругости. При термическом расширении изотропное тело деформируется таким образом, что компоненты деформации отнесенные к системе прямоугольных осей ...
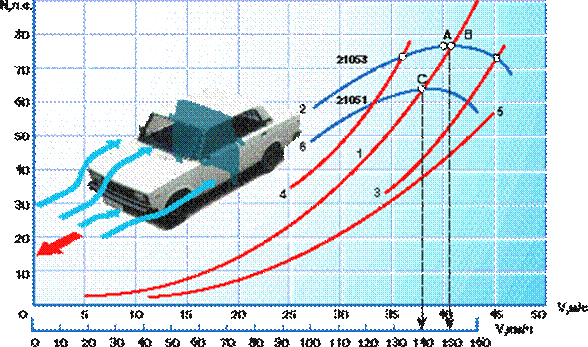
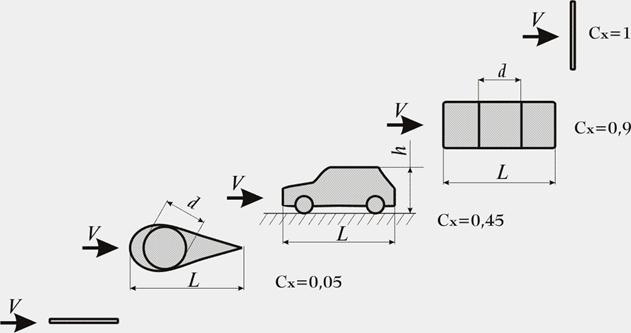
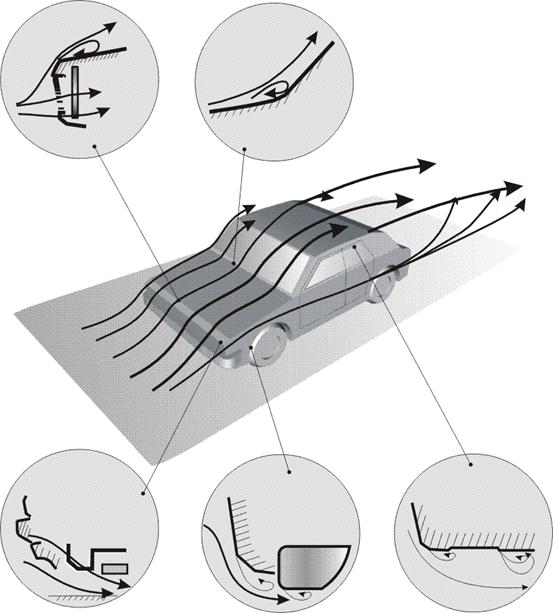
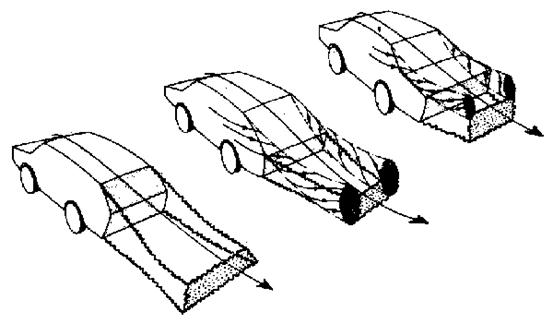
... увеличении скорости движения транспортного средства в два раза, сила сопротивления воздуха увеличивается в четыре раза, а затраты мощности вырастают в восемь раз!!! Поэтому при движении автомобиля в городском потоке аэродинамическое сопротивление автомобиля мало, на трассе же его значение достигает больших величин. А что говорить о гоночных болидах, движущихся со скоростями 300 км/час. В таких ...
... ребрами) изображают конструктивные и потоковые функциональные структуры [14]. Принципы построения функциональных структур технических объектов рассматриваются в последующих главах курса "Основы проектирования им конструирования" не включенных в настоящее пособие. Для систем управления существуют характеристики, которые можно использовать в качестве критериев для оценки структур. Одна из них - ...
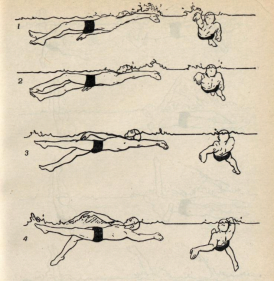
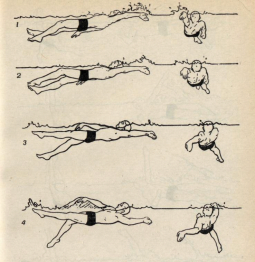
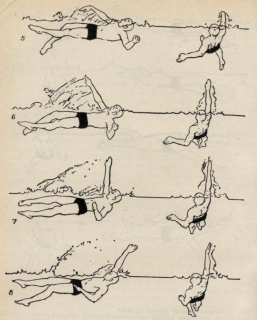
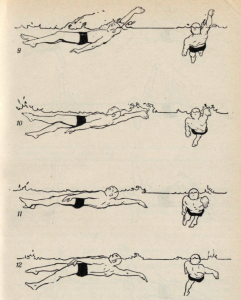
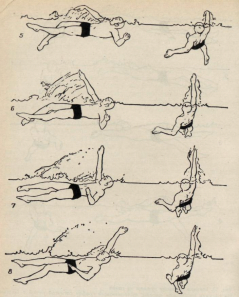
... - выдох (через нос или через рот и нос одновременно). Следует осуществлять полный выдох, который является необходимым условием для последующего полного вдоха. [1] 3. Биокинематическая схема плавания способом "кроль на спине" На рисунке 1 изображен пловец, выполняющий гребок согнутой рукой с шестью ударами ног на каждый цикл движений рук. Для определения глубины гребка рукой смотри вид сбоку. ...









0 комментариев