Навигация
Продольное и поперечное обтекание удлиненных тел вращения
3. Продольное и поперечное обтекание удлиненных тел вращения
В большинстве практических приложений приходится иметь дело с телами вращения, удлинение которых, т.е. отношение длины к максимальной толщине, довольно велико (порядка 8–12). Это объясняется хорошей обтекаемостью такого рода тел реальной жидкостью.
Расчет обтекания тел вращения большого удлинения может быть произведен приближенным методом. Изложим его основную идею[5].
Основным затруднением в решении задачи является определение коэффициентов Аn при продольном и Сn – при поперечном обтекании тела. Чем проще будет связь между l и m, определяющая форму контура в меридианной плоскости, тем меньше коэффициентов Аn, Сn можно брать в разложениях потенциала скоростей. Самая простая связь представляется равенством l = const, т.е. случаем обтекания эллипсоида. Отсюда следует вывод: чем ближе исследуемое тело по форме к эллипсоиду, тем легче может быть разрешена задача. В связи с этим решим, прежде всего, вопрос о выборе положения начала координат на продольной оси тела. Замечу, что фокусы удлиненного эллипсоида вращения находятся посередине отрезка, соединяющего точки пересечения большой оси и поверхности эллипсоида с центром кривизны поверхности в этих точках. Начало координат следует выбирать совпадающим с серединой отрезка, соединяющего фокусы; при таком выборе начала координат, чем ближе обтекаемое тело к эллипсоиду, тем меньше уравнение контура будет отличаться от простейшего равенства l = const.
Если обтекаемое тело имеет большое удлинение, то поверхность его располагается в области значений l, мало превышающих значение l = сhx = 1 или x = 0, соответствующее отрезку оси Oz, соединяющему фокусы. Рассматривая значения функций Qn(l) и dQn/dl при l, лишь немного превышающих единицу, убедимся, что при достаточно малых x будут иметь
место равенства
![]() (18)
(18)
где gn и dn – малые по сравнению с первыми членами поправки. Замечательно, что согласно равенствам (18), при малых x все функции Qn и dQn/dl в первом приближении не зависят от индекса n. Основное граничное условие продольного обтекания (9) в первом приближении будет, согласно (18), иметь вид
![]() (19)
(19)
где производная dPn/dm представляет известную функцию величины m = cos h. Ограничивая сумму некоторым фиксированным числом членов n = m, можно, пользуясь выражениями полиномов Лежандра (из § 1), написать тождество
![]() (20)
(20)
из которого можно вывести выражения коэффициентов An через an. Так, например, при m = 5 имеем
A1 = a1 – 3/5 a3 + 3/35 a5, A2 = a2 – 9/7 a4, A3 = 8/5 a3 – 32/15 a5,
A4 = 16/7 a4, A5 = 64/21 a5.
Представив контур меридианного сечения приближенным тригонометрическим разложением в эллиптических координатах
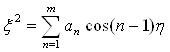 (21)
(21)
определим тем самым числа аn, а уже после этого, согласно тождеству (20), и величины коэффициентов An, что и дает первое приближение к решению задачи об осесимметричном продольном обтекании удлиненного тела вращения. Если удлинение обтекаемого тела велико, то указанное приближение оказывается для практики достаточным. При желании можно учесть в формулах (18) остаточные члены gn и dn, что приведет ко второму и следующим приближениям.
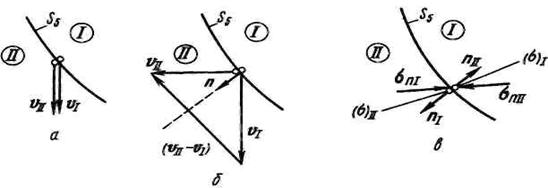
Аналогичным путем решается вопрос о поперечном обтекании удлиненного тела вращения. При плавности контура l изменяется в пределах от 1 + ½ x2min до 1 + ½ x2max; при этом m остается в пределах ±1. Таким образом, можно считать, что производная dl/dm имеет порядок x2max, т.е. сравнительно мала. Отсюда следует, что величина
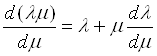
имеет порядок единицы. Рассматривая граничное условие (17) видим, что стоящая в квадратной скобке слева величина
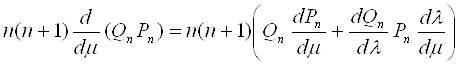
мала по сравнению с величиной ![]() . Действительно,
. Действительно,
![]()
Таким образом, в квадратной скобке в левой части равенства (*) первый одночлен имеет при малых x порядок 1/x2, второй – ln 1/x.
Из приведенного рассуждения следует, что на поверхности удлиненного тела вращения, где x мало, точное граничное условие поперечного обтекания (17) может быть заменено на приближенное
![]() (22)
(22)
Сравнивая это граничное условие с приближенным граничным условием продольного обтекания (19), видим, что между искомыми коэффициентами An и Cn существует простое соотношение
Cn = -2An/n (n+1). (23)
В первом приближении обе задачи – продольного и поперечного обтекания – решаются одновременно и сравнительно легким путем. При обычных значительных удлинениях тел вращения вполне можно довольствоваться первым приближением.
Определив коэффициенты An и Cn, найду выражения потенциалов и компонент скоростей для продольного и поперечного обтеканий, после чего уже нетрудно разыскать и распределение скоростей и давлений по поверхности заданного тела вращения или вне его при любом угле. Отмечу, что при всех вычислениях на поверхности удлиненного тела и вблизи нее можно пользоваться для Qn и dQn/dl приближенными выражениями (18). Само собой разумеется, что при удалении от поверхности обтекаемого тела l возрастает и формулы (18) становятся все менее и менее точными.
Похожие работы
... и трещинами. Решение построено на использовании теории функции комплексного переменного и удовлетворении граничным условиям методом наименьших квадратов. 1 Термодинамические основы термоупругости 1.1 Термоупругость Основное уравнение термоупругости. При термическом расширении изотропное тело деформируется таким образом, что компоненты деформации отнесенные к системе прямоугольных осей ...
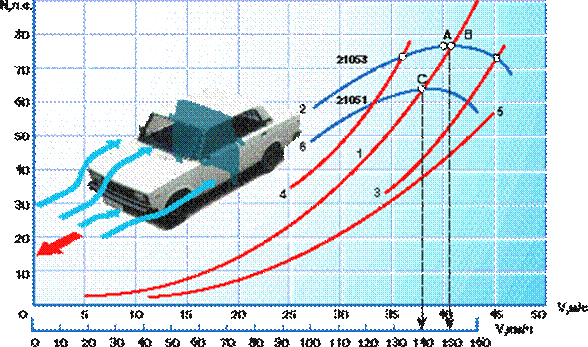
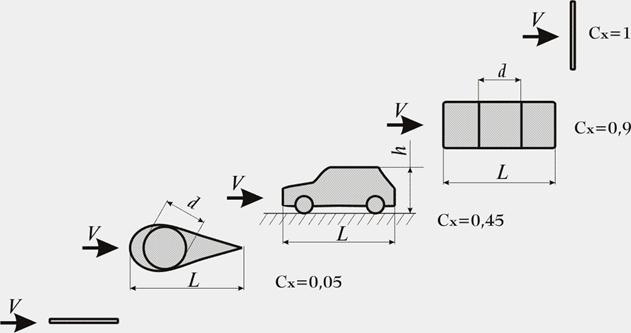
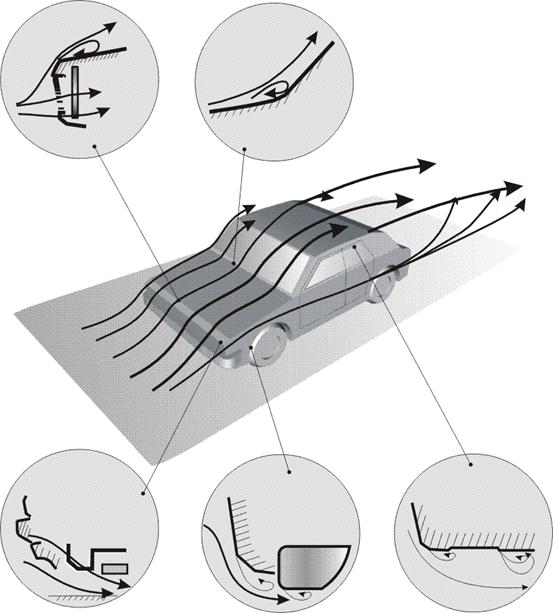
... увеличении скорости движения транспортного средства в два раза, сила сопротивления воздуха увеличивается в четыре раза, а затраты мощности вырастают в восемь раз!!! Поэтому при движении автомобиля в городском потоке аэродинамическое сопротивление автомобиля мало, на трассе же его значение достигает больших величин. А что говорить о гоночных болидах, движущихся со скоростями 300 км/час. В таких ...
... ребрами) изображают конструктивные и потоковые функциональные структуры [14]. Принципы построения функциональных структур технических объектов рассматриваются в последующих главах курса "Основы проектирования им конструирования" не включенных в настоящее пособие. Для систем управления существуют характеристики, которые можно использовать в качестве критериев для оценки структур. Одна из них - ...
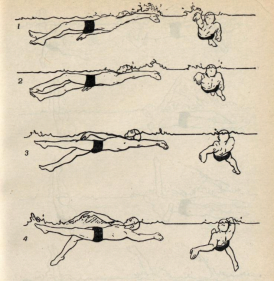
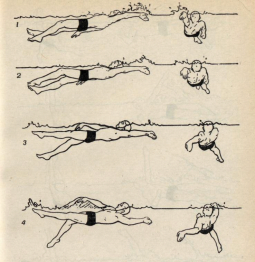
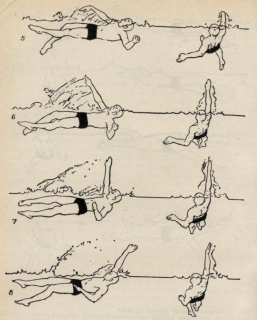
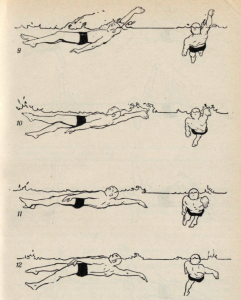
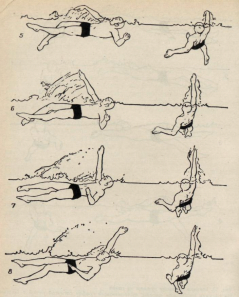
... - выдох (через нос или через рот и нос одновременно). Следует осуществлять полный выдох, который является необходимым условием для последующего полного вдоха. [1] 3. Биокинематическая схема плавания способом "кроль на спине" На рисунке 1 изображен пловец, выполняющий гребок согнутой рукой с шестью ударами ног на каждый цикл движений рук. Для определения глубины гребка рукой смотри вид сбоку. ...









0 комментариев