Навигация
Применение метода особенностей для расчета продольного и поперечного обтеканий тел вращения
4. Применение метода особенностей для расчета продольного и поперечного обтеканий тел вращения
Изложенный в предыдущих параграфах (§ 1 и § 2) метод исследования продольного и поперечного обтеканий тел вращения, основанный на непосредственном решении уравнения Лапласа в эллиптических координатах, не является единственным методом решения этой задачи. Первоначально формы обтекаемых тел вращения для дирижаблей определялись наложением однородного, параллельного некоторой оси потока на поток от системы источников (стоков), распределенных вдоль той же оси. Для этой цели применялись вначале дискретные особенности потока – системы источников (стоков) или диполей, а впоследствии – непрерывные их распределения.
Предположим для определенности, что на отрезке (– с, + с) оси Ох задано непрерывное распределение источников (стоков) интенсивности q(х). Тогда потенциал j' возмущенного движения, созданного этой системой особенностей, будет равен (знак минус введем в определение интенсивности q)
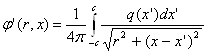 (24)
(24)
Если задаться видом функции q(x'), то, вычисляя интеграл (24), получим потенциал скоростей, а дифференцирование по r и x позволит вычислить и проекции скорости Vr и Vx. Наоборот, задаваясь формой обтекаемого тела, можно, переходя от потенциала скоростей возмущенного движения к полному потенциалу продольного обтекания тела однородным потоком с заданной скоростью на бесконечности и написав условие непроницаемости поверхности тела, получить интегральное уравнение, в котором q(х') будет неизвестной функцией. Заменяя потенциал скоростей на функцию тока, Карман[6] разработал метод приближенного интегрирования соответствующего интегрального уравнения, основанный на замене интеграла конечной суммой. Однако метод Кармана не был достаточно общим и, кроме того, требовал решения в каждом отдельном случае системы большого числа линейных алгебраических уравнений, что делало его на практике слишком трудоемким.
Аналогично, пользуясь выражением потенциала диполя: – m cosq / (4pr2), можно составить и потенциал j¢ поперечного обтекания тела вращения, складывая потенциал однородного натекания с заданной скоростью на бесконечности с потенциалом скоростей возмущенного движения жидкости от непрерывно распределенных по отрезку – с < х < с диполей интенсивности m(х')
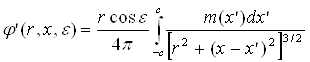 (25)
(25)
Здесь также можно задаваться распределением интенсивности m (х') или, наоборот, определять эту интенсивность из интегрального уравнения, представляющего условие непроницаемости заданной поверхности тела по отношению к потоку, складывающемуся из возмущенного и однородного на бесконечности.
Не останавливаясь на изложении этих в настоящее время уже малоупотребительных методов, укажем лишь на простую их связь с методами, изложенными в предыдущих параграфах. Покажем, что при заданной форме поверхностей обтекаемых тел вращения неизвестные функции q(х') и m(х') могут быть выражены через ранее введенные коэффициенты An и Сn.
Разобьем ось симметрии тела вращения Ох на две области: одну, определяемую интервалом – с £х£ с, заполненным особенностями, и вторую, представляющую остальную часть оси Ох, где | x | > c. В эллиптических координатах l, m отрезок, на котором расположены особенности, можно представить, согласно формуле r = c Ö l2 – 1 Ö 1 – m2, так:
l = 1, – 1 £ m £ 1,
а остальную часть оси Ох, как
m = ±1, 1 < l < ¥.
Тогда, сравнивая между собой вне отрезка (– с < х' < с) выражения потенциалов возмущений (24) и (25) с соответственными выражениями тех же потенциалов и приняв во внимание, что Рn(1) = 1, получим следующие два равенства:
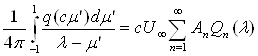 (26)
(26)
![]() (27)
(27)
которые при заданных коэффициентах An и Сn можно рассматривать как два интегральных уравнения для определения неизвестных функций q и m.
Интегральное уравнение (26) может быть решено, если искать решение в виде ряда ![]() , – 1 £ m' £ 1. Подставляя это разложение в (26), получим
, – 1 £ m' £ 1. Подставляя это разложение в (26), получим
![]()
Замечая, что по известной формуле теории функций Лежандра[7]
![]()
перепишем предыдущее интегральное уравнение в виде
![]()
откуда будет сразу следовать искомое решение
an = 2pcU¥An, ![]() (28)
(28)
Для разыскания второй неизвестной функции m(х') продифференцируем раз по l и другой раз по m' известное разложение[8]
![]()
![]()
тогда получим
![]()
Подставляя это разложение в интегральное уравнение (27), преобразуем его к виду
![]()
Используя далее разложение неизвестной функции m (cm¢) в форме
![]()
и замечая, что в силу ортогональности полиномов Лежандра
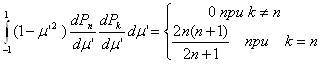
убедимся в справедливости равенства cn = Сn.
Итак, имеем
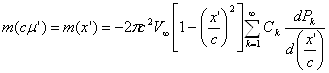 (29)
(29)
Совокупности формул (24) и (28), (25) и (29) позволяют при желании пользоваться потенциалами скоростей возмущений в цилиндрических координатах, если уже заранее вычислены коэффициенты An и Сn. Замечу, что эти коэффициенты проще определять при помощи разложений уравнения контура меридианного сечения в ряды по функциям от эллиптических координат, а уже затем проводить расчеты в эллиптических или цилиндрических координатах. Как было показано в предыдущем параграфе, в случае удлиненных тел коэффициенты An и Сn легко определяются путем разложения уравнения контура в тригонометрический ряд по косинусам эллиптической координаты h.
Замечу еще в заключение, что для тел с очень большим удлинением можно определить q(х) и m(х) из следующих двух простейших предположений:
1) в случае продольного обтекания считать нормальную к поверхности тела составляющую скорости возмущения V¢n равной скорости плоского движения от источника, расположенного в ближайшей точке оси. Тогда условие непроницаемости поверхности даст
V¢n = q(x) / 2pr = U¥ dr/dx,
откуда
q(x) = 2pU¥r dr/dx = U¥ dA/dx, (30)
причем r(x) представляет заданное уравнение контура меридианного сечения, A – площадь поперечного сечения;
2) в случае поперечного обтекания тела вращения выберем m(x) из условия, чтобы элемент тела, вырезанный плоскостями х и х + dx, обтекался так же, как элемент цилиндра бесконечного размаха в плоском движении. Это приведет к равенству
m(х) = 2pV¥r2(х) = 2V¥A(х). (31)
Список использованных источников
1. Лойцянский Л.Г., Механика жидкости и газа, Главная редакция физико-математической литературы издательства «Наука», М., 1987 г.
2. Е. Уиттекер и Г. Ватсон, Курс современного анализа
3. Я.М. Серебрийский, Обтекание тел вращения, т. VIII
4. Н.Я. Фабрикант, Курс аэродинамики, ч. I
5. И.А. Кибель, Н.Е. Кочин и Н.В. Розе, Теоретическая гидромеханика, ч. I
6. Г. Ламб, Гидродинамика.
[1] Е. Уиттекер и Г. Ватсон, Курс современного анализа, ч. II, стр. 85
[2] Лойцянский Л.Г., Механика жидкости и газа, Главная редакция физико-математической литературы издательства «Наука», М., 1987 г.
[3] Е. Уиттекер и Г. Ватсон, Курс современного анализа, ч. II, с. 91
[4] Е. Уиттекер и Г. Ватсон, Курс современного анализа, ч. II, стр. 119.
[5] Я.М. Серебрийский, Обтекание тел вращения, т. VIII.
[6] Н.Я. Фабрикант, Курс аэродинамики, ч. I, гл. III.
[7] Уиттекер и Ватсон, Курс современного анализа, ч. II, с. 114
[8] Уиттекер и Ватсон, Курс современного анализа, ч. II, стр. 117.
Похожие работы
... и трещинами. Решение построено на использовании теории функции комплексного переменного и удовлетворении граничным условиям методом наименьших квадратов. 1 Термодинамические основы термоупругости 1.1 Термоупругость Основное уравнение термоупругости. При термическом расширении изотропное тело деформируется таким образом, что компоненты деформации отнесенные к системе прямоугольных осей ...
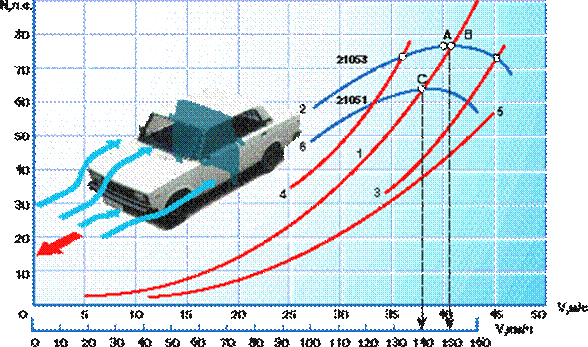
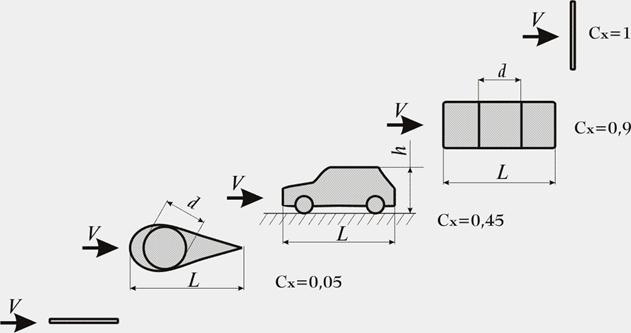
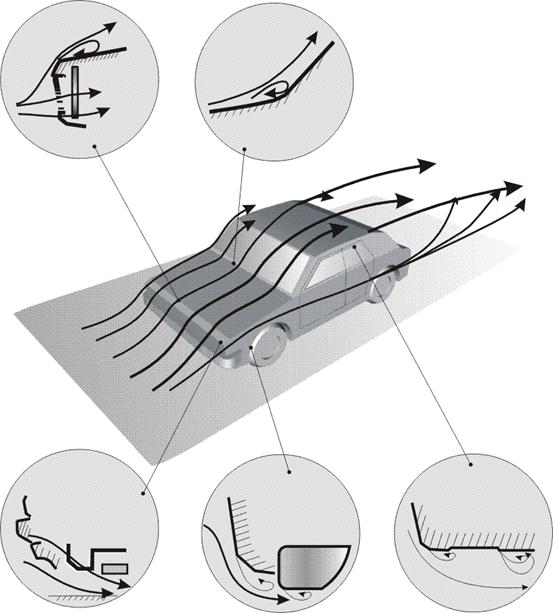
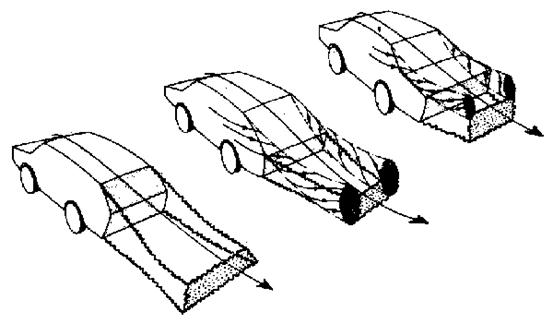
... увеличении скорости движения транспортного средства в два раза, сила сопротивления воздуха увеличивается в четыре раза, а затраты мощности вырастают в восемь раз!!! Поэтому при движении автомобиля в городском потоке аэродинамическое сопротивление автомобиля мало, на трассе же его значение достигает больших величин. А что говорить о гоночных болидах, движущихся со скоростями 300 км/час. В таких ...
... ребрами) изображают конструктивные и потоковые функциональные структуры [14]. Принципы построения функциональных структур технических объектов рассматриваются в последующих главах курса "Основы проектирования им конструирования" не включенных в настоящее пособие. Для систем управления существуют характеристики, которые можно использовать в качестве критериев для оценки структур. Одна из них - ...
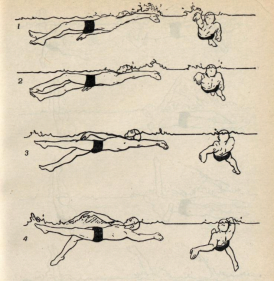
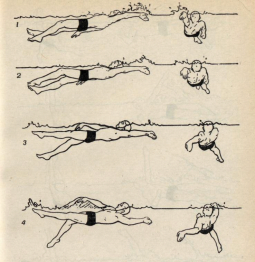
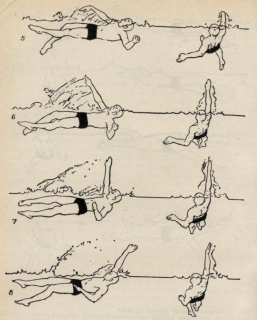
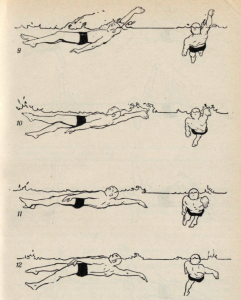
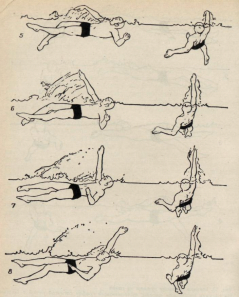
... - выдох (через нос или через рот и нос одновременно). Следует осуществлять полный выдох, который является необходимым условием для последующего полного вдоха. [1] 3. Биокинематическая схема плавания способом "кроль на спине" На рисунке 1 изображен пловец, выполняющий гребок согнутой рукой с шестью ударами ног на каждый цикл движений рук. Для определения глубины гребка рукой смотри вид сбоку. ...









0 комментариев