Навигация
Поперечное обтекание тел вращения
2. Поперечное обтекание тел вращения
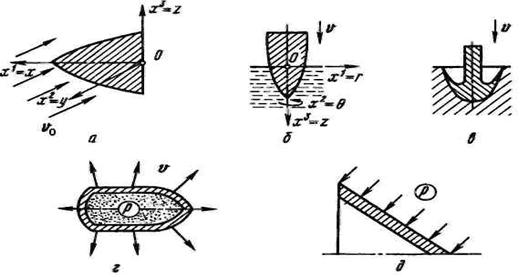
Наряду с продольным обтеканием тел вращения представляет интерес и поперечное обтекание, перпендикулярное (Приложение 1, б) к оси симметрии тела. Из сложения этих двух потоков можно получить обтекание тела вращения под любым углом.
В этом случае уже не получается осесимметричного движения. Уравнение Лапласа, определяющее потенциал скоростей, будет в ортогональной системе криволинейных координат, согласно (*), иметь вид
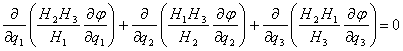
Сохраняя ту же систему координат (l, m, e), что и в случае осесимметричного обтекания тела вращения, и используя выражения коэффициентов Ламе (2), перепишем предыдущее уравнение в форме
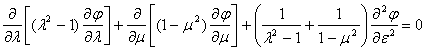 (13)
(13)
j = N(l, m) Е(e);
тогда, подставляя последнее выражение в уравнение (13) и разделяя функции независимых переменных, получим систему уравнений (k – произвольное число, которое будем считать положительным и целым)
![]()
Первое уравнение имеет решение: Е = A cos ke + В sin ke;
второе, если положить N = L(l) М(m) и разделить переменные, может быть приведено к системе уравнений
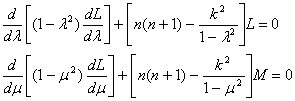
имеющей в качестве частных решений так называемые присоединенные функции Лежандра[4]
![]() (14)
(14)
Комбинируя эти функции так, чтобы выражение потенциала скоростей возмущенного движения было ограниченным при l ® ¥, получим общее выражение потенциала скоростей
![]()
здесь последнее слагаемое представляет собой потенциал скоростей набегающего на тело однородного потока со скоростью на бесконечности V¥, направленной параллельно оси Оу (Приложение 1, б).
Полагая в только что выведенной общей формуле потенциала
An1 = сV¥Сn, An2 = An3 =… = 0, Bn1 = Вn2 =… = 0,
т.е. довольствуясь решением, содержащим cos e, и, кроме того, представляя у по формулам, помещенным в начале § 1, как функцию l, m и e
![]()
получим следующее выражение потенциала скоростей поперечно набегающего со скоростью V¥ вдоль оси Оу потока:
![]()
или, используя определение присоединенных функций Лежандра (14),
![]() (15)
(15)
Для определения постоянных Сn, как и ранее, следует составить граничное условие на заданной поверхности обтекаемого тела. В этом случае неосесимметричного движения функция тока отсутствует и приходится непосредственно вычислять нормальную скорость Vn = ¶j/¶n и приравнивать ее нулю.
Несколько облегчая вычисления, выпишу в выбранной системе координат (l, m) условие, что при непроницаемости поверхности обтекаемого тела элемент дуги его меридианного сечения параллелен составляющей скорости в меридианной плоскости (условие скольжения жидкости по поверхности тела):
![]()
или, вспоминая выражения элементов дуг координатных линий и проекций градиента потенциала на направления этих линий,
![]()
Отсюда вытекает искомое граничное условие
![]() (16)
(16)
в котором l является заданной функцией m согласно уравнению контура обтекаемого тела в меридиональной плоскости. Составляя частные производные ¶j/¶l, ¶j/¶m и используя (15) получаю:
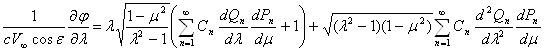
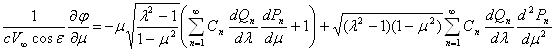
Заменив входящие сюда выражения вторых производных на основании дифференциальных уравнений функций Рn и Qn
![]()
получим после простых приведений
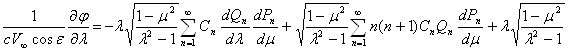
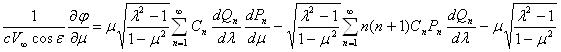
Подставляя эти выражения производных в (16) и используя ранее выведенные значения коэффициентов Ламе
![]()
получим после очевидных сокращений
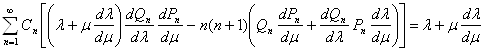
Имея в виду, что на поверхности тела l представляет заданную функцию от m, перепишем граничное условие в окончательной форме так:
![]() (17)
(17)
Похожие работы
... и трещинами. Решение построено на использовании теории функции комплексного переменного и удовлетворении граничным условиям методом наименьших квадратов. 1 Термодинамические основы термоупругости 1.1 Термоупругость Основное уравнение термоупругости. При термическом расширении изотропное тело деформируется таким образом, что компоненты деформации отнесенные к системе прямоугольных осей ...
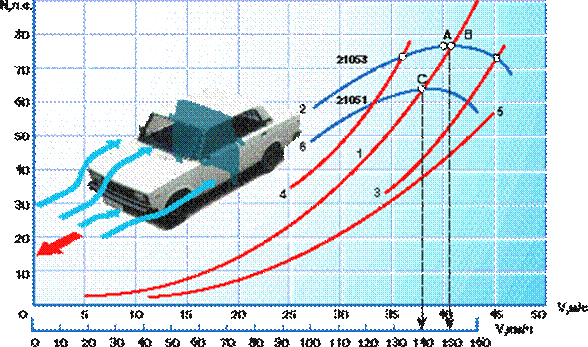
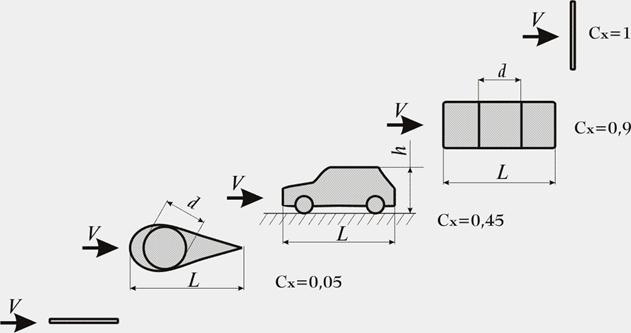
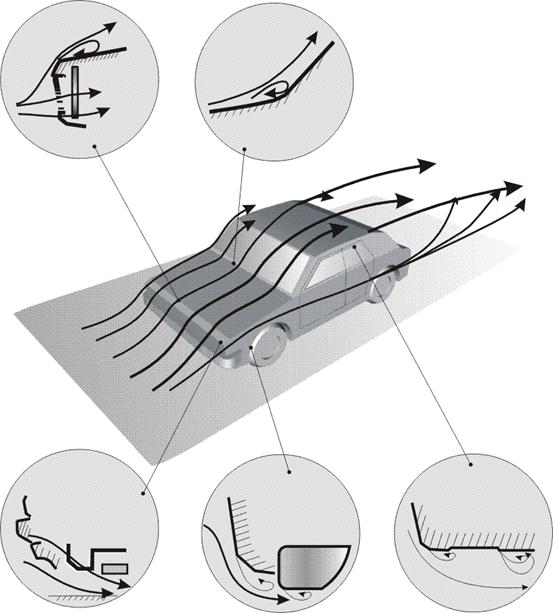
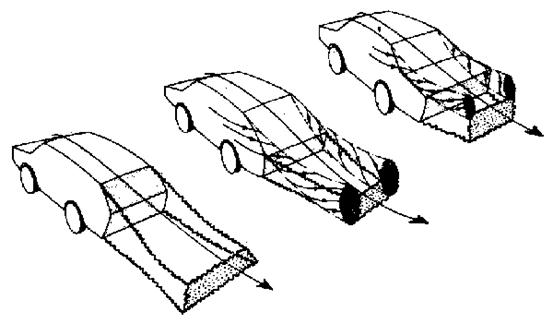
... увеличении скорости движения транспортного средства в два раза, сила сопротивления воздуха увеличивается в четыре раза, а затраты мощности вырастают в восемь раз!!! Поэтому при движении автомобиля в городском потоке аэродинамическое сопротивление автомобиля мало, на трассе же его значение достигает больших величин. А что говорить о гоночных болидах, движущихся со скоростями 300 км/час. В таких ...
... ребрами) изображают конструктивные и потоковые функциональные структуры [14]. Принципы построения функциональных структур технических объектов рассматриваются в последующих главах курса "Основы проектирования им конструирования" не включенных в настоящее пособие. Для систем управления существуют характеристики, которые можно использовать в качестве критериев для оценки структур. Одна из них - ...
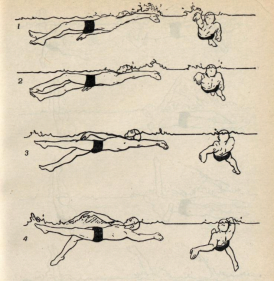
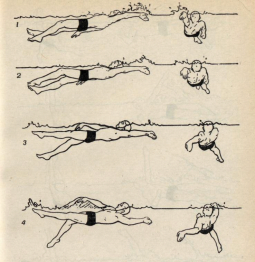
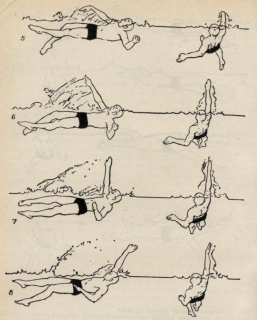
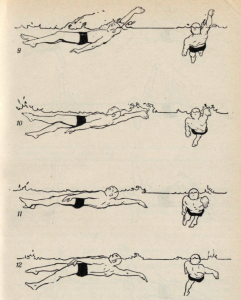
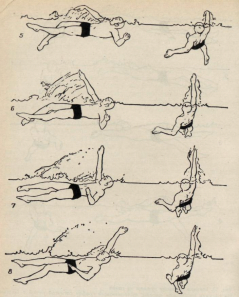
... - выдох (через нос или через рот и нос одновременно). Следует осуществлять полный выдох, который является необходимым условием для последующего полного вдоха. [1] 3. Биокинематическая схема плавания способом "кроль на спине" На рисунке 1 изображен пловец, выполняющий гребок согнутой рукой с шестью ударами ног на каждый цикл движений рук. Для определения глубины гребка рукой смотри вид сбоку. ...









0 комментариев