Навигация
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
Учреждение образования
"Гомельский государственный университет
имени Франциска Скорины"
математический факультет
Кафедра алгебры и геометрии
Произведение двух групп
Курсовая работа
Исполнитель:
студентка группы H.01.01.01 М-31
Закревская С.А.
Научный руководитель:
доктор физико-математических наук,
профессор кафедры Алгебры и геометрии
Монахов В. С.
Гомель 2005
Содержание
Введение
![]() 1 О произведении двух групп, одна из которых содержит циклическую подгруппу индекса
1 О произведении двух групп, одна из которых содержит циклическую подгруппу индекса ![]()
![]() 2 О произведении двух групп с циклическими подгруппами индекса 2
2 О произведении двух групп с циклическими подгруппами индекса 2
![]() 3 Произведение разрешимой и циклической групп
3 Произведение разрешимой и циклической групп
![]() 3.1. Вспомогательные результаты
3.1. Вспомогательные результаты
![]() 3.2. Доказательства теорем 1 и 2
3.2. Доказательства теорем 1 и 2
Заключение
Список литературы
Введение
Данную работу можно рассматривать как продолжение трудов Б. Хупперта и В. Скотта. В ней приводятся свойства конечных групп, являющихся произведением двух групп, а именно являющихся произведением двух групп, одна из которых содержит циклическую подгруппу индекса ![]() , произведением двух групп с циклическими подгруппами индекса 2, произведением разрешимой и циклической групп.
, произведением двух групп с циклическими подгруппами индекса 2, произведением разрешимой и циклической групп.
Рассматриваются вопросы разрешимости, сверхразрешимости и изоморфизма конечных групп, с приведенными выше свойствами и приводится описание двух классов неразрешимых факторизуемых групп. Так же приводятся доказательства следующих теорем:
Теорема 1.1 . Если ![]() и
и ![]() - группы с циклическими подгруппами индексов
- группы с циклическими подгруппами индексов ![]() , то конечная группа
, то конечная группа ![]() разрешима.
разрешима.
Теорема 1.2 . Пусть ![]() - группа Шмидта, а
- группа Шмидта, а ![]() - группа с циклической подгруппой индекса
- группа с циклической подгруппой индекса ![]() . Если
. Если ![]() и
и ![]() - конечная неразрешимая группа, то
- конечная неразрешимая группа, то ![]() изоморфна подгруппе
изоморфна подгруппе ![]() , содержащей
, содержащей ![]() , для подходящего
, для подходящего ![]() .
.
Теорема 1.3 . Пусть ![]() - 2-разложимая группа, а группа
- 2-разложимая группа, а группа ![]() имеет циклическую инвариантную подгруппу нечетного порядка и индекса 4. Если
имеет циклическую инвариантную подгруппу нечетного порядка и индекса 4. Если ![]() и
и ![]() - конечная неразрешимая группа, то
- конечная неразрешимая группа, то ![]() изоморфна подгруппе
изоморфна подгруппе ![]() , содержащей
, содержащей ![]() , для подходящего
, для подходящего ![]() .
.
Теорема 2.1 . Пусть конечная группа ![]() , где
, где ![]() и
и ![]() - группы с циклическими подгруппами индексов
- группы с циклическими подгруппами индексов ![]() . Тогда
. Тогда ![]() разрешима,
разрешима, ![]() и
и ![]() для любого простого нечетного
для любого простого нечетного ![]() .
.
Теорема 2.2 . Если группы ![]() и
и ![]() содержат циклические подгруппы нечетных порядков и индексов
содержат циклические подгруппы нечетных порядков и индексов ![]() , то конечная группа
, то конечная группа ![]() сверхразрешима.
сверхразрешима.
Теорема 2.3 . Пусть конечная группа ![]() , где
, где ![]() - циклическая подгруппа нечетного порядка, а подгруппа
- циклическая подгруппа нечетного порядка, а подгруппа ![]() содержит циклическую подгруппу индекса
содержит циклическую подгруппу индекса ![]() . Если в
. Если в ![]() нет нормальных секций, изоморфных
нет нормальных секций, изоморфных ![]() , то
, то ![]() сверхразрешима.
сверхразрешима.
Теорема 3.1 . Пусть конечная группа ![]() является произведением разрешимой подгруппы
является произведением разрешимой подгруппы ![]() и циклической подгруппы
и циклической подгруппы ![]() и пусть
и пусть ![]() . Тогда
. Тогда ![]() , где
, где ![]() - нормальная в
- нормальная в ![]() подгруппа,
подгруппа, ![]() и
и ![]() или
или ![]() для подходящего
для подходящего ![]() .
.
Теорема 3.2 . Конечная группа, являющаяся произведением 2-нильпотентной подгруппы и циклической подгруппы, непроста. Если циклический фактор имеет нечетный порядок, то группа разрешима.
Теорема 3.3 . Если ![]() - простая группа, где
- простая группа, где ![]() - холловская собственная в
- холловская собственная в ![]() подгруппа, а
подгруппа, а ![]() - абелева
- абелева ![]() -группа, то
-группа, то ![]() есть расширение группы, изоморфной секции из
есть расширение группы, изоморфной секции из ![]() , с помощью элементарной абелевой 2-группы. В частности, если
, с помощью элементарной абелевой 2-группы. В частности, если ![]() циклическая, то
циклическая, то ![]() есть расширение абелевой группы с помощью элементарной абелевой 2-группы.
есть расширение абелевой группы с помощью элементарной абелевой 2-группы.
![]() 1. О произведении двух групп, одна из которых содержит циклическую подгруппу индекса
1. О произведении двух групп, одна из которых содержит циклическую подгруппу индекса ![]()
Доказывается, что конечная группа ![]() разрешима, если группы
разрешима, если группы ![]() и
и ![]() содержат циклические подгруппы индексов
содержат циклические подгруппы индексов ![]() . Приводится описание двух классов неразрешимых факторизуемых групп. Библ. 18 назв.
. Приводится описание двух классов неразрешимых факторизуемых групп. Библ. 18 назв.
В работе Б. Хупперт установил разрешимость конечной группы, которая является произведением двух диэдральных подгрупп. В. Скотт получил разрешимость группы ![]() , допустив в качестве множителей
, допустив в качестве множителей ![]() и
и ![]() еще так называемые дициклические группы. Диэдральные и дициклические группы содержат циклические подгруппы индекса 2, но не исчерпывают весь класс групп с циклическими подгруппами индекса 2. В настоящей заметке доказана
еще так называемые дициклические группы. Диэдральные и дициклические группы содержат циклические подгруппы индекса 2, но не исчерпывают весь класс групп с циклическими подгруппами индекса 2. В настоящей заметке доказана
Теорема 1 . Если ![]() и
и ![]() - группы с циклическими подгруппами индексов
- группы с циклическими подгруппами индексов ![]() , то конечная группа
, то конечная группа ![]() разрешима.
разрешима.
Если подгруппа ![]() нильпотентна, а в
нильпотентна, а в ![]() есть циклическая подгруппа индекса 2, то, как показали H. Ито и Б. Хупперт, конечная группа
есть циклическая подгруппа индекса 2, то, как показали H. Ито и Б. Хупперт, конечная группа ![]() разрешима. Дополнением этого результата являются теоремы 2 и 3.
разрешима. Дополнением этого результата являются теоремы 2 и 3.
Теорема 2 . Пусть ![]() - группа Шмидта, а
- группа Шмидта, а ![]() - группа с циклической подгруппой индекса
- группа с циклической подгруппой индекса ![]() . Если
. Если ![]() и
и ![]() - конечная неразрешимая группа, то
- конечная неразрешимая группа, то ![]() изоморфна подгруппе
изоморфна подгруппе ![]() , содержащей
, содержащей ![]() , для подходящего
, для подходящего ![]() .
.
![]() обозначает наибольшую разрешимую инвариантную в
обозначает наибольшую разрешимую инвариантную в ![]() подгруппу. Группой Шмидта называется ненильпотентная группа, все собственные подгруппы которой нильпотентны.
подгруппу. Группой Шмидта называется ненильпотентная группа, все собственные подгруппы которой нильпотентны.
Теорема 3 . Пусть ![]() - 2-разложимая группа, а группа
- 2-разложимая группа, а группа ![]() имеет циклическую инвариантную подгруппу нечетного порядка и индекса 4. Если
имеет циклическую инвариантную подгруппу нечетного порядка и индекса 4. Если ![]() и
и ![]() - конечная неразрешимая группа, то
- конечная неразрешимая группа, то ![]() изоморфна подгруппе
изоморфна подгруппе ![]() , содержащей
, содержащей ![]() , для подходящего
, для подходящего ![]() .
.
Частным случаем теоремы 3, когда ![]() - абелева, а
- абелева, а ![]() имеет порядок
имеет порядок ![]() ,
, ![]() - простое число, является теорема 8 Б. Хупперта.
- простое число, является теорема 8 Б. Хупперта.
Доказательства теорем 1--3 и составляют содержание настоящей заметки.
Рассматриваются только конечные группы. Все используемые определения и обозначения стандартны, их можно найти в обзоре С. А. Чунихина и Л. А. Шеметкова.
Вначале докажем несколько лемм.
Лемма 1 . Пусть в группе существует циклическая подгруппа индекса ![]() . Тогда каждая подгруппа и фактор-группа обладает, циклической подгруппой индекса
. Тогда каждая подгруппа и фактор-группа обладает, циклической подгруппой индекса ![]() . Доказательство осуществляется непосредственной проверкой.
. Доказательство осуществляется непосредственной проверкой.
Лемма 2 . Пусть ![]() ,
, ![]() - собственная подгруппа группы
- собственная подгруппа группы ![]() ,
, ![]() - подгруппа четного порядка с циклической силовской 2-подгруппой. Если
- подгруппа четного порядка с циклической силовской 2-подгруппой. Если ![]() , то
, то ![]() содержит подгруппу индекса 2.
содержит подгруппу индекса 2.
Доказательство. Если ![]() содержит инвариантную в
содержит инвариантную в ![]() подгруппу
подгруппу ![]() , то фактор-группа
, то фактор-группа ![]() удовлетворяет условиям леммы. По индукции
удовлетворяет условиям леммы. По индукции ![]() обладает подгруппой индекса 2, поэтому и в
обладает подгруппой индекса 2, поэтому и в ![]() есть подгруппа индекса 2.
есть подгруппа индекса 2.
Пусть ![]() не содержит инвариантных в
не содержит инвариантных в ![]() подгрупп
подгрупп ![]() . Тогда представление группы
. Тогда представление группы ![]() подстановками правых смежных классов по
подстановками правых смежных классов по ![]() есть точное степени
есть точное степени ![]() , где
, где ![]() . Группу
. Группу ![]() можно отождествить с ее образом в симметрической группе
можно отождествить с ее образом в симметрической группе ![]() степени
степени ![]() . Так как в
. Так как в ![]() силовская 2-подгруппа
силовская 2-подгруппа ![]() циклическая, то
циклическая, то ![]() , где
, где ![]() - инвариантное 2-дополнение. Пусть
- инвариантное 2-дополнение. Пусть ![]() ,
, ![]() .
. ![]() ,
, ![]() и
и ![]() . Подстановка
. Подстановка ![]() разлагается в произведение циклов
разлагается в произведение циклов
![]()
т. е. подстановка ![]() имеет
имеет ![]() циклов, каждый длины
циклов, каждый длины ![]() . Декремент подстановки равен
. Декремент подстановки равен ![]() и есть нечетное число, поэтому
и есть нечетное число, поэтому ![]() - нечетная подстановка. Теперь
- нечетная подстановка. Теперь ![]() , а так как индекс
, а так как индекс ![]() в
в ![]() равен 2, то
равен 2, то ![]() - подгруппа индекса 2 в группе
- подгруппа индекса 2 в группе ![]() .
.
Лемма 2 обобщает лемму А. В. Романовского.
Замечание. Простая группа ![]() является произведением двух подгрупп
является произведением двух подгрупп ![]() и
и ![]() , причем
, причем ![]() , а
, а ![]() - группа порядка
- группа порядка ![]() с циклической силовской 2-подгруппой. Этот пример показывает, что требование
с циклической силовской 2-подгруппой. Этот пример показывает, что требование ![]() отбросить нельзя.
отбросить нельзя.
Лемма 3 . Пусть ![]() - дважды транзитивная группа подстановок на множестве
- дважды транзитивная группа подстановок на множестве ![]() и пусть
и пусть ![]() - стабилизатор некоторой точки
- стабилизатор некоторой точки ![]() . Тогда все инволюции из центра
. Тогда все инволюции из центра ![]() содержатся в
содержатся в ![]() .
.
Доказательство. Пусть ![]() . Допустим, что существует
. Допустим, что существует ![]() , причем
, причем ![]() . Так как
. Так как ![]() транзитивна на
транзитивна на ![]() , то
, то ![]() . Ho
. Ho ![]() , поэтому
, поэтому ![]() и
и ![]() - тождественная подстановка. Противоречие. Следовательно,
- тождественная подстановка. Противоречие. Следовательно, ![]() фиксирует только
фиксирует только ![]() . Теперь подстановка
. Теперь подстановка ![]() содержит только один цикл длины 1, а так как
содержит только один цикл длины 1, а так как ![]() - инволюция, то
- инволюция, то ![]() нечетен. Но
нечетен. Но ![]() , поэтому существует силовская 2-подгруппа
, поэтому существует силовская 2-подгруппа ![]() из
из ![]() с
с ![]() и
и ![]() . Если
. Если ![]() , то
, то ![]() , отсюда
, отсюда ![]() и
и ![]() , т. е.
, т. е. ![]() . Теперь
. Теперь ![]() и из теоремы Глаубермана следует, что
и из теоремы Глаубермана следует, что ![]() .
.
Лемма 4 . Пусть центр группы ![]() имеет четный порядок и силовская 2-подгруппа из
имеет четный порядок и силовская 2-подгруппа из ![]() либо циклическая, либо инвариантна в
либо циклическая, либо инвариантна в ![]() . Если
. Если ![]() - группа с циклической подгруппой индекса
- группа с циклической подгруппой индекса ![]() , то группа
, то группа ![]() непроста.
непроста.
Доказательство. Пусть ![]() - циклическая подгруппа в
- циклическая подгруппа в ![]() , для которой
, для которой ![]() , а
, а ![]() - максимальная в
- максимальная в ![]() подгруппа, содержащая
подгруппа, содержащая ![]() . Тогда
. Тогда ![]() . Если
. Если ![]() , то
, то ![]() и по лемме С. А. Чунихина группа
и по лемме С. А. Чунихина группа ![]() непроста. Значит,
непроста. Значит, ![]() .
.
Допустим, что порядок ![]() нечетен. Если
нечетен. Если ![]() , то
, то ![]() . Если
. Если ![]() , то ввиду леммы 2
, то ввиду леммы 2 ![]() и поэтому опять
и поэтому опять ![]() . Рассмотрим представление
. Рассмотрим представление ![]() подстановками смежных классов по
подстановками смежных классов по ![]() . Так как
. Так как ![]() - максимальная в
- максимальная в ![]() подгруппа, то
подгруппа, то ![]() - примитивная группа подстановок степени
- примитивная группа подстановок степени ![]() . Если
. Если ![]() - простое число, то
- простое число, то ![]() либо разрешима, либо дважды транзитивна. Если
либо разрешима, либо дважды транзитивна. Если ![]() - составное число, то, так как
- составное число, то, так как ![]() - регулярная группа подстановок при этом представлении,
- регулярная группа подстановок при этом представлении, ![]() - опять дважды транзитивна. Из леммы 3 следует, что
- опять дважды транзитивна. Из леммы 3 следует, что ![]() непроста.
непроста.
Пусть порядок ![]() четен. Если
четен. Если ![]() , то
, то ![]() непроста по лемме 2. Значит,
непроста по лемме 2. Значит, ![]() и
и ![]() . Пусть
. Пусть ![]() - силовская 2-подгруппа из
- силовская 2-подгруппа из ![]() . Если
. Если ![]() инвариантна в
инвариантна в ![]() , то
, то ![]() инвариантна и в
инвариантна и в ![]() . Следовательно,
. Следовательно, ![]() - циклическая группа. Но
- циклическая группа. Но ![]() не является силовской в
не является силовской в ![]() , поэтому
, поэтому ![]() содержится как подгруппа индекса 2 в некоторой группе
содержится как подгруппа индекса 2 в некоторой группе ![]() . Теперь для инволюции
. Теперь для инволюции ![]() из центра
из центра ![]() имеем
имеем ![]() , т. е.
, т. е. ![]() не максимальная в
не максимальная в ![]() . Противоречие.
. Противоречие.
Следствие. Пусть группа ![]() , где группа
, где группа ![]() содержит циклическую подгруппу индекса
содержит циклическую подгруппу индекса ![]() . Если
. Если ![]() - 2-разложимая группа четного порядка, то группа
- 2-разложимая группа четного порядка, то группа ![]() непроста.
непроста.
Лемма 5 . Пусть группа ![]() содержит циклическую инвариантную подгруппу нечетного порядка и индекса 2. Если
содержит циклическую инвариантную подгруппу нечетного порядка и индекса 2. Если ![]() - 2-разложимая группа, то группа
- 2-разложимая группа, то группа ![]() разрешима.
разрешима.
Доказательство. Применим индукцию к порядку ![]() . Если
. Если ![]() , то ввиду леммы 1 фактор-группа
, то ввиду леммы 1 фактор-группа ![]() удовлетворяет условиям леммы. По индукции,
удовлетворяет условиям леммы. По индукции, ![]() разрешима, отсюда разрешима и
разрешима, отсюда разрешима и ![]() .
.
Пусть ![]() . Если
. Если ![]() - циклическая, то
- циклическая, то ![]() разрешима по теореме В. А. Ведерникова. Поэтому
разрешима по теореме В. А. Ведерникова. Поэтому ![]() ,
, ![]() - циклическая подгруппа индекса 2,
- циклическая подгруппа индекса 2, ![]() . Пусть
. Пусть ![]() , где
, где ![]() - силовская 2-подгруппа из
- силовская 2-подгруппа из ![]() ,
, ![]() - ее дополнение. Если
- ее дополнение. Если ![]() , то
, то ![]() разрешима. Теперь
разрешима. Теперь ![]() и
и ![]() можно считать силовской 2-подгруппой в
можно считать силовской 2-подгруппой в ![]() . Так как
. Так как ![]() и
и ![]() , то
, то ![]() . Пусть
. Пусть ![]() и
и ![]() . Тогда
. Тогда ![]() и
и ![]() . По лемме С. А. Чунихина подгруппа
. По лемме С. А. Чунихина подгруппа ![]() максимальна в
максимальна в ![]() и
и ![]() . Представление группы
. Представление группы ![]() подстановками смежных классов по подгруппе
подстановками смежных классов по подгруппе ![]() дважды транзитивное: если
дважды транзитивное: если ![]() - простое число, если
- простое число, если ![]() - составное. Из леммы 3 вытекает теперь, что
- составное. Из леммы 3 вытекает теперь, что ![]() .Противоречие.
.Противоречие.
Доказательство теоремы 1 . Применим индукцию к порядку группы G. Пусть ![]() и
и ![]() - циклические инвариантные подгруппы в
- циклические инвариантные подгруппы в ![]() и в
и в ![]() соответственно, чьи индексы равны 1 или 2, а
соответственно, чьи индексы равны 1 или 2, а ![]() и
и ![]() - те силовские 2-подгруппы из
- те силовские 2-подгруппы из ![]() и
и ![]() , для которых
, для которых ![]() и
и ![]() есть силовская 2-подгруппа
есть силовская 2-подгруппа ![]() . Будем считать, что
. Будем считать, что ![]() . Если
. Если ![]() , то
, то ![]() и
и ![]() разрешима по теореме Ито-Хупперта. Поэтому в дальнейшем полагаем, что
разрешима по теореме Ито-Хупперта. Поэтому в дальнейшем полагаем, что ![]() . Ввиду леммы 1 каждая фактор-группа удовлетворяет условиям теоремы, поэтому
. Ввиду леммы 1 каждая фактор-группа удовлетворяет условиям теоремы, поэтому ![]()
Допустим, что ![]() . Если
. Если ![]() , то
, то ![]() и
и ![]() . Так как
. Так как ![]() разрешима, то
разрешима, то ![]() . Если
. Если ![]() , то
, то ![]() и
и ![]() разрешима.
разрешима.
Пусть теперь ![]() . Тогда и
. Тогда и ![]() . Так как
. Так как ![]() не является силовской подгруппой в
не является силовской подгруппой в ![]() , то
, то ![]() содержится как подгруппа индекса 2 в некоторой 2-группе
содержится как подгруппа индекса 2 в некоторой 2-группе ![]() . Обозначим через
. Обозначим через ![]() силовскую 2-подгруппу из
силовскую 2-подгруппу из ![]() . Очевидно, что
. Очевидно, что ![]() инвариантна в
инвариантна в ![]() .
.
Предположим, что ![]() и пусть
и пусть ![]() - инволюция из
- инволюция из ![]() . В
. В ![]() все подгруппы характеристические и
все подгруппы характеристические и ![]() инвариантна в
инвариантна в ![]() , поэтому
, поэтому ![]() и
и ![]() . Пусть
. Пусть ![]() - максимальная в
- максимальная в ![]() подгруппа, которая содержит
подгруппа, которая содержит ![]() . Тогда
. Тогда ![]() разрешима по индукции. Если
разрешима по индукции. Если ![]() , то
, то ![]() содержится в
содержится в ![]() и
и ![]() . Значит,
. Значит, ![]() . Так как
. Так как ![]() - собственная в
- собственная в ![]() подгруппа, то
подгруппа, то ![]() ,
, ![]() и
и ![]() . Теперь
. Теперь ![]() - дважды транзитивная группа степени
- дважды транзитивная группа степени ![]() на множестве смежных классов по
на множестве смежных классов по ![]() : если
: если ![]() - простое число, то применимо утверждение из, стр. 609; если
- простое число, то применимо утверждение из, стр. 609; если ![]() составное. Из леммы 3 получаем, что
составное. Из леммы 3 получаем, что ![]() . Противоречие.
. Противоречие.
Следовательно, ![]() . Если
. Если ![]() , то
, то ![]() и
и ![]() .Так как
.Так как ![]() не содержит подгрупп, инвариантных в
не содержит подгрупп, инвариантных в ![]() , то представление группы
, то представление группы ![]() подстановками по подгруппе
подстановками по подгруппе ![]() - точное степени 4. Поэтому
- точное степени 4. Поэтому ![]() - группа диэдра порядка 8,
- группа диэдра порядка 8, ![]() и
и ![]() . В этом случае
. В этом случае ![]() неабелева. Напомним, что
неабелева. Напомним, что ![]() и
и ![]() . Таким образом, для силовской 2-подгруппы
. Таким образом, для силовской 2-подгруппы ![]() из
из ![]() имеем:
имеем: ![]() - группа порядка 4 или неабелева группа порядка 8 (если
- группа порядка 4 или неабелева группа порядка 8 (если ![]() ).
).
Предположим, что порядки групп ![]() и
и ![]() делятся одновременно на нечетное простое число
делятся одновременно на нечетное простое число ![]() и пусть
и пусть ![]() и
и ![]() - силовские
- силовские ![]() -подгруппы из
-подгруппы из ![]() и
и ![]() соответственно. Так как
соответственно. Так как ![]() инвариантна в
инвариантна в ![]() , a
, a ![]() инвариантна в
инвариантна в ![]() , то
, то ![]() и
и ![]() - силовская
- силовская ![]() -подгруппа в
-подгруппа в ![]() . Без ограничения общности можно считать, что
. Без ограничения общности можно считать, что ![]() . По теореме VI.10.1 из группа
. По теореме VI.10.1 из группа ![]() содержит неединичную подгруппу
содержит неединичную подгруппу ![]() , инвариантную в
, инвариантную в ![]() . Но теперь
. Но теперь ![]() и
и ![]() , а так как
, а так как ![]() инвариантна в
инвариантна в ![]() , a
, a ![]() разрешима, то
разрешима, то ![]() по лемме С. А. Чунихина. Противоречие. Следовательно, порядки
по лемме С. А. Чунихина. Противоречие. Следовательно, порядки ![]() и
и ![]() не имеют общих нечетных делителей. В частности, в группе
не имеют общих нечетных делителей. В частности, в группе ![]() силовские подгруппы для нечетных простых чисел циклические.
силовские подгруппы для нечетных простых чисел циклические.
Пусть ![]() - минимальная инвариантная в
- минимальная инвариантная в ![]() подгруппа и
подгруппа и ![]() - силовская 2-подгруппа из
- силовская 2-подгруппа из ![]() , которая содержится в
, которая содержится в ![]() . Так как
. Так как ![]() , то
, то ![]() неразрешима и
неразрешима и ![]() . Подгруппа
. Подгруппа ![]() даже простая потому, что силовские подгруппы по нечетным простым числам циклические.
даже простая потому, что силовские подгруппы по нечетным простым числам циклические.
Пусть вначале ![]() . Тогда
. Тогда ![]() и
и ![]() неабелева. По теореме П. Фонга из группа
неабелева. По теореме П. Фонга из группа ![]() диэдральная или полудиэдральная. Но в этих случаях
диэдральная или полудиэдральная. Но в этих случаях ![]() . Непосредственно проверяется, что диэдральная и полудиэдральная группа порядка 16 не является произведением двух групп порядка 4.
. Непосредственно проверяется, что диэдральная и полудиэдральная группа порядка 16 не является произведением двух групп порядка 4.
Предположим теперь что ![]() . Тогда
. Тогда ![]() - элементарная абелева подгруппа или диэдральная. Если
- элементарная абелева подгруппа или диэдральная. Если ![]() абелева, то
абелева, то ![]() или группа Янко
или группа Янко ![]() порядка 175560. Так как
порядка 175560. Так как ![]() неабелева, то
неабелева, то ![]() и индекс
и индекс ![]() в
в ![]() четен. Группа
четен. Группа ![]() разрешима, поэтому
разрешима, поэтому ![]() и
и ![]() или
или ![]() . Ho
. Ho ![]() группа порядка 3, a
группа порядка 3, a ![]() . Противоречие. Если
. Противоречие. Если ![]() - диэдральная группа порядка 8, то
- диэдральная группа порядка 8, то ![]() - нечетное простое число или
- нечетное простое число или ![]() . Но группы
. Но группы ![]() и
и ![]() не допускают нужной факторизации, поэтому
не допускают нужной факторизации, поэтому ![]() - собственная в
- собственная в ![]() подгруппа. Теперь
подгруппа. Теперь ![]() или
или ![]() . Если
. Если ![]() , то
, то ![]() - диэдральная группа порядка 16, а так как
- диэдральная группа порядка 16, а так как ![]() , то
, то ![]() . Противоречие. Если
. Противоречие. Если ![]() , то
, то ![]() и в
и в ![]() существует подгруппа порядка
существует подгруппа порядка ![]() или
или ![]() .
.
Пусть, наконец, ![]() . Тогда
. Тогда ![]() и
и ![]() . Так как фактор-группа
. Так как фактор-группа ![]() разрешима по индукции, то
разрешима по индукции, то ![]() и
и ![]() . Используя самоцентрализуемость силовской
. Используя самоцентрализуемость силовской ![]() -подгруппы в
-подгруппы в ![]() , нетрудно показать, что
, нетрудно показать, что ![]() не допускает требуемой факторизации. Теорема доказана.
не допускает требуемой факторизации. Теорема доказана.
Доказательство теоремы 2 . Допустим, что теорема неверна и группа ![]() - контрпример минимального порядка. Фактор-группа группы Шмидта есть либо группа Шмидта, либо циклическая
- контрпример минимального порядка. Фактор-группа группы Шмидта есть либо группа Шмидта, либо циклическая ![]() -группа. Поэтому в силу индукции и теоремы 1 мы можем считать, что
-группа. Поэтому в силу индукции и теоремы 1 мы можем считать, что ![]() . Пусть
. Пусть ![]() - произвольная минимальная инвариантная в
- произвольная минимальная инвариантная в ![]() подгруппа. Если
подгруппа. Если ![]() , то
, то ![]() , а так как
, а так как ![]() - нильпотентная группа, то
- нильпотентная группа, то ![]() разрешима по теореме Ито--Хупперта или по теореме Виландта--Кегеля. Отсюда разрешима и
разрешима по теореме Ито--Хупперта или по теореме Виландта--Кегеля. Отсюда разрешима и ![]() . Противоречие. Значит,
. Противоречие. Значит, ![]() , в частности,
, в частности, ![]() разрешима. Допустим, что
разрешима. Допустим, что ![]() . Тогда
. Тогда ![]() и
и ![]() удовлетворяет условиям леммы. Поэтому
удовлетворяет условиям леммы. Поэтому ![]() изоморфна подгруппе группы
изоморфна подгруппе группы ![]() , содержащей
, содержащей ![]() для подходящего
для подходящего ![]() . Так как
. Так как ![]() есть прямое произведение изоморфных простых неабелевых групп, то
есть прямое произведение изоморфных простых неабелевых групп, то ![]() и
и ![]() . Отсюда
. Отсюда ![]() . Подгруппа
. Подгруппа ![]() инвариантна в
инвариантна в ![]() так как
так как ![]() , то
, то ![]() разрешима и
разрешима и ![]() . Теперь
. Теперь ![]() изоморфна некоторой группе автоморфизмов
изоморфна некоторой группе автоморфизмов ![]() , т. е.
, т. е. ![]() из заключения теоремы. Противоречие. Значит,
из заключения теоремы. Противоречие. Значит, ![]() .
.
Таким образом, если ![]() - произвольная инвариантная в
- произвольная инвариантная в ![]() подгруппа, то
подгруппа, то ![]() .
.
Пусть ![]() ,
, ![]() - инвариантная силовская
- инвариантная силовская ![]() -подгруппа,
-подгруппа, ![]() - силовская
- силовская ![]() -подгруппа. Через
-подгруппа. Через ![]() обозначим циклическую подгруппу в
обозначим циклическую подгруппу в ![]() , для которой
, для которой ![]() . Допустим, что
. Допустим, что ![]() . В этом случае
. В этом случае ![]() и если
и если ![]() - подгруппа индекса 2 в
- подгруппа индекса 2 в ![]() , то
, то ![]() - циклическая подгруппа индекса 2 в
- циклическая подгруппа индекса 2 в ![]() . По теореме 1 группа
. По теореме 1 группа ![]() разрешима. Противоречие. Значит,
разрешима. Противоречие. Значит, ![]() . Теперь, если в
. Теперь, если в ![]() есть инвариантная подгруппа
есть инвариантная подгруппа ![]() четного индекса, то
четного индекса, то ![]() есть группа Шмидта с инвариантной силовской 2-подгруппой, что противоречит лемме 1.
есть группа Шмидта с инвариантной силовской 2-подгруппой, что противоречит лемме 1.
Следовательно, ![]() и в
и в ![]() нет инвариантных подгрупп четного индекса.
нет инвариантных подгрупп четного индекса.
Допустим, что ![]() , тогда
, тогда ![]() - группа нечетного порядка. Силовская 2-подгруппа
- группа нечетного порядка. Силовская 2-подгруппа ![]() из
из ![]() является силовской подгруппой в
является силовской подгруппой в ![]() и по результату В. Д. Мазурова группа
и по результату В. Д. Мазурова группа ![]() диэдральная или полудиэдральная. Если
диэдральная или полудиэдральная. Если ![]() диэдральная, то по теореме 16.3 группа
диэдральная, то по теореме 16.3 группа ![]() изоморфна
изоморфна ![]() или подгруппе группы
или подгруппе группы ![]() . Так как
. Так как ![]() не допускает требуемой факторизации, то
не допускает требуемой факторизации, то ![]() следует из заключения теоремы. Противоречие. Значит,
следует из заключения теоремы. Противоречие. Значит, ![]() - полудиэдральная группа. Если
- полудиэдральная группа. Если ![]() - центральная инволюция из
- центральная инволюция из ![]() , то
, то ![]() , поэтому
, поэтому ![]() и
и ![]() разрешима. По теореме Мазурова группа
разрешима. По теореме Мазурова группа ![]() изоморфна
изоморфна ![]() или
или ![]() . Нетрудно проверить, что
. Нетрудно проверить, что ![]() и
и ![]() не допускают требуемой факторизации. Значит,
не допускают требуемой факторизации. Значит, ![]() .
.
Пусть ![]() - максимальная в
- максимальная в ![]() подгруппа, содержащая
подгруппа, содержащая ![]() . Тогда, если
. Тогда, если ![]() , то
, то ![]() и
и ![]() содержит подгруппу
содержит подгруппу ![]() , инвариантную в
, инвариантную в ![]() по лемме Чунихина. В этом случае,
по лемме Чунихина. В этом случае, ![]() и
и ![]() . Противоречие. Следовательно,
. Противоречие. Следовательно, ![]() .
.
Допустим, что ![]() не является силовской 2-подгруппой в
не является силовской 2-подгруппой в ![]() . Тогда
. Тогда ![]() немаксимальна в
немаксимальна в ![]() , а так как
, а так как ![]() и
и ![]() , то по лемме 2 порядок
, то по лемме 2 порядок ![]() нечетен. Теперь
нечетен. Теперь ![]() и
и ![]() содержит подгруппу индекса 2. Противоречие.
содержит подгруппу индекса 2. Противоречие.
Таким образом, ![]() - силовская 2-подгруппа группы
- силовская 2-подгруппа группы ![]() . Теперь,
. Теперь, ![]() и
и ![]() - максимальная в
- максимальная в ![]() подгруппа. Представление подстановками смежных классов по
подгруппа. Представление подстановками смежных классов по ![]() дважды транзитивное и по лемме 3 порядок центра
дважды транзитивное и по лемме 3 порядок центра ![]() нечетен. Отсюда следует, что
нечетен. Отсюда следует, что ![]() - абелева группа.
- абелева группа.
Пусть ![]() - минимальная инвариантная в
- минимальная инвариантная в ![]() подгруппа. Группа
подгруппа. Группа ![]() не является
не является ![]() -группой, поэтому некоторая силовская в
-группой, поэтому некоторая силовская в ![]() подгруппа циклическая и
подгруппа циклическая и ![]() - простая группа. Теперь можно применить результат Уолтера. Так как и группе Янко и в группах типа
- простая группа. Теперь можно применить результат Уолтера. Так как и группе Янко и в группах типа ![]() и нормализатор силовской 2-подгруппы имеет порядок
и нормализатор силовской 2-подгруппы имеет порядок ![]() , a
, a ![]() , то
, то ![]() изоморфна
изоморфна ![]() , где
, где ![]() или
или ![]() . Фактор-группа
. Фактор-группа ![]() разрешима, поэтому
разрешима, поэтому ![]() и
и ![]() изоморфна некоторой группе автоморфизмов
изоморфна некоторой группе автоморфизмов ![]() , т. е.
, т. е. ![]() из заключения теоремы. Противоречие. Теорема доказана.
из заключения теоремы. Противоречие. Теорема доказана.
Доказательство теоремы 3 . Пусть группа ![]() - контрпример минимального порядка,
- контрпример минимального порядка, ![]() - циклическая подгруппа в
- циклическая подгруппа в ![]() и
и ![]() , где
, где ![]() . Пусть
. Пусть ![]() , где
, где ![]() - силовская 2-подгруппа
- силовская 2-подгруппа ![]() , а
, а ![]() - ее 2-дополнение в
- ее 2-дополнение в ![]() . Если
. Если ![]() - силовская 2-подгруппа
- силовская 2-подгруппа ![]() , то
, то ![]() и
и ![]() разрешима по теореме Ведерникова. Противоречие. Теперь
разрешима по теореме Ведерникова. Противоречие. Теперь ![]() можно считать силовской 2-подгруппой группы
можно считать силовской 2-подгруппой группы ![]() .
.
Предположим, что ![]() . Фактор-группа
. Фактор-группа ![]() и
и ![]() - 2-разложимая группа. Очевидно, что циклическая подгруппа
- 2-разложимая группа. Очевидно, что циклическая подгруппа ![]() нечетного порядка инвариантна в
нечетного порядка инвариантна в ![]() и ее индекс равен 1, 2 или 4. В первых двух случаях группа
и ее индекс равен 1, 2 или 4. В первых двух случаях группа ![]() разрешима по лемме 5, поэтому разрешима и
разрешима по лемме 5, поэтому разрешима и ![]() . Противоречие. Если индекс равен 4, то по индукции и учитывая, что
. Противоречие. Если индекс равен 4, то по индукции и учитывая, что ![]() , получаем: группа
, получаем: группа ![]() изоморфна подгруппе
изоморфна подгруппе ![]() , содержащей
, содержащей ![]() для некоторых
для некоторых ![]() . Противоречие. Следовательно, в
. Противоречие. Следовательно, в ![]() нет разрешимых инвариантных подгрупп, отличных от единицы.
нет разрешимых инвариантных подгрупп, отличных от единицы.
Теперь покажем, что силовская 2-подгруппа ![]() является диэдральной группой порядка 4 или 8. Если
является диэдральной группой порядка 4 или 8. Если ![]() , то
, то ![]() , и так как
, и так как ![]() неразрешима, то
неразрешима, то ![]() диэдральная. Пусть
диэдральная. Пусть ![]() не содержится в
не содержится в ![]() .
.
Предположим, что ![]() и пусть
и пусть ![]() , где
, где ![]() - инволюция из
- инволюция из ![]() . Теперь
. Теперь ![]() и
и ![]() . Пусть вначале
. Пусть вначале ![]() и
и ![]() максимальна в
максимальна в ![]() . Тогда
. Тогда ![]() - дважды транзитивная группа на множестве смежных классов по подгруппе
- дважды транзитивная группа на множестве смежных классов по подгруппе ![]() : если
: если ![]() - простое число; если
- простое число; если ![]() - непростое число. Из леммы 3 получаем, что
- непростое число. Из леммы 3 получаем, что ![]() . Противоречие. Пусть
. Противоречие. Пусть ![]() - максимальная в
- максимальная в ![]() подгруппа, которая содержит
подгруппа, которая содержит ![]() . Тогда
. Тогда ![]() и
и ![]() . Кроме того,
. Кроме того, ![]() . Пусть
. Пусть ![]() - минимальная инвариантная в
- минимальная инвариантная в ![]() подгруппа, которая содержится в
подгруппа, которая содержится в ![]() ,
, ![]() существует по лемме Чунихина, а так как
существует по лемме Чунихина, а так как ![]() , то
, то ![]() , а следовательно, и
, а следовательно, и ![]() неразрешимы. По индукции
неразрешимы. По индукции ![]() изоморфна подгруппе
изоморфна подгруппе ![]() , содержащей
, содержащей ![]() , для некоторых
, для некоторых ![]() . Все инвариантные в
. Все инвариантные в ![]() подгруппы неразрешимы, поэтому
подгруппы неразрешимы, поэтому ![]() , а так как
, а так как ![]() - минимальная инвариантная в
- минимальная инвариантная в ![]() подгруппа, то
подгруппа, то ![]() . B силу леммы 5
. B силу леммы 5 ![]() , поэтому
, поэтому ![]() разрешима. Но тогда
разрешима. Но тогда ![]() и
и ![]() изоморфна группе автоморфизмов группы
изоморфна группе автоморфизмов группы ![]() , т. е.
, т. е. ![]() из заключения теоремы. Противоречие.
из заключения теоремы. Противоречие.
Значит, ![]() , поэтому
, поэтому ![]() не содержит инвариантных в
не содержит инвариантных в ![]() подгрупп, отличных от 1. Следовательно, представление группы
подгрупп, отличных от 1. Следовательно, представление группы ![]() подстановками смежных классов по подгруппе
подстановками смежных классов по подгруппе ![]() точное степени 4. Отсюда группа
точное степени 4. Отсюда группа ![]() есть группа диэдра порядка 8.
есть группа диэдра порядка 8.
Таким образом, силовская 2-подгруппа ![]() в группе
в группе ![]() есть диэдральная группа порядка 4 или 8. По результату Горенштейна - Уолтера группа
есть диэдральная группа порядка 4 или 8. По результату Горенштейна - Уолтера группа ![]() изоморфна
изоморфна ![]() , или подгруппе группы
, или подгруппе группы ![]() . Так как
. Так как ![]() , не допускает требуемой факторизации, то группа
, не допускает требуемой факторизации, то группа ![]() - из заключения теоремы. Противоречие. Теорема доказана.
- из заключения теоремы. Противоречие. Теорема доказана.
В заключение отметим, что, используя технику доказательств теорем 1--3 и следствие леммы 4, можно получить описание неразрешимых групп ![]() при условии, что
при условии, что ![]() - 2-разложимая группа, а в группе
- 2-разложимая группа, а в группе ![]() существует циклическая подгруппа индекса
существует циклическая подгруппа индекса ![]() .
.
Похожие работы
... нужно самому вести рассказ вслед за ребенком, повторяя то, что он сказал, и обязательно, добавляя пропущенное. 3. Методика ознакомления с литературными произведениями детей младшего дошкольного возраста (до 3 лет) Если в задачах работы по развитию звуковой культуры речи в 1 младшей группе на первое место ставилось звукоподражание, то во 2 - эта работа над звукопроизношением с развитием ...
... результат работы(6), мы доказываем в настоящей заметке следующую теорему. Теорема Пусть конечная группа является произведением своих подгрупп и взаимно простых порядков, и пусть --- бипримарная группа, а --- 2-разложимая группа четного порядка. Предположим, что в есть неединичная циклическая силовская подгруппа . Тогда, если неразрешима, то изоморфна или . обозначает произведение ...
... , т.е. . Здесь обозначает матрицу, транспонированную к , где , а – величина, комплексно – сопряженная к . В этом параграфе мы покажем, что каждое представление конечной группы эквивалентно некоторому ее унитарному представлению и является мполне приводимым. Матрица называется эрмитовой, если , и положительно определенной, если для каждого ненулевого столбца . Следующая лемма тривиальна. ...
... тогда и только тогда, когда она разложима в произведение попарно перестановочных -подгрупп по разным простым 1.2.35 Т е о р е м а (Кегель [31] – Виландт [4]). Конечная группа, представимая в виде произведения некоторых своих попарно перестановочных нильпотентных подгрупп, разрешима. 1.2.36 Т е о р е м а. Пусть – некоторое множество простых чисел; – группа, факторизуемая подгруппами и где ...
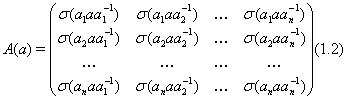

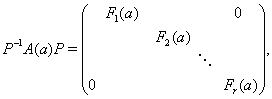

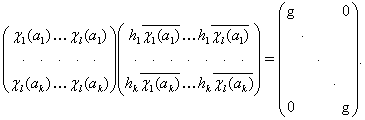
0 комментариев