Навигация
Произведение разрешимой и циклической групп
В настоящей заметке доказывается следующая
Теорема 1. Пусть конечная группа ![]() является произведением разрешимой подгруппы
является произведением разрешимой подгруппы ![]() и циклической подгруппы
и циклической подгруппы ![]() и пусть
и пусть ![]() . Тогда
. Тогда ![]() , где
, где ![]() - нормальная в
- нормальная в ![]() подгруппа,
подгруппа, ![]() и
и ![]() или
или ![]() для подходящего
для подходящего ![]() .
.
![]() означает произведение всех разрешимых нормальных в
означает произведение всех разрешимых нормальных в ![]() подгрупп.
подгрупп.
Следствие. Если простая группа ![]() является произведением разрешимой и циклической подгрупп, то
является произведением разрешимой и циклической подгрупп, то ![]() .
.
Несмотря на то, что среди ![]() при нечетном
при нечетном ![]() нет групп факторизуемых разрешимой подгруппой и циклической, группы
нет групп факторизуемых разрешимой подгруппой и циклической, группы ![]() допускают указанную факторизацию для каждого
допускают указанную факторизацию для каждого ![]() .
.
Из теоремы 1 вытекает
Теорема 2. Конечная группа, являющаяся произведением 2-нильпотентной подгруппы и циклической подгруппы, непроста. Если циклический фактор имеет нечетный порядок, то группа разрешима.
Работа состоит из двух параграфов. В первом параграфе приводятся необходимые вспомогательные результаты. Кроме того, доказывается теорема 3, которая является обобщением теоремы Виландта о разрешимости внешней группы автоморфизмов простой группы, содержащей подгруппу простого индекса. В ![]() 3.2 доказываются теоремы 1 и 2.
3.2 доказываются теоремы 1 и 2.
Все обозначения и определения стандартны. Запись ![]() означает, что конечная группа
означает, что конечная группа ![]() является произведением своих подгрупп
является произведением своих подгрупп ![]() и
и ![]() .
.
![]() 3.1 Вспомогательные результаты
3.1 Вспомогательные результаты
Пусть ![]() - подгруппа группы
- подгруппа группы ![]() . Тогда
. Тогда ![]() означает наибольшую нормальную в
означает наибольшую нормальную в ![]() подгруппу, которая содержится в
подгруппу, которая содержится в ![]() , a
, a ![]() - наименьшую нормальную в
- наименьшую нормальную в ![]() подгруппу, которая содержит
подгруппу, которая содержит ![]() .
.
Лемма 1. Если ![]() и
и ![]() содержит подгруппу
содержит подгруппу ![]() , нормальную в
, нормальную в ![]() , то
, то ![]() .
.
Лемма 2. Пусть ![]() и
и ![]() - нормальная в
- нормальная в ![]() подгруппа. Если
подгруппа. Если ![]() , то
, то ![]() .
.
Доказательство. Поскольку ![]() , то
, то ![]() . Так как
. Так как ![]() , то
, то ![]()
Лемма 3 . Если ![]() и
и ![]() абелева, то
абелева, то ![]() .
.
Доказательство. Пусть ![]() . Ясно, что
. Ясно, что ![]() и
и ![]() . Если
. Если ![]() , то
, то ![]() и
и ![]() . Таким образом,
. Таким образом, ![]() и
и ![]() .
.
Лемма 4 . Пусть ![]() и
и ![]() не делит
не делит ![]() . Тогда
. Тогда ![]() не сопряжен ни с одним элементом из
не сопряжен ни с одним элементом из ![]() .
.
Доказательство. Если ![]() , то
, то ![]() и
и ![]() делит
делит ![]() . Но
. Но ![]() по лемме VI.4.5 из, поэтому
по лемме VI.4.5 из, поэтому ![]() . Противоречие.
. Противоречие.
Лемма 5 . Пусть ![]() - минимальная нормальная подгруппа группы
- минимальная нормальная подгруппа группы ![]() и
и ![]() . Если
. Если ![]() разрешима, то
разрешима, то ![]() и
и ![]() изоморфна подгруппе из
изоморфна подгруппе из ![]() .
.
Доказательство. ![]() . Так как
. Так как ![]() разрешима, то
разрешима, то ![]() и
и ![]() . По лемме 1.4.5 из группа
. По лемме 1.4.5 из группа ![]() есть группа автоморфизмов
есть группа автоморфизмов ![]() .
.
Лемма 6 . Пусть ![]() , где
, где ![]() - собственная подгруппа
- собственная подгруппа ![]() , а
, а ![]() циклическая. Если
циклическая. Если ![]() , то справедливо одно из следующих утверждений:
, то справедливо одно из следующих утверждений:
1) ![]() и
и ![]() - нормализатор силовской 2-подгруппы, а
- нормализатор силовской 2-подгруппы, а ![]() ;
;
2) ![]() , а
, а ![]() ;
;
3) ![]() , а
, а ![]() .
.
Доказательство. См. теорему 0.8 из.
Лемма 7 . Группа ![]() при любом
при любом ![]() является произведением разрешимой подгруппы и циклической.
является произведением разрешимой подгруппы и циклической.
Доказательство. Если ![]() , то утверждение следует из леммы 6. Пусть
, то утверждение следует из леммы 6. Пусть ![]() , и
, и ![]() - силовская
- силовская ![]() -подгруппа в
-подгруппа в ![]() . Известно, что
. Известно, что ![]() циклическая и в
циклическая и в ![]() есть циклическая подгруппа
есть циклическая подгруппа ![]() порядка
порядка ![]() . Так как
. Так как ![]() и
и ![]() , то
, то ![]() .
.
Лемма 8 . Если ![]() , то
, то ![]() является произведением разрешимой и циклической подгрупп.
является произведением разрешимой и циклической подгрупп.
Доказательство. Известно, что ![]() , где
, где ![]() - циклическая группа порядка, делящего
- циклическая группа порядка, делящего ![]() , и
, и ![]() нормализует подгруппу
нормализует подгруппу ![]() , где
, где ![]() - силовская 2-подгруппа в
- силовская 2-подгруппа в ![]() . Так как
. Так как ![]() , где
, где ![]() - циклическая группа порядка
- циклическая группа порядка ![]() , то
, то ![]() и
и ![]() разрешима.
разрешима.
Лемма 9 . Группа ![]() является произведением разрешимой подгруппы и циклической. Группа
является произведением разрешимой подгруппы и циклической. Группа ![]() не допускает указанной факторизации.
не допускает указанной факторизации.
Доказательство. Группа ![]() имеет порядок
имеет порядок ![]() и в ней содержится подгруппа
и в ней содержится подгруппа ![]() индекса 2. Так как
индекса 2. Так как ![]() дважды транзитивна на множестве из 13 символов, то стабилизатор точки имеет порядок
дважды транзитивна на множестве из 13 символов, то стабилизатор точки имеет порядок ![]() и является разрешимой группой. Поэтому
и является разрешимой группой. Поэтому ![]() является произведением разрешимой подгруппы порядка
является произведением разрешимой подгруппы порядка ![]() и циклической подгруппы порядка 13.
и циклической подгруппы порядка 13.
Покажем, что ![]() не содержит подгруппы индекса 13. Допустим противное и пусть
не содержит подгруппы индекса 13. Допустим противное и пусть ![]() - подгруппа порядка
- подгруппа порядка ![]() . Так как
. Так как ![]() дважды транзитивна на смежных классах по
дважды транзитивна на смежных классах по ![]() , то центр
, то центр ![]() имеет нечетный порядок по лемме 2.2, а по лемме Берноайда
имеет нечетный порядок по лемме 2.2, а по лемме Берноайда ![]() , где
, где ![]() .
.
Пусть ![]() - подгруппа Фиттинга группы
- подгруппа Фиттинга группы ![]() , где
, где ![]() . Известно, что нормализатор силовской 3-подгруппы в
. Известно, что нормализатор силовской 3-подгруппы в ![]() имеет порядок
имеет порядок ![]() , поэтому
, поэтому ![]() . Так как
. Так как ![]() разрешима, то
разрешима, то ![]() и
и ![]() изоморфна подгруппе из
изоморфна подгруппе из ![]() .
.
Предположим, что ![]() . Тогда
. Тогда ![]() делит порядок
делит порядок ![]() , а значит и
, а значит и ![]() . Но это невозможно, так как
. Но это невозможно, так как ![]() . Противоречие.
. Противоречие.
Следовательно, ![]() . Далее
. Далее ![]() , так как
, так как ![]() - подгруппа нечетного порядка, поэтому
- подгруппа нечетного порядка, поэтому ![]() . Ясно, что
. Ясно, что ![]() , a
, a ![]() и
и ![]() . Силовская 2-подгруппа
. Силовская 2-подгруппа ![]() из
из ![]() является силовской в
является силовской в ![]() , значит, она полудиэдральная порядка 16, все инволюции сопряжены и централизатор каждой инволюции изоморфен
, значит, она полудиэдральная порядка 16, все инволюции сопряжены и централизатор каждой инволюции изоморфен ![]() порядка
порядка ![]() . Поэтому
. Поэтому ![]() .
. ![]() как подгруппа из
как подгруппа из ![]() полудиэдральна при
полудиэдральна при ![]() , либо циклическая, либо кватернионная, либо диэдральная порядка 4 или 8. В любом случае порядок
, либо циклическая, либо кватернионная, либо диэдральная порядка 4 или 8. В любом случае порядок ![]() не делится на 9. Таким образом,
не делится на 9. Таким образом, ![]() . Противоречие. Итак,
. Противоречие. Итак, ![]() не содержит подгруппы индекса 13.
не содержит подгруппы индекса 13.
Пусть ![]() , где
, где ![]() - разрешимая подгруппа, а
- разрешимая подгруппа, а ![]() - циклическая. В
- циклическая. В ![]() силовокие 13-подгруппы самоцентрализуемы, поэтому 13 делит порядок
силовокие 13-подгруппы самоцентрализуемы, поэтому 13 делит порядок ![]() . Так как в
. Так как в ![]() нет
нет ![]() - холловской подгруппы, то 3 делит порядок
- холловской подгруппы, то 3 делит порядок ![]() . Но в
. Но в ![]() силовская 3-подгруппа имеет экспоненту 3, поэтому в
силовская 3-подгруппа имеет экспоненту 3, поэтому в ![]() есть подгруппа
есть подгруппа ![]() порядка
порядка ![]() . Теперь силовская 13-подгруппа из
. Теперь силовская 13-подгруппа из ![]() не самоцентрализуема. Противоречие. Лемма 9 доказана.
не самоцентрализуема. Противоречие. Лемма 9 доказана.
Теорема 3 . Если ![]() - простая группа, где
- простая группа, где ![]() - холловская собственная в
- холловская собственная в ![]() подгруппа, а
подгруппа, а ![]() - абелева
- абелева ![]() -группа, то
-группа, то ![]() есть расширение группы, изоморфной секции из
есть расширение группы, изоморфной секции из ![]() , с помощью элементарной абелевой 2-группы. В частности, если
, с помощью элементарной абелевой 2-группы. В частности, если ![]() циклическая, то
циклическая, то ![]() есть расширение абелевой группы с помощью элементарной абелевой 2-группы.
есть расширение абелевой группы с помощью элементарной абелевой 2-группы.
Доказательство. Из простоты ![]() и леммы Чунихина вытекает, что
и леммы Чунихина вытекает, что ![]() и
и ![]() максишльна в
максишльна в ![]() . Представление группы
. Представление группы ![]() перестановками на смежных классах подгруппы
перестановками на смежных классах подгруппы ![]() будет точным и дважды транзитивным, следовательно, есть подгруппа перестановок симметрической группы S степени, равной порядку
будет точным и дважды транзитивным, следовательно, есть подгруппа перестановок симметрической группы S степени, равной порядку ![]() . Так как
. Так как ![]() - регулярная и транзитивная группа и
- регулярная и транзитивная группа и ![]() , то
, то ![]() также транзитивна. Но
также транзитивна. Но ![]() по теореме 1.6.5, поэтому
по теореме 1.6.5, поэтому ![]() самоцентрализуема в
самоцентрализуема в ![]() .
.
Группа автоморфизмов ![]() , индуцированная элементами из
, индуцированная элементами из ![]() , называется группой подстановочных автоморфизмов. Очевидно
, называется группой подстановочных автоморфизмов. Очевидно ![]() , а по теореме 3 подгруппа
, а по теореме 3 подгруппа ![]() нормальна в
нормальна в ![]() и
и ![]() - элементарная абелева 2-группа.
- элементарная абелева 2-группа.
По лемме Фраттини ![]() , поэтому обозначив
, поэтому обозначив ![]() будем иметь
будем иметь ![]() . Так как
. Так как ![]() , то
, то ![]() изоморфна секции из
изоморфна секции из ![]() . В частности, если
. В частности, если ![]() циклическая, то
циклическая, то ![]() абелева и
абелева и ![]() есть расширение абелевой группы с помощью элементарной абелевой 2-группы.
есть расширение абелевой группы с помощью элементарной абелевой 2-группы.
Похожие работы
... нужно самому вести рассказ вслед за ребенком, повторяя то, что он сказал, и обязательно, добавляя пропущенное. 3. Методика ознакомления с литературными произведениями детей младшего дошкольного возраста (до 3 лет) Если в задачах работы по развитию звуковой культуры речи в 1 младшей группе на первое место ставилось звукоподражание, то во 2 - эта работа над звукопроизношением с развитием ...
... результат работы(6), мы доказываем в настоящей заметке следующую теорему. Теорема Пусть конечная группа является произведением своих подгрупп и взаимно простых порядков, и пусть --- бипримарная группа, а --- 2-разложимая группа четного порядка. Предположим, что в есть неединичная циклическая силовская подгруппа . Тогда, если неразрешима, то изоморфна или . обозначает произведение ...
... , т.е. . Здесь обозначает матрицу, транспонированную к , где , а – величина, комплексно – сопряженная к . В этом параграфе мы покажем, что каждое представление конечной группы эквивалентно некоторому ее унитарному представлению и является мполне приводимым. Матрица называется эрмитовой, если , и положительно определенной, если для каждого ненулевого столбца . Следующая лемма тривиальна. ...
... тогда и только тогда, когда она разложима в произведение попарно перестановочных -подгрупп по разным простым 1.2.35 Т е о р е м а (Кегель [31] – Виландт [4]). Конечная группа, представимая в виде произведения некоторых своих попарно перестановочных нильпотентных подгрупп, разрешима. 1.2.36 Т е о р е м а. Пусть – некоторое множество простых чисел; – группа, факторизуемая подгруппами и где ...
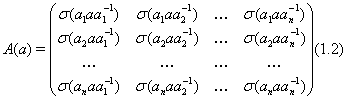


0 комментариев