Навигация
Доказательства теорем 1 и 2
39156
знаков
0
таблиц
0
изображений
3.2 Доказательства теорем 1 и 2 Доказательство теоремы 1 . Предположим, что теорема неверна и пусть 
- контрпример минимального порядка. Так как 
, то 
и 
по лемме 3.
Допустим, что 
не максимальна в и пусть 
- прямое произведение минимальных нормальных в подгрупп и 
- наибольшее. Очевидно, 
содержит все минимальные нормальные в подгруппы. Так как 
, то 
и 
. Поэтому изоморфна подгруппе из 
.
Допустим, что 
для некоторого 
. Тогда 
и 
разрешима. Значит, 
. Пусть 
- подгруппа в , собственно содержащая . Так как 
и 
- нормальная в 
неединичкая подгруппа, то 
. Теперь минимальная нормальная в подгруппа из 
совпадает с 
и 
, противоречие. Таким образом, 
для любого . По индукции 
изоморфна подгруппе 
, где 
- есть прямое произведение, построенное из групп 
. Очевидно, что 
, поэтому также есть прямое произведение, построенное из групп . Следовательно, обладает этим же свойством и - подгруппа из . Противоречие.
Итак, максимальна в . Поэтому представление перестановками на множестве смежных классов подгруппы будет точным и примитивным. Так как 
, то в этом представлении регулярна и дважды транзитивна. Пусть минимальная нормальная в подгруппа. Применяя теорему 11.3 и результат Берноайда, заключаем, что проста и примитивна, т.е. 
максимальна в . Так как 
, то 
разрешима и по лемме 5. Таким образом, изоморфна подгруппе из .
Предположим, что 
. Тогда 
неразрешима, 
и 
. Так как 
, то по индукции изоморфна подгруппе из , а 
или 
и из заключения теоремы. Следовательно, и 
по лемме 2.
Пусть порядок четен. Тогда содержит подгруппу индекса 2 по лемме 4.1. По теореме Хольта подгруппа 2-транзитивна и изоморфна 
- степень нечетного простого числа или группа типа Ри в их обычных 2-транзитивных представлениях. Если 
, то из заключения теоремы. Внешняя группа автоморфизмов группы типа Ри имеет нечетный порядок, поэтому не содержится в группе автоморфизмов группы типа Ри.
Пусть теперь изоморфна 
- простое нечетное число. Тогда 
, где 
и 
, где 
- силовская 
-подгруппа из и 
. Из леммы 2 получаем 
. Так как в 
все инволюции сопряжены и имеет четный порядок, то по лемме 4 подгруппа 
имеет нечетный порядок, в частности 
не делит 
.
Предположим, что существует простое число 
, делящее и 
. Если 
, то по лемме 2.5 порядок делит 
, а так как 
, то делит 
. Если 
, то делит и элементарные вычисления и применение леммы 2.5 показывают, что 
делит . Так как 
, то в любом случае 
. Известно, что 
, поэтому 
и 
. Противоречие с леммой 2.5.
Следовательно, не может быть изоморфна . Случай, когда порядок четен, рассмотрен полностью.
Пусть порядок подгруппы нечетен. Тогда 
содержит некоторую силовскую 2-подгруппу из . По теореме О'Нэна [??] подгруппа 
изоморфна 
или 
и 
нечетное число.
Пусть изоморфна 
.Тогда 
и делит 
. Поэтому содержит силовскую 2-подгруппу из и, используя информацию о подгруппах в 
, получаем, что 
делит 
, a 
делит 
или 
. Теперь делится на , которое делится на или на . Противоречие.
Пусть изоморфна 
. Так как имеет нечетный порядок, то силовская 2-подгруппа 
из содержится в . Если 
, то 
и по лемме 3.3 имеем 
. Если 
, то нормальна в , так как разрешимая группа с силовской 2-подгруппой имеет 2-длину 1. Итак, в любом случае . Но 
дважды транзитивна на смежных классах по 
, поэтому 
и нормальна в .
Поскольку и . Кроме того, 
, поэтому - нечетное число, делящее 
. Так как - циклическая группа нечетного порядка в , то либо делит , либо делит . Поэтому 
делится на , либо на . Очевидно, 
при 
. Случай 
исключается непосредственно. Следовательно, неизоморфна .
Предположим, что 
- нечетное и 
. Так как - стабилизатор точки и разрешима индекса , то 
, либо 
. Группа 
не допускает требуемой факторизации по лемме 9. Поэтому либо 
, либо 
. Теорема 1 доказана.
Доказательство теоремы 2 . Пусть 
- 2-нильпотентная группа и - ее силовская 2-подгруппа, - циклическая. Очевидно, мы можем считать, что . Пусть - максимальная в подгруппа, содержащая . Так как , то 
. Предположим, что 
. Тогда 
и группа непроста. Если порядок нечетен, то по индукции разрешима и 
, противоречие. Таким образом, 
, кроме того, 
максимальна в . Теперь - дважды транзитивна на множестве смежных классов по . Если порядок четен, то группа непроста по лемме 4.1. Пусть порядок нечетен. Тогда - силовская в подгруппа. По теореме Виландта-Кегеля 
, а по лемме 3.3 
и 
2-разложимая подгруппа. По теореме 1V.2.6 подгруппа неабелева. Так как из теоремы 1 в случае, когда порядок нечетен следует, что силовская 2-подгруппа в абелева, то имеем противоречие. Теорема доказана.
Симметрическая группа пяти символов факторизуется 2-нильпотентной подгруппой порядка 20 и циклической подгруппой порядка 6. Поэтому условие нечетности порядка циклического фактора существенно.
Заключение
В данной курсовой работе были приведены некоторые результаты, полученные Монаховым В. С. (Гомельская лаборатория института математики), проливающие свет на такие важные вопросы в теории конечных групп, как разрешимость и сверхразрешимость конечных групп, являющихся произведением двух групп с различными свойствами, а именно содержащих циклическую подгруппу индекса 
, содержащих циклические подгруппы индекса 2, разрешимые и циклические группы.
Эти полученные данные изложены в теоремах 1.1, 1.2, 1.3, 2.1, 2.2, 2.3, 3.1, 3.2 и 3.3. Так же представляют интерес данные изложенные в леммах, которые были использованы при доказательстве выше упомянутых теорем. В особенности следует выделить лемму 1.2, которая обобщает лемму А. В. Романоского и теорему 1.3, являющеюся обобщением теоремы Б. Хупперта.
Список использванных источников
1. Монахов В.С. О произведении двух групп, одна из которых содержит циклическую подгруппу индекса .// Математические заметки.-1974.-Т.16, №2-с. 285-295
2. Монахов В.С. Произведение разрешимой и циклической групп// Сб. VI всес. симпозиум по теории групп.-Киев: Наукова думка, 1980-с.189-195
3. Монахов В.С. О произведении двух групп с циклическими подгруппами индекса 2// Весцi АН Беларусi. сер. фiз.-мат. навук.-1996, №3-с.21-24
Похожие работы
... нужно самому вести рассказ вслед за ребенком, повторяя то, что он сказал, и обязательно, добавляя пропущенное. 3. Методика ознакомления с литературными произведениями детей младшего дошкольного возраста (до 3 лет) Если в задачах работы по развитию звуковой культуры речи в 1 младшей группе на первое место ставилось звукоподражание, то во 2 - эта работа над звукопроизношением с развитием ...
... результат работы(6), мы доказываем в настоящей заметке следующую теорему. Теорема Пусть конечная группа является произведением своих подгрупп и взаимно простых порядков, и пусть --- бипримарная группа, а --- 2-разложимая группа четного порядка. Предположим, что в есть неединичная циклическая силовская подгруппа . Тогда, если неразрешима, то изоморфна или . обозначает произведение ...
... , т.е. . Здесь обозначает матрицу, транспонированную к , где , а – величина, комплексно – сопряженная к . В этом параграфе мы покажем, что каждое представление конечной группы эквивалентно некоторому ее унитарному представлению и является мполне приводимым. Матрица называется эрмитовой, если , и положительно определенной, если для каждого ненулевого столбца . Следующая лемма тривиальна. ...
... тогда и только тогда, когда она разложима в произведение попарно перестановочных -подгрупп по разным простым 1.2.35 Т е о р е м а (Кегель [31] – Виландт [4]). Конечная группа, представимая в виде произведения некоторых своих попарно перестановочных нильпотентных подгрупп, разрешима. 1.2.36 Т е о р е м а. Пусть – некоторое множество простых чисел; – группа, факторизуемая подгруппами и где ...
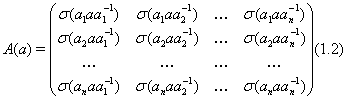
0 комментариев