Навигация
О произведении двух групп с циклическими подгруппами индекса 2
В 1953 г. Б. Хупперт установил разрешимость конечной группы, которая является произведением двух диэдральных подгрупп. Развивая этот результат, В. Скотт получил разрешимость конечной группы ![]() , допустив в качестве множителей еще так называемые дициклические группы. Эти результаты достаточно подробно изложены в монографии. Диэдральные и дицикдические группы содержат циклические подгруппы индекса 2, но далеко не исчерпывают весь класс групп с циклическими подгруппами индекса 2.
, допустив в качестве множителей еще так называемые дициклические группы. Эти результаты достаточно подробно изложены в монографии. Диэдральные и дицикдические группы содержат циклические подгруппы индекса 2, но далеко не исчерпывают весь класс групп с циклическими подгруппами индекса 2.
В 1974 г. автор установил разрешимость конечной группы ![]() при условии, что факторы
при условии, что факторы ![]() и
и ![]() содержат циклические подгруппы индексов 2, тем самым решив задачу, рассматриваемую Хуппертом и Скоттом. В настоящей заметке показывается, что 2-длина таких групп не превышает 2, а
содержат циклические подгруппы индексов 2, тем самым решив задачу, рассматриваемую Хуппертом и Скоттом. В настоящей заметке показывается, что 2-длина таких групп не превышает 2, а ![]() -длина равна 1 для любого нечетного
-длина равна 1 для любого нечетного ![]() . Эти оценки точные, на что указывает пример симметрической группы
. Эти оценки точные, на что указывает пример симметрической группы ![]() . Получены также два признака сверхразрешимости конечной факторизуемой группы.
. Получены также два признака сверхразрешимости конечной факторизуемой группы.
Все встречающиеся определения и обозначения общеприняты. В частности, ![]() - множество простых делителей порядка
- множество простых делителей порядка ![]() , a
, a ![]() - циклическая группа порядка
- циклическая группа порядка ![]() .
.
Лемма 1 . Метациклическая группа порядка ![]() для нечетного простого
для нечетного простого ![]() неразложима в полупрямое произведение нормальной элементарной абелевой подгруппы порядка
неразложима в полупрямое произведение нормальной элементарной абелевой подгруппы порядка ![]() и подгруппы порядка
и подгруппы порядка ![]() .
.
Доказательство. Допустим противное и пусть ![]() - метациклическая группа порядка
- метациклическая группа порядка ![]() , разложимая в полупрямое произведение нормальной элементарной абелевой подгруппы
, разложимая в полупрямое произведение нормальной элементарной абелевой подгруппы ![]() порядка
порядка ![]() и подгруппы
и подгруппы ![]() порядка
порядка ![]() ,
, ![]() - нечетное простое число. Ясно, что
- нечетное простое число. Ясно, что ![]() неабелева. Если
неабелева. Если ![]() содержит нормальную подгруппу
содержит нормальную подгруппу ![]() порядка
порядка ![]() с циклической фактор-группой
с циклической фактор-группой ![]() , то
, то ![]() содержится в центре
содержится в центре ![]() и
и ![]() абелева по лемме 1.3.4, противоречие. Следовательно,
абелева по лемме 1.3.4, противоречие. Следовательно, ![]() содержит циклическую подгруппу индекса
содержит циклическую подгруппу индекса ![]() и подгруппа
и подгруппа ![]() , порожденная элементами порядка
, порожденная элементами порядка ![]() , является элементарной абелевой подгруппой порядка
, является элементарной абелевой подгруппой порядка ![]() по теоремам 5.4.3 и 5.4.4. Теперь
по теоремам 5.4.3 и 5.4.4. Теперь ![]() , и подгруппы
, и подгруппы ![]() порядка
порядка ![]() не существует. Значит, допущение неверно и лемма справедлива.
не существует. Значит, допущение неверно и лемма справедлива.
При ![]() утверждение леммы неверно, контрпримером служит диэдральная группа порядка 8.
утверждение леммы неверно, контрпримером служит диэдральная группа порядка 8.
Лемма 2 . Разрешимая конечная группа с циклической подгруппой Фиттинга сверхразрешима.
Доказательство. Пусть ![]() - конечная разрешимая группа с циклической подгруппой Фиттинга
- конечная разрешимая группа с циклической подгруппой Фиттинга ![]() . Так как
. Так как ![]() , то
, то ![]() как группа автоморфизмов циклической группы будет абелевой по теореме 1.3.10, поэтому
как группа автоморфизмов циклической группы будет абелевой по теореме 1.3.10, поэтому ![]() сверхразрешима.
сверхразрешима.
Лемма 3 . Если в сверхразрешимой группе нет неединичных нормальных 2-подгрупп, то силовская 2-подгруппа абелева.
Доказательство. Коммутант сверхразрешимой группы нильпотентен (теорема VI.9.1), поэтому силовская 2-подгруппа из коммутанта нормальна в группе. Если коммутант имеет нечетный порядок, то силовская 2-подгруппа в группе абелева.
Напомним, что ![]() - наибольшая нормальная в
- наибольшая нормальная в ![]()
![]() -подгруппа,
-подгруппа, ![]() - центр группы
- центр группы ![]() , а
, а ![]() - наименьшая нормальная в
- наименьшая нормальная в ![]() подгруппа, содержащая
подгруппа, содержащая ![]() . Через
. Через ![]() обозначается
обозначается ![]() -длина группы
-длина группы ![]() .
.
Лемма 4 . Пусть ![]() и
и ![]() - подгруппы конечной группы
- подгруппы конечной группы ![]() , обладающие, следующими свойствами:
, обладающие, следующими свойствами:
1) ![]() для всех
для всех ![]() ;
;
2) ![]() , где
, где ![]() .
.
Тогда ![]() .
.
Доказательство. См. лемму 1.
Теорема 1 . Пусть конечная группа ![]() , где
, где ![]() и
и ![]() - группы с циклическими подгруппами индексов
- группы с циклическими подгруппами индексов ![]() . Тогда
. Тогда ![]() разрешима,
разрешима, ![]() и
и ![]() для любого простого нечетного
для любого простого нечетного ![]() .
.
Доказательство. По теореме из группа ![]() разрешима. Для вычисления
разрешима. Для вычисления ![]() -длины воспользуемся индукцией по порядку группы
-длины воспользуемся индукцией по порядку группы ![]() . Вначале рассмотрим случай нечетного
. Вначале рассмотрим случай нечетного ![]() . По лемме VI.6.4 подгруппа Фраттини единична и в группе
. По лемме VI.6.4 подгруппа Фраттини единична и в группе ![]() единственная минимальная нормальная подгруппа. По теореме III.4.5 подгруппа Фиттинга
единственная минимальная нормальная подгруппа. По теореме III.4.5 подгруппа Фиттинга ![]() - минимальная нормальная подгруппа. Так как
- минимальная нормальная подгруппа. Так как ![]() , то
, то ![]() -
- ![]() -группа. Если
-группа. Если ![]() , то
, то ![]() - абелева группа порядка, делящего
- абелева группа порядка, делящего ![]() , а так как
, а так как ![]() , то
, то ![]() . Силовская
. Силовская ![]() -подгруппа в
-подгруппа в ![]() метациклическая по теореме III.11.5, поэтому
метациклическая по теореме III.11.5, поэтому ![]() - элементарная абелева порядка
- элементарная абелева порядка ![]() и
и ![]() изоморфна подгруппе из
изоморфна подгруппе из ![]() , в которой силовская
, в которой силовская ![]() -подгруппа имеет порядок
-подгруппа имеет порядок ![]() . Так как
. Так как ![]() для некоторой максимальной в
для некоторой максимальной в ![]() подгруппы
подгруппы ![]() , то из леммы 1 получаем что
, то из леммы 1 получаем что ![]() - силовская в
- силовская в ![]() подгруппа и
подгруппа и ![]() .
.
Рассмотрим теперь 2-длину группы ![]() . Ясно, что
. Ясно, что ![]() и
и ![]() - единственная минимальная нормальная в
- единственная минимальная нормальная в ![]() подгруппа, которая является элементарной абелевой 2-подгруппой. Пусть
подгруппа, которая является элементарной абелевой 2-подгруппой. Пусть ![]() и
и ![]() -
- ![]() -холловские подгруппы из
-холловские подгруппы из ![]() и
и ![]() соответственно. По условию теоремы
соответственно. По условию теоремы ![]() - циклическая нормальная в
- циклическая нормальная в ![]() подгруппа,
подгруппа, ![]() - циклическая нормальная в
- циклическая нормальная в ![]() подгруппа. Теперь
подгруппа. Теперь ![]() -
- ![]() -холловская в
-холловская в ![]() подгруппа по теореме VI.4.6, и можно считать, что
подгруппа по теореме VI.4.6, и можно считать, что ![]() . Для любого элемента
. Для любого элемента ![]() имеем:
имеем: ![]() , a по лемме 4 либо
, a по лемме 4 либо ![]() , либо
, либо ![]() . Но если
. Но если ![]() , то
, то ![]() и
и ![]() централизует
централизует ![]() , что невозможно. Значит,
, что невозможно. Значит, ![]() , а так как в
, а так как в ![]() только одна минимальная нормальная подгруппа, то
только одна минимальная нормальная подгруппа, то ![]() и
и ![]() - 2-группа. Фактор-группа
- 2-группа. Фактор-группа ![]() не содержит нормальных неединичных 2-подгрупп, поэтому подгруппа Фиттинга
не содержит нормальных неединичных 2-подгрупп, поэтому подгруппа Фиттинга ![]() имеет нечетный порядок. Но
имеет нечетный порядок. Но ![]() -холловская в
-холловская в ![]() подгруппа
подгруппа ![]() циклическая, а по лемме 2 фактор-группа
циклическая, а по лемме 2 фактор-группа ![]() сверхразрешима и силовская 2-подгруппа в
сверхразрешима и силовская 2-подгруппа в ![]() абелева по лемме 3, Теперь
абелева по лемме 3, Теперь ![]() по теореме VI.6.6 и
по теореме VI.6.6 и ![]() . Теорема доказана.
. Теорема доказана.
Лемма 5 . Конечная группа с подгруппой Фиттинга индекса ![]() сверхразрешима.
сверхразрешима.
Доказательство. Проведем индукцией по порядку группы. Пусть ![]() - конечная группа, в которой подгруппа Фиттинга
- конечная группа, в которой подгруппа Фиттинга ![]() имеет индекс
имеет индекс ![]() . По индукции можно считать, что подгруппа Фраттини единична и в группе
. По индукции можно считать, что подгруппа Фраттини единична и в группе ![]() только одна минимальная нормальная подгруппа. Поэтому F - минимальная нормальная в
только одна минимальная нормальная подгруппа. Поэтому F - минимальная нормальная в ![]() подгруппа. Пусть
подгруппа. Пусть ![]() - инволюция из
- инволюция из ![]() . Если
. Если ![]() , то
, то ![]() - нормальная в
- нормальная в ![]() подгруппа. Если
подгруппа. Если ![]() , то
, то ![]() и
и ![]() - неединичная нормальная в
- неединичная нормальная в ![]() подгруппа. Итак, в группе
подгруппа. Итак, в группе ![]() имеется нормальная подгруппа
имеется нормальная подгруппа ![]() простого порядка. По индукции
простого порядка. По индукции ![]() сверхразрешима, значит, сверхразрешима и группа
сверхразрешима, значит, сверхразрешима и группа ![]() .
.
Лемма 6 . Конечная группа, являющаяся произведением двух подгрупп порядков, делящих ![]() , сверхразрешима.
, сверхразрешима.
Доказательство. Воспользуемся индукцией по порядку группы. Пусть конечная группа ![]() , где подгруппы
, где подгруппы ![]() и
и ![]() имеют порядки, делящие
имеют порядки, делящие ![]() ,
, ![]() - простое число. Все фактор-группы группы
- простое число. Все фактор-группы группы ![]() удовлетворяют условиям леммы, поэтому по индукции нетривиальные фактор-группы группы
удовлетворяют условиям леммы, поэтому по индукции нетривиальные фактор-группы группы ![]() сверхразрешимы. Следовательно, подгруппа Фраттини группы
сверхразрешимы. Следовательно, подгруппа Фраттини группы ![]() единична, а подгруппа Фиттинга
единична, а подгруппа Фиттинга ![]() - минимальная нормальная в
- минимальная нормальная в ![]() подгруппа. По лемме 2 подгруппа
подгруппа. По лемме 2 подгруппа ![]() нециклическая.
нециклическая.
Если ![]() - 2-группа, то
- 2-группа, то ![]() и
и ![]() изоморфна подгруппе группы
изоморфна подгруппе группы ![]() , поэтому
, поэтому ![]() - группа порядка 3, а группа
- группа порядка 3, а группа ![]() имеет порядок 12 и содержит подгруппу порядка 6. Следовательно,
имеет порядок 12 и содержит подгруппу порядка 6. Следовательно, ![]() сверхразрешима.
сверхразрешима.
Пусть теперь ![]() -
- ![]() -группа. Так как
-группа. Так как ![]() сверхразрешима по индукции, то
сверхразрешима по индукции, то ![]() 2-нильпотентна. Но
2-нильпотентна. Но ![]() , так как
, так как ![]() , значит,
, значит, ![]() - 2-группа, которая по лемме 5 имеет порядок 4. Группа
- 2-группа, которая по лемме 5 имеет порядок 4. Группа ![]() неприводимо действует на подгруппе
неприводимо действует на подгруппе ![]() , поэтому
, поэтому ![]() циклическая по теореме Машке. С другой стороны,
циклическая по теореме Машке. С другой стороны, ![]() и силовская 2-подгруппа
и силовская 2-подгруппа ![]() из
из ![]() есть произведение двух подгрупп
есть произведение двух подгрупп ![]() и
и ![]() порядков 2. Противоречие. Лемма доказана.
порядков 2. Противоречие. Лемма доказана.
Теорема 2. Если группы ![]() и
и ![]() содержат циклические подгруппы нечетных порядков и индексов
содержат циклические подгруппы нечетных порядков и индексов ![]() , то конечная группа
, то конечная группа ![]() сверхразрешима.
сверхразрешима.
Доказательство. Воспользуемся индукцией по порядку группы. По теореме 1 группа ![]() разрешима. Поскольку условия теоремы переносятся на все фактор-группы, то по индукции все нетривиальные фактор-группы группы
разрешима. Поскольку условия теоремы переносятся на все фактор-группы, то по индукции все нетривиальные фактор-группы группы ![]() сверхразрешимы. Поэтому подгруппа Фраттини группы
сверхразрешимы. Поэтому подгруппа Фраттини группы ![]() единична, а подгруппа Фиттинга
единична, а подгруппа Фиттинга ![]() - единственная минимальная нормальная в
- единственная минимальная нормальная в ![]() подгруппа. Ясно, что
подгруппа. Ясно, что ![]() имеет непростой порядок. Если
имеет непростой порядок. Если ![]() - 2-группа, то
- 2-группа, то ![]() порядка 4 и
порядка 4 и ![]() изоморфна подгруппе группы
изоморфна подгруппе группы ![]() . Но теперь порядок
. Но теперь порядок ![]() делит 12, и
делит 12, и ![]() сверхразрешима по лемме 6.
сверхразрешима по лемме 6.
Следовательно, ![]() -
- ![]() -группа порядка
-группа порядка ![]() . Силовская
. Силовская ![]() -подгруппа в
-подгруппа в ![]() метациклическая по теореме III.11.5, поэтому
метациклическая по теореме III.11.5, поэтому ![]() - элементарная абелева порядка
- элементарная абелева порядка ![]() и
и ![]() изоморфна подгруппе группы
изоморфна подгруппе группы ![]() , в которой силовская
, в которой силовская ![]() -подгруппа имеет порядок
-подгруппа имеет порядок ![]() . Так как
. Так как ![]() для некоторой максимальной в
для некоторой максимальной в ![]() подгруппы
подгруппы ![]() , то из леммы 1 получаем, что
, то из леммы 1 получаем, что ![]() - силовская в
- силовская в ![]() подгруппа и можно считать, что
подгруппа и можно считать, что ![]() , где
, где ![]() .
.
Через ![]() - обозначим разность
- обозначим разность ![]() . Так как
. Так как ![]() -холловские подгруппы
-холловские подгруппы ![]() из
из ![]() и
и ![]() из
из ![]() нормальны в
нормальны в ![]() и
и ![]() соответственно, то
соответственно, то ![]() -
- ![]() -холловская в
-холловская в ![]() подгруппа. Если
подгруппа. Если ![]() , то
, то ![]() сверхразрешима по лемме 6. Пусть
сверхразрешима по лемме 6. Пусть ![]() . Для любого элемента
. Для любого элемента ![]() имеем:
имеем: ![]() и по лемме 4 либо
и по лемме 4 либо ![]() , либо
, либо ![]() . Если
. Если ![]() , то из минимальности
, то из минимальности ![]() получаем, что
получаем, что ![]() и
и ![]() централизует
централизует ![]() , что невозможно. Значит,
, что невозможно. Значит, ![]() и
и ![]() . Но в
. Но в ![]() единственная минимальная нормальная подгруппа, поэтому
единственная минимальная нормальная подгруппа, поэтому ![]() и
и ![]() делит
делит ![]() . Но если
. Но если ![]() , то
, то ![]() нормальна в
нормальна в ![]() , противоречие. Значит,
, противоречие. Значит, ![]() .
.
Так как ![]() сверхразрешима и
сверхразрешима и ![]() -
- ![]() -холловская подгруппа в
-холловская подгруппа в ![]() , то
, то ![]() нормальна в
нормальна в ![]() и по лемме Фраттини
и по лемме Фраттини ![]() содержит силовскую 2-подгруппу
содержит силовскую 2-подгруппу ![]() из
из ![]() . Ясно, что
. Ясно, что ![]() . Подгруппа
. Подгруппа ![]() ненормальна в
ненормальна в ![]() , значит,
, значит, ![]() , но теперь
, но теперь ![]() нормальна в
нормальна в ![]() и нормальна в
и нормальна в ![]() , противоречие. Теорема доказана.
, противоречие. Теорема доказана.
Теорема 3 . Пусть конечная группа ![]() , где
, где ![]() - циклическая подгруппа нечетного порядка, а подгруппа
- циклическая подгруппа нечетного порядка, а подгруппа ![]() содержит циклическую подгруппу индекса
содержит циклическую подгруппу индекса ![]() . Если в
. Если в ![]() нет нормальных секций, изоморфных
нет нормальных секций, изоморфных ![]() , то
, то ![]() сверхразрешима.
сверхразрешима.
Доказательство. Воспользуемся индукцией по порядку группы. По теореме 1 группа ![]() разрешима, а так как условия теоремы переносятся на все фактор-группы, то подгруппа Фиттинга
разрешима, а так как условия теоремы переносятся на все фактор-группы, то подгруппа Фиттинга ![]() - единственная минимальная нормальная в
- единственная минимальная нормальная в ![]() подгруппа. Если
подгруппа. Если ![]() - 2-группа, то
- 2-группа, то ![]() содержится в
содержится в ![]() и поэтому порядок
и поэтому порядок ![]() равен 4, a
равен 4, a ![]() изоморфна подгруппе группы
изоморфна подгруппе группы ![]() . Если силовская 3-подгруппа
. Если силовская 3-подгруппа ![]() из
из ![]() неединична, то
неединична, то ![]() действует на
действует на ![]() неприводимо и
неприводимо и ![]() - нормальная в
- нормальная в ![]() подгруппа, изоморфная
подгруппа, изоморфная ![]() , противоречие. Если
, противоречие. Если ![]() , то
, то ![]() - 2-группа и
- 2-группа и ![]() сверхразрешима.
сверхразрешима.
Следовательно, ![]() -
- ![]() -группа порядка
-группа порядка ![]() . Так как силовская
. Так как силовская ![]() -подгруппа в
-подгруппа в ![]() метациклическая по теореме III.11.5, то
метациклическая по теореме III.11.5, то ![]() - элементарная абелева порядка
- элементарная абелева порядка ![]() и
и ![]() изоморфна подгруппе из
изоморфна подгруппе из ![]() , в которой силовская
, в которой силовская ![]() -подгруппа имеет порядок
-подгруппа имеет порядок ![]() . Так как
. Так как ![]() для некоторой максимальной в
для некоторой максимальной в ![]() подгруппы
подгруппы ![]() , то из леммы 1 получаем, что
, то из леммы 1 получаем, что ![]() - силовская в
- силовская в ![]() подгруппа и можно считать, что
подгруппа и можно считать, что ![]() , где
, где ![]() , a
, a ![]() .
.
Через ![]() обозначим
обозначим ![]() . Как и в теореме 2, легко показать, что
. Как и в теореме 2, легко показать, что ![]() -холловская подгруппа
-холловская подгруппа ![]() из
из ![]() неединична, а
неединична, а ![]() . Так как
. Так как ![]() -
- ![]() -холловская в
-холловская в ![]() подгруппа и
подгруппа и ![]() сверхразрешима, то
сверхразрешима, то ![]() нормальна в
нормальна в ![]() и
и ![]() содержит силовскую 2-подгруппу
содержит силовскую 2-подгруппу ![]() из
из ![]() , которая совпадает с силовской 2-подгруппой в
, которая совпадает с силовской 2-подгруппой в ![]() . Подгруппа
. Подгруппа ![]() ненормальна в
ненормальна в ![]() , поэтому
, поэтому ![]() . Но теперь
. Но теперь ![]() нормальна в
нормальна в ![]() , а значит, и в
, а значит, и в ![]() , противоречие. Теорема доказана.
, противоречие. Теорема доказана.
Похожие работы
... нужно самому вести рассказ вслед за ребенком, повторяя то, что он сказал, и обязательно, добавляя пропущенное. 3. Методика ознакомления с литературными произведениями детей младшего дошкольного возраста (до 3 лет) Если в задачах работы по развитию звуковой культуры речи в 1 младшей группе на первое место ставилось звукоподражание, то во 2 - эта работа над звукопроизношением с развитием ...
... результат работы(6), мы доказываем в настоящей заметке следующую теорему. Теорема Пусть конечная группа является произведением своих подгрупп и взаимно простых порядков, и пусть --- бипримарная группа, а --- 2-разложимая группа четного порядка. Предположим, что в есть неединичная циклическая силовская подгруппа . Тогда, если неразрешима, то изоморфна или . обозначает произведение ...
... , т.е. . Здесь обозначает матрицу, транспонированную к , где , а – величина, комплексно – сопряженная к . В этом параграфе мы покажем, что каждое представление конечной группы эквивалентно некоторому ее унитарному представлению и является мполне приводимым. Матрица называется эрмитовой, если , и положительно определенной, если для каждого ненулевого столбца . Следующая лемма тривиальна. ...
... тогда и только тогда, когда она разложима в произведение попарно перестановочных -подгрупп по разным простым 1.2.35 Т е о р е м а (Кегель [31] – Виландт [4]). Конечная группа, представимая в виде произведения некоторых своих попарно перестановочных нильпотентных подгрупп, разрешима. 1.2.36 Т е о р е м а. Пусть – некоторое множество простых чисел; – группа, факторизуемая подгруппами и где ...
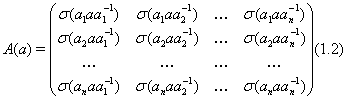

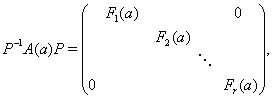

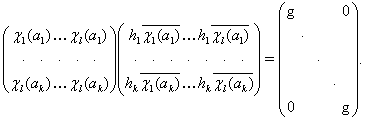
0 комментариев