Навигация
СИЛОВОЕ ИССЛЕДОВАНИЕ МЕХАНИЗМОВ
3. СИЛОВОЕ ИССЛЕДОВАНИЕ МЕХАНИЗМОВ
В задачу силового исследования входит определение:
1) сил, действующих на звенья механизма;
2) реакций в кинематических парах;
3) уравновешивающей силы (момента).
Силовой анализ основан на принципе Даламбера. Сущность его заключается в том, что каждое звено может рассматриваться в условном статическом равновесии, если к нему помимо всех действующих внешних сил приложить инерционную нагрузку в виде силы инерции и момента пары сил инерции. При этом условии для каждого звена справедливы равенства:
![]()
![]() , (3.1)
, (3.1)
поэтому неизвестные силы (реакции в кинематических парах) могут определяться методом статики.
Для проведения силового анализа кинематическая цепь должна быть статически определимой, т. е. число неизвестных параметров реакций должно быть равно количеству уравнений статики, которые можно составить для их определения.
Начинать силовой анализ необходимо с наиболее удаленной от ведущего звена структурной группы.
3.1 Определение реакций в кинематических парах структурных групп
Чтобы определить величины и направления сил инерции, надо знать ускорения и массы звеньев. Ускорения известны из плана ускорений механизма. Определяем вес каждого звена, Н:
![]() ;
;
![]() ;
;
![]() ; (3.2)
; (3.2)
![]() ;
;
![]() ;
;
где ![]() - длина звеньев, мм.
- длина звеньев, мм.
Определяем массу каждого звена, кг:
 ;
; 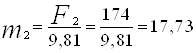 ;
;
 ;
; 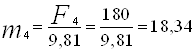 ; (3,3)
; (3,3)
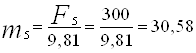 .
.
Определяем силы инерции звеньев, Н:
![]() ;
;
![]() ;
;
![]() ; (3.4)
; (3.4)
![]() ;
;
![]() .
.
Определяем момент пары сил инерции для звеньев CD, О2B и AВ, совершающих сложное движение:
звено АВ- ![]()
![]() (3.5)
(3.5)
![]()
звено О2B-
![]() ;
;
![]() ; (3.6)
; (3.6)
![]()
звено СD- ![]()
![]() (3.5)
(3.5)
![]()
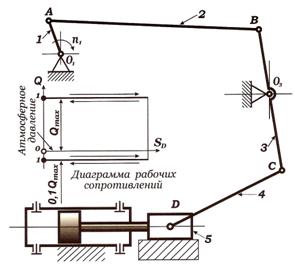
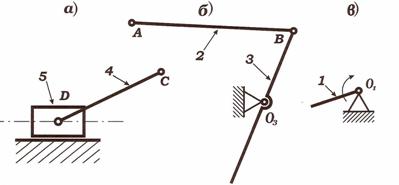
Силовой расчет механизма начинаем с наиболее удаленной от ведущего звена группы Ассура 4 – 5 (CD), состоящей из звеньев 4 и 5, двух вращательных кинематических пар – С и D, и одной поступательной (при движении ползуна по направляющей).
Группу CD вычерчиваем отдельно в масштабе схемы механизма и в том же положении. Прикладываем к ней вместо связей две реакции:
F65 – в поступательной паре, другую F34 в шарнире С, неизменные по величине и направлению. Реакцию F34 представляем в виде двух составляющих: тангенциальной ![]() , направленной перпендикулярно к оси звена CD, и нормальной
, направленной перпендикулярно к оси звена CD, и нормальной ![]() - вдоль звена CD.
- вдоль звена CD.
Кроме этого прикладываем силы веса F4 и F5 в центрах тяжести и силы инерции: ![]() - против ускорения тяжести S4 ;
- против ускорения тяжести S4 ; ![]() - против ускорения ползуна
- против ускорения ползуна ![]() . Момент инерции
. Момент инерции ![]() заменяем парой сил:
заменяем парой сил: ![]() , приложенной в точке С против направления углового ускорения звена 4 (e4), и
, приложенной в точке С против направления углового ускорения звена 4 (e4), и ![]() - в точке D.
- в точке D.
Для определения реакций в кинематических парах составляем векторное уравнение равновесия сил, действующих на группу 4 – 5 по порядку звеньев:
![]() . (3.7)
. (3.7)
Силы ![]() и
и ![]() в уравнение не вписаны, так как они решается построением плана сил, и эти силы взаимно уравновешивают друг друга, но для определения
в уравнение не вписаны, так как они решается построением плана сил, и эти силы взаимно уравновешивают друг друга, но для определения ![]() эти силы надо знать, Н:
эти силы надо знать, Н:
 ;
; ![]()
 ; (3.8)
; (3.8)
Определяем ![]() , входящую в уравнение равновесия, составив уравнение моментов всех сил, действующих на звено CD, относительно точки D:
, входящую в уравнение равновесия, составив уравнение моментов всех сил, действующих на звено CD, относительно точки D:
![]() ; (3.9)
; (3.9)
![]()
![]() Н.
Н.
Поскольку составляющую ![]() получилась со знаком плюс, то это значит, что ее действительное направление совпадает с выбранным.
получилась со знаком плюс, то это значит, что ее действительное направление совпадает с выбранным.
Исходя из значений сил, входящих в уравнение равновесия, Н:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() ; (3.10)
; (3.10)
задаемся масштабом плана сил ![]() , Н/мм.
, Н/мм.
Максимальной силой является сила полезного сопротивления, которую в примере изобразим вектором длиной 250 мм. Получаем масштаб плана сил, Н × мм-1:
![]() . (3.11)
. (3.11)
Вычисляем длины векторов, мм, изображающих эти силы, поделив их численные значения на масштаб:
![]()
![]() ;
; ![]()
![]() ;
;
![]()
![]() ;
; ![]()
![]() (3.12)
(3.12)
![]() (задались);
(задались); ![]()
![]()
От произвольной точки – полюса плана сил – параллельно силе ![]() откладываем вектор
откладываем вектор ![]() изображающий эту силу; от конца вектора
изображающий эту силу; от конца вектора ![]() параллельно силе
параллельно силе ![]() откладываем в том же направлении вектор
откладываем в том же направлении вектор ![]() и далее векторы всех сил. Через точку а параллельно звену СD проводим линию действия
и далее векторы всех сил. Через точку а параллельно звену СD проводим линию действия ![]() , а через конец вектора
, а через конец вектора ![]() перпендикулярно к направляющей ползуна – линию действия силы
перпендикулярно к направляющей ползуна – линию действия силы ![]() . Точка пересечения этих линий действия определяет силы
. Точка пересечения этих линий действия определяет силы ![]() ,
, ![]() ,
, ![]() Н:
Н:
![]()
![]() ; (3.13)
; (3.13)
![]()
![]() ;
;
![]()
![]()
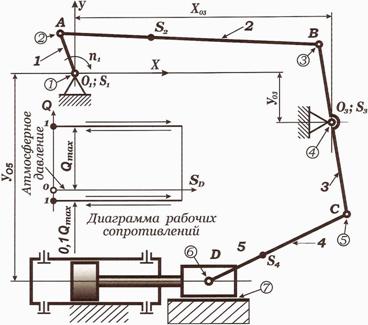
Далее следует отсоединить группу Ассура АВСО2, состоящую из звеньев 2 и 3, вычертить ее в масштабе. В соответствующих точках приложить действующие силы: ![]() . Реакцию в шарнире А и О2 представить в виде двух составляющих –
. Реакцию в шарнире А и О2 представить в виде двух составляющих – ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Реакцию со стороны звена 4 на звено 3
. Реакцию со стороны звена 4 на звено 3 ![]() , полученную из плана сил группы Ассура CD,
, полученную из плана сил группы Ассура CD, ![]() приложить в обратном направлении в точке С звена 2
приложить в обратном направлении в точке С звена 2 ![]() .
.
Составляем векторное уравнение равновесия сил, действующих на группу Ассура 2 – 3 , по порядку звеньев:
![]() . (3.17)
. (3.17)
Силы ![]() ,
,![]() ,
,![]() и
и ![]() в уравнение не вписываем, так как это уравнение решается построением плана сил, и они взаимно уравновешивают друг друга. Но для определения
в уравнение не вписываем, так как это уравнение решается построением плана сил, и они взаимно уравновешивают друг друга. Но для определения ![]() и
и ![]() эти силы надо знать, определяем их, Н:
эти силы надо знать, определяем их, Н:

![]() (3.1)
(3.1)
 ;
; ![]()
![]()
Из уравнения моментов относительно точки В для звена 2 определяем составляющую ![]() , Н:
, Н:
![]() (3.19)
(3.19)
отсюда,
![]() ; (3.20)
; (3.20)
![]()
Размеры плеч ![]() снимаем с чертежа в миллиметрах. Поскольку знак составляющей
снимаем с чертежа в миллиметрах. Поскольку знак составляющей ![]() изменился, то ее действительное направление не соответствует выбранному.
изменился, то ее действительное направление не соответствует выбранному.
Определяем тангенциальную составляющую ![]() из уравнения моментов относительно точки В для звена 3:
из уравнения моментов относительно точки В для звена 3:
![]() ;
;
![]() (3.21)
(3.21)
![]()
Плечи ![]() ,
, ![]() ,
, ![]() снимаем с чертежа в миллиметрах. Поскольку составляющая
снимаем с чертежа в миллиметрах. Поскольку составляющая ![]() получилась со знаком минус, то это значит, что её действительное направление не совпадает с выбранным.
получилась со знаком минус, то это значит, что её действительное направление не совпадает с выбранным.
Выписав значения всех сил, Н, действующих на группу Ассура, по максимальной из них задаемся масштабом. Максимальную силу F43 изобразим вектором, длина которого 308 мм (произвольно), тогда:
![]() Н/мм. (3.22)
Н/мм. (3.22)
Вычисляем длины векторов, изображающих эти силы, мм:
![]()
![]() ;
; ![]()
![]() ;
;
![]()
![]() ;
; ![]()
![]() (3.23)
(3.23)
![]()
![]() ;
; 
![]() ;
;
![]()
![]()
Строим план сил, из которого определяем нормальные составляющие ![]() и результирующие величины давлений в шарнирах В и О2:
и результирующие величины давлений в шарнирах В и О2:
![]()
![]() (3.24)
(3.24)
![]()
![]()
![]()
Расчет ведущего звена производим с учетом действующих на него сил: ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() Сила
Сила ![]() известна по значению и направлению, а силы
известна по значению и направлению, а силы ![]() и
и ![]() неизвестны.
неизвестны.
Для определения значения ![]() составляем уравнение моментов всех сил, действующих на звено 1, относительно точки О1:
составляем уравнение моментов всех сил, действующих на звено 1, относительно точки О1:
![]() ; (3.25)
; (3.25)

![]() Н.
Н.
Определяем реакцию ![]() по значению и направлению путем построения плана сил согласно векторному уравнению Н :
по значению и направлению путем построения плана сил согласно векторному уравнению Н :
![]() . (3.26)
. (3.26)
Выписав значения всех сил, Н, по максимальной из них задаемся
масштабом. Изобразим F21 = 2650.8Н вектором длиной 100 мм, тогда
![]() Н/мм. (3.27)
Н/мм. (3.27)
Вычисляем длины векторов всех сил для плана, мм:
![]()
![]() ;
; ![]() (задались)
(задались)
![]()
![]()
![]()
![]() (3.28)
(3.28)
Из плана сил определяем![]() :
:
![]()
![]() (3.29)
(3.29)
4.ГЕОМЕТРИЧЕСКИЙ СИНТЕЗ ПРЯМОЗУБОГО ВНЕШНЕГО ЗАЦЕПЛЕНИЯ
Задачей синтеза является определение размеров и качественных показателей (коэффициента перекрытия, относительного скольжения и удельного давления) зубчатого зацепления.
В данной работе выполнен синтез двух зацеплений: нулевое и неравносмещенное.
Проектируя зубчатые колеса необходимо учитывать кроме геометрических и динамических условий, технологический процесс их изготовления. Эвольвенты профилей зубчатых колес нарезают методами копирования и обкатки.
В данной работе предусматривается геометрический расчет – выбор основных геометрических параметров, определение размеров колес и проверка качественных показателей для нулевого и неравносмещенного зацепления.
Похожие работы
... А. Черкудиновым (1959 г.), отразили состояние теории современного учения о механизмах. Одновременно И. И. Артоболевский начинает исследования в области теории механизмов машин автоматического действия: гидравлических, пневматических и гидропневматических. Для современных машин характерны вибрационные явления и существенное изменение массы в процессе работы. Чтобы учесть эти факторы, в большинстве ...
... механизма для обеспечения эффективного перехода на различные способы транспортирования в зависимости от свойств материала и выполняемой технологической операции. Разработке методов кинематического анализа механизмов транспортирования ткани швейных машин и соответствующего этой задаче алгоритмического и программного обеспечения посвящены работы. [67],[71],[72]. В работе Ю.Ю.Щербаня и В.А.Горобца ...
... , если к нему приложить уравновешивающую силу и моменты. 2.8 Сравним полученные значения Рур, рассчитанные по методу плана сил и методом рычага Жуковского. Вывод: Проведя силовой анализ механизма, определили реакцию опор, нашли уравновешивающую силу, выяснили, что на данный механизм влияют силы инерции. РАЗДЕЛ III Проектирование эвольвентного зубчатого зацепления Задачами ...
... ,5 – 174,5 90 Δ, % 0,00 0,00 0,00 0,00 0,00 0,00 0,00 ПРИВЕДЁННЫЕ ФАКТОРЫ Положение 2 Расчёт ЭВМ Погрешность Δ, % – 156,6 – 156,6 0,00 IПР 0,22 0,22 0,00 2. Синтез и анализ кулачкового механизма 2.1 Построение диаграмм движения толкателя 1. Строится заданная диаграмма ускорений толкателя. Максимальная ордината ...
0 комментариев