Системи парна-непара

3. Системи парна-непара

Розглянемо систему

(8)

Будемо вважати, що всюди надалі ця система задовольняє умовам:

а) Функція  безупинно диференцюєма, і тому, задача Коші для системи (8) має єдине рішення;

б) Права частина системи (8) -періодична по .

Лема 8 Нехай система (8) задовольняє умовам а) і б). Тоді продовжині на відрізок  рішення  цієї системи буде -періодичним тоді й тільки тоді, коли

– є непарна частина рішення .

Доказ. Нехай  – -періодичне рішення системи (8). Тоді

Необхідність доведена.

Нехай  – рішення системи (8), для якого . Тоді

і тому

Таким чином, крапка  є нерухлива крапка відображення за період, а рішення  – -періодичне.

Доведена лема, питання про періодичність рішення

зводить до обчислення одного зі значень непарної частини . Іноді відносно  можна сказати більше, ніж про саме рішення . Це дозволяє в таких випадках робити різні висновки щодо існування періодичних рішень у систем виду (8). Диференцуємі функції

задовольняють деякій системі диференціальних рівнянь. Перш, ніж виписати цю систему, помітимо:

(9)

тому що

рішення системи (8). Заміняючи в тотожності (9)  на  й з огляду на, що похідна парної функції – функція непарна, а похідна непарної функції – функція парна, одержуємо тотожність

(10)

З тотожностей (9) і (10) знайдемо похідні:

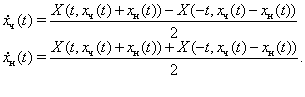
У такий спосіб вектор-функція

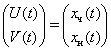(11)

задовольняє наступній системі диференціальних рівнянь порядку :

(12)

Систему (12) будемо називати системою пар-непара, що відповідає системі (8). рішення системи чіт-непара, як треба з умови а), однозначно визначається своїми початковими умовами.

4. Побудова прикладів систем, парна частина загального рішення яких постійна

Приклад

Знайдемо рішення: будемо використовувати метод виключення, візьмемо перше рівняння системи й виразимо з нього :

тепер диференціюємо його

Ми можемо дорівняти ліву частину отриманого рівняння з лівою частиною другого рівняння вихідної системи

Зробимо перетворення й приведемо подібні

У такий спосіб:

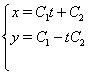
Зробимо перевірку, для цього у вихідну систему підставимо отримане рішення:

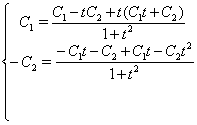
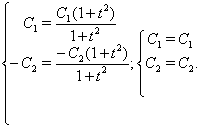
Одержали вірні рівності. Значить було знайдено правильне рішення вихідної системи.

Парна частина загального рішення:

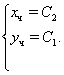
Приклад

Знайдемо рішення: будемо використовувати метод виключення, візьмемо перше рівняння системи й виразимо з нього :

тепер диференціюємо його

Ми можемо дорівняти ліву частину отриманого рівняння з лівою частиною другого рівняння вихідної системи

Зробимо перетворення й приведемо подібні

У такий спосіб:

Зробимо перевірку:

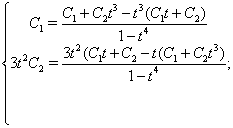
Парна частина загального рішення

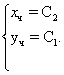
Приклад

Знайдемо рішення: будемо використовувати метод виключення, візьмемо перше рівняння системи й виразимо з нього :

тепер диференціюємо його

Ми можемо дорівняти ліву частину отриманого рівняння з лівою частиною другого рівняння вихідної системи

Одержали два рішення  й .

1) ;

2) ;

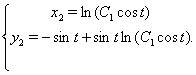
Зробимо перевірку для :

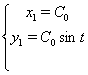
Одержали вірні рівності. Значить було знайдено правильне рішення вихідної системи.

Зробимо перевірку для :

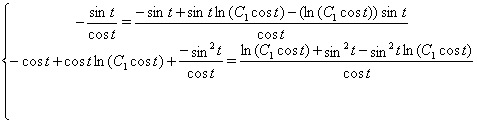
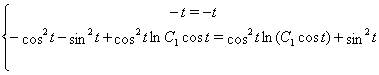
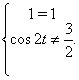
Звідси видно, що  не є рішенням для вихідної системи.

У такий спосіб:

Парна частина загального рішення

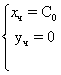
З даних прикладів можемо помітити, що рішення систем записується у вигляді:

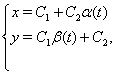
де  й  – непарні функції, а парна частина представлена константою.

;

;

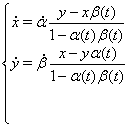(13)

Системи виду (13) будуть мати сімейства рішень із постійною парною частиною. У цьому легко переконається, проробивши обчислення, аналогічні попереднім прикладам.