Побудова множини систем, парна частина загального рішення яких постійна

6. Побудова множини систем, парна частина загального рішення яких постійна

6.1 Системи, що мають постійну парну частину

Нехай нам дана система

(14)

Перед нами встає наступне питання про те, коли сімейство рішень цієї системи будуть мати постійну парну частину.

(15)

Тобто, коли  не буде залежати від часу .

Візьмемо функцію, що відбиває, (14)  системи й використовуючи

одержимо парну частину в такий спосіб:

(16)

Теорема 15 Якщо виконано тотожність

де  – функція, що відбиває, для лінійної системи (14)виду , те будь-яке рішення цієї системи має постійну парну частину.

Доказ. Візьмемо будь-яке рішення  системи (14). Його похідна

Тому можемо записати

З умови теореми маємо

У такий спосіб одержали, що  – парна вектор-функція. Тоді

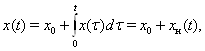
6.2 Побудова систем із заданою парною частиною

Розглянемо систему (14). Будемо будувати систему із заданою парною частиною.

Нехай нам відома парна частина . Скористаємося формулою (15) й перетворимо її

Отже, можемо записати

Звідси знаючи (3), одержимо

де  – функція, що відбиває, системи. Крім  із попереднього співвідношення, з довільною функцією, що відбиває , задовольняючій умові

одержимо необхідну систему.

Приклад 16 Нехай

де  – задана парна частина, . Диференціюємо обидві частини рівності

Перетворимо праву частину

Перепишемо отримане у вигляді:

Виразимо :

(17)

Для всіх систем виду (17) повинне бути виконане умова

Візьмемо

Знайдемо , . ;

Підставимо значення ,  у систему (17):

Одержуємо необхідну систему:

Приклад 17 Нехай

де  – задана парна частина, . Диференціюємо обидві частини рівності

і перетворимо праву частину

Перепишемо отримане у вигляді:

Виразимо :

(18)

Для всіх таких систем повинне бути виконане умова .

Візьмемо . Знайдемо , . ,

Підставимо знайдені значення в систему (18) й зробивши перетворення аналогічні прикладу 16, одержуємо:

Розглянемо тепер загальний випадок, коли нам задана парна частина  загального рішення системи з функцією, що відбиває . У цьому випадку

Тому, якщо  нам задана, то зі співвідношення

при заданій  ми знайдемо загальне рішення  шуканої системи. Саму систему ми побудуємо крім  зі співвідношень

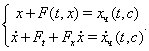
Таким чином, ми прийшли до

Теорема 18 Усяка система

(19)

де  перебувають із системи

при будь-якої заданої диференціюємої функції , що задовольняє співвідношенням

має загальне рішення з парною частиною .

Якщо

те система (19) має вигляд:

Таким чином, ми прийшли до висновку:

Наслідок 19 Загальне рішення диференціальної системи має постійну парну частину тоді й тільки тоді, коли ця система найпростіша.

Висновок

Основним результатом даної роботи є побудова диференціальних систем, сімейство рішень яких має задану парну частину. А так само теорема про зв'язок найпростішої системи й системи, сімейство рішень якої має постійну парну частину.

Теорема. Загальне рішення диференціальної системи має постійну парну частину тоді й тільки тоді, коли ця система найпростіша.

Список джерел

[1] Арнольд В.І., Звичайні диференціальні рівняння. – К., 2004

[2] Бібіков Ю.Н., Загальний курс диференціальних рівнянь. – К., 1999

[3] Еругин Н.П., Книга для читання за загальним курсом диференціальних рівнянь.3-е видання. – К., 2000

[4] Мироненко В.И., Функція й періодичні рішення диференціальних рівнянь. – К., 2004

[5] Понтрягин Л.С., Звичайні диференціальні рівняння. – К., 2003