Навигация
Установить наличие корреляционной связи между признаками Х и Y методом аналитической группировки
1. Установить наличие корреляционной связи между признаками Х и Y методом аналитической группировки.
Построив аналитическую таблицу, отражающую результаты аналитической группировки совокупности по факторному признаку Степень износа основных фондов в отрасли – строительство, можно установить наличие корреляционной связи.
Ранжируем исходные данные.
1.Выделить исходные данные табл. 2.1 (А4:С33);
2.Данные => Сортировка;
3.Сортировать по <= Степень износа основных фондов в отрасли – строительство
4.по возрастанию/по убыванию – устанавливается в положение по возрастанию;
5.Затем и В последнюю очередь по – не активизируются;
6.Идентифицировать поля по подписям/обозначениям столбцов листа – устанавливается в положение подписям
7.ОК.
В результате указанных действий в таблице 2.1 размещаются данные, ранжированные по возрастанию признака Среднегодовая стоимость основных производственных фондов.
Распределяем регионы по группам.
1.Из всего диапазона отсортированных данных A4:C33 выделить мышью диапазон ячеек первой группы, для чего необходимо отсчитать в ранжированном ряду количество строк, соответствующее числу предприятий первой группы (графа 3 табл.2.2),
2.Нажать на панели инструментов кнопку ![]() ;
;
3.Выбрать цвет по собственному усмотрению;
4.Выполнить действия 1–3 для всех групп, выбирая контрастные цвета для цветовой заливки очередной группы.
В итоге получаем таблицу 2.1. следующего вида:
Таблица 2.1. Исходные данные
| Регионы России | Степень износа основных фондов в отрасли – строительство, млн. руб. | Стоимость основных фондов в отрасли - строительство, млн. руб. |
| Республика Ингушетия | 68.54 | 149.00 |
| Курская область | 216.90 | 1446.00 |
| Калининградская область | 384.71 | 747.00 |
| Ивановская область | 386.60 | 1065.00 |
| Новгородская область | 674.08 | 1314.00 |
| Республика Карелия | 700.74 | 1530.00 |
| Калужская область | 733.04 | 1870.00 |
| Брянская область | 758.01 | 1919.00 |
| Липецкая область | 797.87 | 1797.00 |
| Тверская область | 814.43 | 1642.00 |
| Тамбовская область | 836.61 | 1855.00 |
| Мурманская область | 899.16 | 1905.00 |
| Псковская область | 907.41 | 2030.00 |
| Костромская область | 953.56 | 1516.00 |
| Тульская область | 989.33 | 2413.00 |
| Владимирская область | 1092.50 | 2595.00 |
| Вологодская область | 1098.59 | 3319.00 |
| Орловская область | 1109.12 | 1733.00 |
| Смоленская область | 1195.29 | 2330.00 |
| Республика Адыгея | 1361.26 | 2284.00 |
| Республика Дагестан | 1364.97 | 2630.00 |
| Воронежская область | 1479.63 | 3182.00 |
| Ленинградская область | 1971.00 | 4380.00 |
| Архангельская область | 2168.33 | 6285.00 |
| Ярославская область | 2411.03 | 5044.00 |
| Республика Коми | 2629.31 | 6351.00 |
А далее заполняем таблицу 2.2. формулами: в ячейку D44 вводим: =СУММ(C4:C7). Аналогично со следующими ячейками D45 - D48; в ячейку E44: =D44/C44.
Таблица 2.2. Зависимость стоимости основных фондов от степени износа основных фондов
| Номер группы | Группы областей по степени износа основных фондов в отрасли - строительство | Число областей | Стоимость основных фондов вотрасли - строительство | |
| Всего | В среднем на одну область | |||
| 1 | 68.54-580.69 | 4 | 3407.00 | 851.75 |
| 2 | 580.69-1092.85 | 12 | 22386.00 | 1865.50 |
| 3 | 1092.85-1605.0 | 6 | 15478.00 | 2579.67 |
| 4 | 1605.00-2117.16 | 1 | 4380.00 | 4380.00 |
| 5 | 2117.16-2629.31 | 3 | 17680.00 | 5893.33 |
| Итого | 26 | 63331.00 | 2435.81 | |
2. Оценить тесноту связи признаков Х и Y на основе:
а) эмпирического корреляционного отношения η;
б) линейного коэффициента корреляции r.
а)для вычисления эмпирического корреляционного отношения необходимо вычислить факторную и общую дисперсию, используя функции инструмента Мастер функций: ДИСПР, СУММПРОИЗВ, КОРЕНЬ.
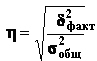
В ячейку А66 вводим формулу =ДИСПР(C4:C29); в ячейку В66: =СУММПРОИЗВ(D55:D59;C55:C59)/C49; в ячейку С66: =A66-B66. Теперь находим эмпирического корреляционного отношения η: в ячейку D66 вводим формулу: =КОРЕНЬ(C66/A66). В итоге получаем таблицу 2.4:
Показатели дисперсии и эмпирического корреляционного отношения
| Общая дисперсия | Средняя из внутригрупповых | Факторная дисперсия | Эмпирическое корреляционное отношение |
| 2266566.771 | 200894.76 | 2065672.01 | 0.954654939 |
Получаем η= 0.954654939.
б) для нахождения линейного коэффициента корреляции r используем инструмент Корреляция надстройки Пакет анализа.
1.Сервис => Анализ данных => Корреляция => ОК.
2.Входной интервал В4:С29;
3.Группирование – по столбцам;
4.Метки в первой строке – не активизировать;
5.Выходной интервал (А71);
6.Новый рабочий лист и Новая рабочая книга – не активизировать;
7.ОК.
В результате работы алгоритма Excel выдает оценку тесноты связи факторного и результативного признаков (табл. 2.5):
Таблица 2.5. Линейный коэффициент корреляции признаков
|
| Столбец 1 | Столбец 2 |
| Столбец 1 | 1 | |
| Столбец 2 | 0.946358973 | 1 |
Сравним значения η и r и сделаем вывод о возможности линейной связи между признаками Х и Y: так как они располагаются в диапазоне 0,9-0,99, то связь весьма тесная (по шкале Чэддока).
3. Построить однофакторную линейную регрессионную модель связи признаков Х и Y, используя инструмент Регрессия надстройки Пакет анализ.
1. Сервис => Анализ данных => Регрессия => ОК;
2. Входной интервал Y С4:С29;
3. Входной интервал X В4:В29;
4. Метки в первой строке/Метки в первом столбце – не активизировать;
5. Уровень надежности <= 68,3;
6. Константа–ноль – не активизировать;
7. Выходной интервал А81;
8. Новый рабочий лист и Новая рабочая книга – не активизировать;
9. Остатки – активизировать;
10. Стандартизованные остатки – не активизировать;
11. График остатков – не активизировать;
12. График подбора – активизировать;
13. График нормальной вероятности – не активизировать;
14. ОК.
В результате указанных действий осуществляется вывод в заданный диапазон рабочего файла четырех выходных таблиц и одного графика, начиная с ячейки, указанной в поле Выходной интервал:
Регрессионная статистика
| Регрессионная статистика |
| ||||
| Множественный R | 0.946358973 | ||||
| R-квадрат | 0.895595305 | ||||
| Нормированный R-квадрат | 0.891245109 | ||||
| Стандартная ошибка | 506.3202843 | ||||
| Наблюдения | 26 | ||||
| Дисперсионный анализ | |||||
|
| df | SS | MS | F | Значимость F |
| Регрессия | 1 | 52778090.51 | 52778090.51 | 205.8747195 | 2.84426E-13 |
| Остаток | 24 | 6152645.527 | 256360.2303 | ||
| Итого | 25 | 58930736.04 | |||
|
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение |
| Y-пересечение | -32.80047442 | 198.6470804 | -0.165119338 | 0.870232989 |
| Переменная X 1 | 2.292113652 | 0.159747709 | 14.34833508 | 2.84426E-13 |
| Нижние 95% | Верхние 95% | Нижние 68.3% | Верхние 68.3% |
| -442.7878952 | 377.1869463 | -235.8061414 | 170.2051925 |
| 1.962410588 | 2.621816716 | 2.128860862 | 2.455366443 |
| Наблюдение | Предсказанное Y | Остатки |
| 1 | 124.3009953 | 24.69900469 |
| 2 | 464.3589768 | 981.6410232 |
| 3 | 848.9985688 | -101.9985688 |
| 4 | 853.3306636 | 211.6693364 |
| 5 | 1512.267496 | -198.2674963 |
| 6 | 1573.375246 | -43.37524631 |
| 7 | 1647.410517 | 222.5894827 |
| 8 | 1704.644595 | 214.3554048 |
| 9 | 1796.008245 | 0.991754634 |
| 10 | 1833.965647 | -191.9656474 |
| 11 | 1884.804728 | -29.80472826 |
| 12 | 2028.176437 | -123.1764372 |
| 13 | 2047.086375 | -17.08637484 |
| 14 | 2152.86742 | -636.8674199 |
| 15 | 2234.856325 | 178.1436748 |
| 16 | 2471.333691 | 123.6663092 |
| 17 | 2485.292663 | 833.7073371 |
| 18 | 2509.42862 | -776.4286197 |
| 19 | 2706.940053 | -376.9400531 |
| 20 | 3087.362156 | -803.362156 |
| 21 | 3095.865898 | -465.8658976 |
| 22 | 3358.679649 | -176.679649 |
| 23 | 4484.955534 | -104.9555343 |
| 24 | 4937.258321 | 1347.741679 |
| 25 | 5493.554305 | -449.5543048 |
| 26 | 5993.876873 | 357.1231272 |
4. Оценить адекватность и практическую пригодность построенной линейной регрессионной модели, указав:
а) доверительные интервалы коэффициентов а0, а1;
а0: (-442.7878952; 377.1869463): для уровня надежности Р=0,95;а0: (-235.8061414; 170.2051925): для уровня надежности Р=0,683. а1: (1.962410588; 2.621816716): для уровня надежности Р=0,95; а1: (2.128860862; 2.455366443): для уровня надежности Р=0,683.
б) степень тесноты связи между признаками Х и Y;
Её можно определить по коэффициенту детерминации (см. табл. Регрессионная статистика): R-квадрат = 0.895595305. Это означает высокую степень тесноты связи признаков в уравнении регрессии, так как удовлетворяет условию R>0,7.
С помощью F - критерия Фишера можно определить значимость коэффициента детерминации R2.
FR= R2/(1- R2)*(n-m)/(m-1), где m – число групп областей. FR= (0,896/0,104)*6=51,69, что больше Fтабл=5,77 (к1=m-1, к2=n-m). Следовательно, коэффициент детерминации R2 значим, то есть зависимость между признаками X и Y регрессионной модели является статистически существенной, а значит, построенная модель в целом адекватна исследуемому процессу.
5. Дать экономическую интерпретацию:
а) коэффициента регрессии а1;
В нашей задаче коэффициент а1=2,292113652 (см. таблицы Регрессионная статистика) показывает, что результативный признак при изменении факторного увеличивается на данную величину.
б) коэффициента эластичности Кэ;
Данный коэффициент показывает, на сколько процентов изменяется в среднем результативный признак при изменении факторного на 1%. Кэ = а1*(![]() /
/![]() ) = 2,292*(1077,00/2435,81)=1,0134%. То есть результативный признак изменяется на 1,0134%.
) = 2,292*(1077,00/2435,81)=1,0134%. То есть результативный признак изменяется на 1,0134%.
в) остаточных величин ![]() i.
i.
Значения остатков имеют как положительные, так и отрицательные отклонения от ожидаемого уровня анализируемого показателя. Экономический интерес представляют области России: Архангельская, Курская, поскольку в них степень износа отличается наибольшими положительными отклонениями. То есть в данных областях стоимость основных фондов в отрасли – строительство наибольшая. А также Орловская и Костромская, то есть области, требующие особого внимания (наибольшие отрицательные остатки).
6. Найти наиболее адекватное уравнение регрессии с помощью средств инструмента Мастер диаграмм. Построить для этого уравнения теоретическую линию регрессии.
Построение регрессионных моделей осуществляется непосредственно на диаграмме рассеяния.
1.Выделить мышью диаграмму рассеяния, расположенную начиная с ячейки Е4.
2.Диаграмма => Добавить линию тренда;
3.Выбрать вкладку Тип, задать вид регрессионной модели – полином 2-го порядка;
4.Выбрать вкладку Параметры и выполнить действия:
1.Переключатель Название аппроксимирующей кривой: автоматическое/другое – установить в положение автоматическое;
2.Поле Прогноз вперед на – не активизировать;
3.Поле Прогноз назад на – не активизировать;
4.Флажок Пересечение кривой с осью Y в точке – не активировать;
5.Флажок Показывать уравнение на диаграмме – активизировать;
6.Флажок Поместить на диаграмму величину достоверности аппроксимации R2 – активизировать;
7.ОК;
8.Установить курсор на линию регрессии и щелкнуть правой клавишей мыши;
9.В появившемся диалоговом окне Формат линии тренда выбрать тип, цвет и толщину линии;
10.ОК;
11.Вынести уравнение и коэффициент R2 за корреляционное поле.
5.Действия 3 – 4 (в п.4 –шаги 1–11) выполнить поочередно для следующих видов регрессионных моделей: полином 3-го порядка, степенная, экспоненциальная.
Уравнения регрессии и их графики
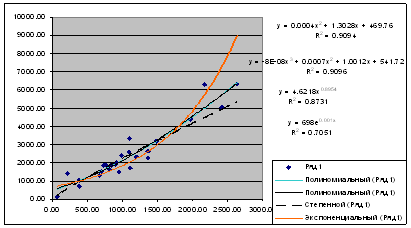
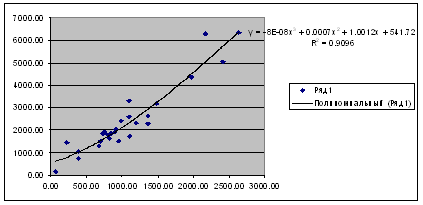
1.Теперь выберем наиболее адекватную регрессионную модель, то есть ту где больше коэффициент детерминации. В нашем случае это R2 =0,9096.
2.Выделить диаграмму рассеяния, расположенную с ячейки Е20;
3.Диаграмма => Добавить линию тренда;
4.Выбрать вкладку Тип и задать вид: полином 3-го порядка;
5.Выбрать вкладку Параметры:
1.Переключатель Название аппроксимирующей кривой: автоматическое/другое – установить в положение автоматическое;
2.Поле Прогноз вперед на – не активизировать;
3.Поле Прогноз назад на – не активизировать;
4.Флажок Пересечение кривой с осью Y в точке – не активировать;
5.Флажок Показывать уравнение на диаграмме – активизировать;
6.Флажок Поместить на диаграмму величину достоверности аппроксимации R2 – активизировать;
7.ОК.
Наиболее адекватное уравнение регрессии и его график
Заключение
В данной курсовой работе я рассмотрела тему «Статистика основных фондов», изучив предмет и методы данного раздела статистики, указав его показатели, а также статистические методы и их применение в изучении основных фондов. Всё это содержится в первой главе работы. Также я выполнила несколько расчётных задач, закрепив полученные данные. В аналитической части курсовой работы я освоила методики корреляционно-регрессионного анализа взаимосвязи социально-экономических явлений с применением компьютерных средств, так как изучение взаимосвязей явлений и процессов – одна из важнейших задач статистических исследований.
Данный метод позволяет:
· выявить наличие корреляционной связи признаков (показателей) и оценить ее тесноту;
· найти аналитическое выражение связи в виде уравнения регрессии;
· оценить качество найденной модели связи.
Для этого я использовала табличный процессор Microsoft Excel и его надстройку Пакет анализа, которые предоставляют ряд программных средств для автоматизированного решения вышеперечисленных задач.
Список использованной литературы
1. Гусаров В.М. Статистика: Учебное пособие для вузов. – М.: ЮНИТИ – ДАНА,2001. с.340 – 348.
2. Практикум по статистике: Учебное пособие для вузов / Под ред. проф. В.М. Симчеры. – Москва, ЗАО «Финстатинфом», 1999. с. 6 - 12.
3. Практикум по статистике: Учебное пособие для вузов / Под ред. Я.С. Мелкумова, 2004. с. 60 - 63
4. Социально – экономические показатели регионов России, 2006. с.369, 375.
5. Статистика: Учебник / Под ред. доктора экономических наук, профессора, члена – корреспондента РАН, Академика Международной Академии Наук высшей школы И.И. Елисеевой. – Москва, 2004. с. 244 – 253.
Похожие работы
... оцениваемого объекта определяется текущей стоимостью доходов, которые этот объект может принести своему собственнику. 2. СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ СОСТАВА, СТРУКТУРЫ И СОСТОЯНИЯ ОСНОВНЫХ ФОНДОВ. 2.1. Состав и структура основных фондов предприятия, анализ динамики. ОСНОВНЫЕ ФОНДЫ ПРЕДПРИЯТИЯ представляют ...
... нематериальных активов в учете и отчетности. Причина этого заключается как в объективной сложности самого понятия нематериальных активов, так и в отсутствии длительного опыта их отражения в российском учете. Поэтому предпринимаются попытки оценки общей стоимости нематериальных основных фондов на макроэкономическом уровне на основе данных о затратах на науку в части, образующей стоимость ...
... в результате изменения объема основных фондов и фондоотдачи осуществляется на основе индексов стоимостного объема производства, основных фондов и индекса фондоотдачи. 3. Применение балансового метода в изучении основных фондов 3.1 Статистические методы, используемые в изучении ОФ Основными методами являются сводка и группировка, обобщающие статистические показатели (выраженные абсолютными, ...
... , финансовые, обладает основными и оборотными средствами, что позволяет осуществлять хозяйству свою производственную деятельность. Глава 3. Статистический анализ состояния и использования основных фондов 3.1. Статистический анализ современного состояния основных фондов Количественную характеристику воспроизводства основных фондов в течение года дает следующее балансовое уравнение: Фк ...
0 комментариев