Основні властивості простору Соболєва

Реферат

Основні властивості простору Соболєва

Зміст

1. Простір Соболєва

1.1 Загальне визначення

1.2 Простір

1.3 Інше визначення узагальненої похідної

1.4 Найпростіша теорема вкладення

1.5 Простір Соболєва  й

2. Застосування просторів Соболєва в математичній фізиці

2.1 Доказ існування й одиничності узагальненого рішення рівняння Лапласа

Висновок

Список літератури

1. Простір Соболєва

1.1 Загальне визначення

Нехай у  задана замкнута обмежена область  Розглянемо лінійний простір речовинних функцій   раз безупинно диференцюємих на  Диференцюємость на замкнутій області  можна розуміти в різних змістах. Ми будемо припускати, що у  функції   раз безупинно диференцюємі, причому кожна частинна похідна функції  має межу при прагненні  до будь-якої граничної крапки області  так що в результаті її продовження на  вона стає безперервної в  Границя  області  передбачається досить гладкої. Крім того, звичайно ми будемо вважати область  одно зв'язковий і задовольняючому такому додатковому обмеженням, які можуть знадобитися в тих або інших міркуваннях.

Скористаємося для стислості наступними позначеннями. Набір індексів  називається мультиіндексом. Число  називається довжиною мультиіндекса. Для позначення часток похідних приймемо

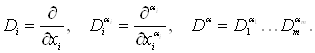
Уведемо в розглянутому вище лінійному просторі норму

(1.1)

Отриманий нормований простір позначається  Його поповнення в нормі (1.1) позначається  й називається простором Соболєва.

У прикладних задачах досить часто зустрічається випадок  Загальноприйнятий наступне позначення:  Простір Соболєва  є гильбертовим простором – поповненням простору  в нормі, породженої скалярним добутком

Нижче ми докладніше зупинимося на окремих випадках  і  тобто розглянемо простору Соболєва на речовинній осі й у тривимірному просторі.

1.2 Простір

Розглянемо на відрізку  простір  який складається із усіляких функцій  безупинно диференцюємих на  зі скалярним добутком

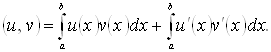(1.2)

і відповідному цьому скалярному добутку нормою

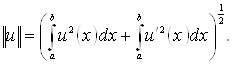(1.3)

 є поповненням  у цій нормі. Елементами  відповідно до теореми про поповнення, є класи, що складаються з послідовностей  фундаментальних в  у середньому, точніше, таких, що

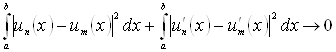 при

Дві такі послідовності  й  належать одному класу, якщо  є нескінченно малою по нормі  тобто, якщо

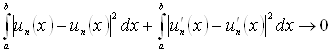 при

З умови фундаментальності в середньому  в  треба, що окремо при

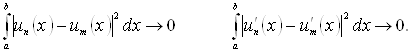
Аналогічно, з умови еквівалентності  й  по нормі  треба, що при

Відповідно до визначення простору  існують функції  й  такі, що при   а  в середньому.

Ми приходимо до наступного найважливішого визначення. Нехай  Тоді у  визначені елемент  із представником  і елемент  із представником   називається узагальненій похідній (у змісті Соболєва) від  При цьому пишуть:

З визначення узагальненій похідній  видно, що вона визначається не локально, в окремих крапках, а глобально – відразу на всім відрізку  Нехай  так що   Перейдемо до межі при  в рівностях

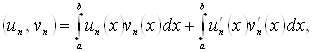(1.4)

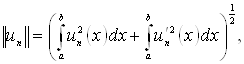(1.5)

і, відповідно до теореми про поповнення й визначення інтеграла Лебега, прийдемо до формул (1.2) і (1.3), де тепер похідні розуміються в узагальненому змісті, а інтеграл – у змісті Лебега. Для конкретних обчислень, зрозуміло, можна й потрібно користуватися формулами (1.4) і (1.5), взявши досить велике  тобто замість ідеальних елементів     скористатися їхніми гладкими наближеннями    

1.3 Інше визначення узагальненої похідної

Нехай  – множина всіх безупинно диференцюємих на відрізку  фінітних функцій  Якщо тепер  безупинно дференцюєма на відрізку  те для довільної функції  справедливо наступна інтегральна тотожність:

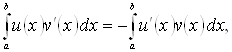(1.6)

перевіряється інтегруванням вроздріб. Цією тотожністю  повністю визначається.

Допустимо, що, крім того, для будь-яких  і деякої безперервної на відрізку  функції

(1.7)

Віднімаючи ці тотожності, одержимо, що для будь-яких

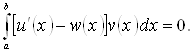
Звідси, внаслідок щільності  в   на відрізку  Виявляється, інтегральна тотожність (1.7) можна прийняти за визначення узагальненої похідної. Насамперед, справедлива наступна лема.

Лема 1. Якщо  то для будь-яких  справедливо тотожність (1.6).

Доказ. Нехай  тоді для всіх  маємо (1.6):

Внаслідок властивості безперервності скалярного добутку в останній рівності можна перейти до межі при  В результаті ми одержимо тотожність (1.6) для будь-якої функції  Лема доведена.

Лема 2. Нехай дані   такі, що для всіх  справедливо тотожність (1.7). Тоді  (узагальнена похідна).

Доказ. Нехай  а  Тоді

 

при

для будь-якого

Нехай  – клас, представником якого є

Тоді

 

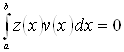
для будь-яких  Звідси  Лема доведена.