Застосування просторів Соболєва в математичній фізиці

2. Застосування просторів Соболєва в математичній фізиці

2.1 Доказ існування й одиничності узагальненого рішення рівняння Лапласа

 

Теорема 3 (Рисс). Нехай  – гильбертовий простір. Для будь-якого лінійного обмеженого функціонала  заданого всюди на  існує єдиний елемент  такий, що для всіх  

При цьому

Доказ наведений в [1, стор. 171].

Теорема Рисса ефективно застосовується в теорії можливості розв'язання граничних задач для рівнянь із частками похідними. Будемо говорити, що гильбертовий простір  вкладений у гильбертовий простір  якщо із  треба, що  причому існує постійна  така, що для всіх

(2.1)

Має місце наступний наслідок з теореми Рисса.

Теорема 4. Якщо гильбертовий простір  вкладений у гильбертовий простір  то для кожного елемента  найдеться єдиний елемент  такий, що для всіх  має місце тотожність

Тотожність це визначає оператор  такий, що  при цьому

Доказ. При кожному фіксованому  вираження  при всіляких  визначає лінійний обмежений функціонал на  Лінійність функціонала очевидна. Його обмеженість випливає з оцінки

По теоремі Рисса існує єдиний елемент  такий, що  Тим самим усюди на  заданий лінійний оператор  Далі, з доведеного вище нерівності треба, що

Думаючи тут  одержимо  тобто  й, виходить,  обмежений. Теорема доведена.

Як додаток доведеної теореми й просторів Соболєва доведемо існування й одиничність узагальненого рішення задачі Дирихле для рівняння Пуассона. У замкнутої обмеженої однозв'язної області  з досить гладкою границею  розглянемо наступну граничну задачу:

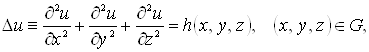(2.2)

(2.3)

Припустимо, що права частина  безперервна в  по сукупності змінних. Функція  називається класичним рішенням задачі (2.2) – (2.3), якщо  безперервно як функцію трьох змінних у  має в  безперервні похідні, що входять у ліву частину (2.2), задовольняє в  рівнянню (2.2) і дорівнює нулю на  тобто задовольняє граничній умові (2.3).

Нехай  – класичне рішення задачі (2.2) – (2.3), а  безперервна в  дорівнює нулю на  й безупинно дференцюєма в  тоді для будь-який такий  справедливо наступна інтегральна тотожність:

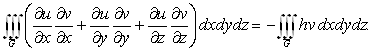(2.4)

Для доказу цієї тотожності скористаємося формулою Гаусса-Остроградського:

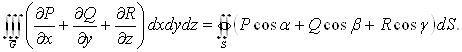
Приймемо

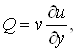
   й одержимо

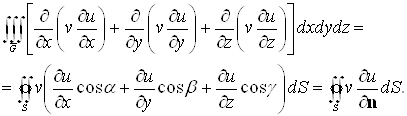
Оскільки

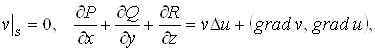
а  те одержуємо (2.4).

Нехай тепер   а інтеграли (2.4) розуміються в змісті Лебега. Функція  називається узагальненим рішенням крайової задачі (2.2) – (2.3), якщо для будь-якої функції  виконується інтегральна тотожність (2.4).

Доведемо, що для будь-якої правої частини  узагальнене рішення крайової задачі (2.2) – (2.3) існує і єдино.

Для цього помітимо, що гильбертовий простір  вкладений у гильбертовий простір  тому що, по визначенню  всяка функція  належить також і  й справедлива оцінка для кожної  (див. п. 1.5):

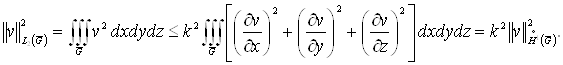
Отже, по теоремі 4 для всякої функції  існує єдина функція  така, що для всіх

а це і є інтегральну тотожність (2.4).

Висновок

Простір Соболєва  й тісно пов'язане з ним поняття узагальненої похідної в сенсі Соболєва були уведені в математичну практику академіком С.Л. Соболєвим і відіграють найважливішу роль у теоретичних і прикладних питаннях математичної фізики й функціонального аналізу. Поповнення простору гладких функцій  деякими ідеальними елементами, які можна з будь-яким ступенем точності обчислити за допомогою елементів із  приводить, з одного боку, внаслідок повноти  до точності й закінчення багатьох математичних тверджень, а з іншого боку, зберігає всі обчислювальні можливості.

Таким чином, ми розглянули простори Соболєва, їхні основні властивості й застосування в математичній фізиці.

Список літератури

1. Треногін В.О. Функціональний аналіз. – К., 2006

2. Соболєв С.Л. Деякі застосування функціонального аналізу в математичній фізиці. – К, 2004

3. Куланін Е.Д., Норін В.П. 3000 конкурсних задач по математиці. – К., 2000

4. Гусєв В.А., Мордкович А.Д. Довідкові матеріали по математиці. – К., 2003

5. Сканаві М.М. Збірник задач по математиці. – К., 2006