Навигация
Дифференцирование в линейных нормированных пространствах
Министерство образования и науки Российской федерации
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
Тюменский государственный университет
Институт математики и компьютерных наук
Кафедра информатики и математики
КУРСОВАЯ РАБОТА
По дисциплине «Математический анализ»
на тему:
Дифференцирование в линейных нормированных пространствах
Выполнила: студентка 393 гр.
Жукова И.А.
Проверил: доцент кафедры МиИ
Салтанова Т.В.
Тюмень 2010
Оглавление
Введение
Основные понятия
Сильный дифференциал (дифференциал Фреше)
Слабый дифференциал (дифференциал Гато)
Формула конечных приращений
Связь между слабой и сильной дифференцируемостью
Дифференцируемые функционалы
Абстрактные функции
Интеграл
Производные высших порядков
Дифференциалы высших порядков
Формула Тейлора
Заключение1
Список литературы:
Введение
Функциональный анализ — раздел математики, в котором изучаются бесконечномерные пространства и их отображения.
Понятие нормированного пространства – одно из самых основных понятий функционального анализа. Теория нормированных пространств была построена, главным образом, С. Банахом в 20-х годах 20 века. Функциональный анализ за последние два десятилетия настолько разросся, настолько широко и глубоко проник почти во все области математики, что сейчас даже трудно определить самый предмет этой дисциплины. Однако в функциональном анализе есть несколько больших «традиционных» направлений, которые и поныне в значительной степени определяют его лицо. К их числу принадлежит дифференцирование линейных нормированных пространств.
Основные понятия
Определение 1. Непустое множество ![]() называется линейным пространством, если оно удовлетворяет следующим условиям:
называется линейным пространством, если оно удовлетворяет следующим условиям:
Й. Для любых двух элементов ![]() однозначно определен элемент
однозначно определен элемент ![]() , называемый их суммой, причем
, называемый их суммой, причем
1. ![]() (коммутативность)
(коммутативность)
2. ![]() (ассоциативность)
(ассоциативность)
В ![]() существует такой элемент 0, что
существует такой элемент 0, что ![]() для всех
для всех ![]()
4. Для каждого ![]() существует такой элемент
существует такой элемент ![]() , что
, что ![]() .
.
II. Для любого числа ![]() и любого элемента
и любого элемента ![]() определен элемент
определен элемент ![]() , причем
, причем
5. ![]()
6. ![]()
III. Операции сложения и умножения связаны между собой дистрибутивными законами:
7. ![]()
8. ![]()
Определение 2. Линейное пространство ![]() называется нормированным, если на нем задана неотрицательная функция
называется нормированным, если на нем задана неотрицательная функция ![]() , называемая нормой, удовлетворяющая условиям:
, называемая нормой, удовлетворяющая условиям:
![]()
![]()
для любого ![]() и любого числа
и любого числа ![]() ;
;
![]()
для любых ![]() (неравенство треугольника).
(неравенство треугольника).
Определение 3. Оператором называется отображение
![]() ,
,
где ![]() - это линейные пространства.
- это линейные пространства.
Определение 4. Оператор ![]()
![]() называется линейным, если для любых элементов
называется линейным, если для любых элементов ![]() и любых чисел
и любых чисел ![]() R выполняется равенство:
R выполняется равенство:
![]()
Определение 5. Пусть ![]() - линейные нормированные пространства,
- линейные нормированные пространства,
![]()
![]() – линейный оператор,
– линейный оператор,
![]()
Линейный оператор непрерывен в точке ![]() , если из того, что
, если из того, что
![]() следует, что
следует, что ![]() .
.
Определение 6. Линейный оператор ![]() непрерывен, если он непрерывен в каждой точке
непрерывен, если он непрерывен в каждой точке ![]() .
.
Определение 7. Линейный оператор называется ограниченным, если
![]()
![]()
![]()
Утверждение. Для линейного нормированного пространства непрерывность линейного оператора равносильна его ограниченности.
Определение8. Наименьшая из констант M таких, что ![]() , называется нормой оператора А и обозначается
, называется нормой оператора А и обозначается ![]() .
.
В частности, выполняется
![]()
Справедливо следующее утверждение: для любого ограниченного линейного оператора
![]()
![]()
Пусть X и У — два нормированных пространства и F — отображение, действующее из X в Y и определенное на некотором открытом подмножестве О пространства X. Мы назовем это отображение дифференцируемым в данной точке![]() , если существует такой ограниченный линейный оператор Lx
, если существует такой ограниченный линейный оператор Lx![]() ж (X, Y), что для любого е> 0 можно найти д > 0, при котором из неравенства ||h||< д следует неравенство
ж (X, Y), что для любого е> 0 можно найти д > 0, при котором из неравенства ||h||< д следует неравенство
|| F(x + h)-F(x)-Lxh ||<е||h|| (1)
То же самое сокращенно записывают так:
А(ч + р)-А(ч)-Дчр = щ(р)ю(2)
Из (I) следует, что дифференцируемое в точке х отображение непрерывно в этой точке. Выражение Lxh (представляющее собой, очевидно, при каждом h![]() X элемент пространства У) называется сильным дифференциалом (или дифференциалом Фреше) отображения F в точке х. Сам линейный оператор Lxназывается производной, точнее, сильной производной отображения F в точке х. Мы будем обозначать эту производную символом F'(x).
X элемент пространства У) называется сильным дифференциалом (или дифференциалом Фреше) отображения F в точке х. Сам линейный оператор Lxназывается производной, точнее, сильной производной отображения F в точке х. Мы будем обозначать эту производную символом F'(x).
Если отображение F дифференцируемо в точке, то соответствующая производная определяется единственным образом. В самом деле, равенство
||L1h — L2h|| = o(h) для операторов
Li![]() ж (X, У), i = 1, 2,
ж (X, У), i = 1, 2,
возможно, лишь если L1= L2.
Установим теперь некоторые элементарные факты, непоcредственно вытекающие из определения производной.
Если F(x) = y0 = const, то F'(x) = О (т. е. F'(х)
в этом случае есть нулевой оператор).
Производная непрерывного линейного отображения L есть само это отображение:
L '(x)=L (3)
Действительно, по определению имеем
L(x + h)-L(x) = L(h).
3. (Производная сложной функции). Пусть X, У, Z — три нормированных пространства, U(x0)—окрестность точки х0![]() Х, F — отображение этой окрестности в У, у0 = F(x0), V(yo) — окрестность точки у0
Х, F — отображение этой окрестности в У, у0 = F(x0), V(yo) — окрестность точки у0![]() У и G — отображение этой окрестности в Z. Тогда, если отображение F дифференцируемо в точке хо, a G дифференцируемо в точке уо, то отображение Н = GF (которое определено в некоторой окрестности точки х0) дифференцируемо в точке хо и
У и G — отображение этой окрестности в Z. Тогда, если отображение F дифференцируемо в точке хо, a G дифференцируемо в точке уо, то отображение Н = GF (которое определено в некоторой окрестности точки х0) дифференцируемо в точке хо и
H' (x0)=G' (y0)F' (x0) (4)
Действительно, в силу сделанных предположений
А(ч0 +о) = А(ч0) + Аэ (ч0) о +о1 (о ) и
G (уо + з) = G (уо) + G' (уо) з + о2 (з).
Но F'(x0) и G'(yo) — ограниченные линейные операторы. Поэтому
H (х0 + о) = G (уо + F' (x0) о + о1 о ) = G (уо) + G' (у0) (F' (х0) о + +о1 о)) +
+о2 (F' (x0) о + о1 (о )) = G (у0) + G' (уо) F' (х0) о + о3 (о).
Если F, G и Н — числовые функции, то формула (4) превращается в известное правило дифференцирования сложной функции.
4. Пусть F и G — два непрерывных отображения, действующих из X в Y. Если F и G дифференцируемы в точке х0, то и отображения F + G и aF (а — число) тоже дифференцируемы в этой точке, причем
(F + G)'(х0) = F'(х0) + G'(х0) (5)
(aF)'(x0) = aF'(x0).(6)
Действительно, из определения суммы операторов и произведения оператора на число сразу получаем, что
(F+G)(x0 + h) = F(x0 + h) + G(x0 + h) = F (х0) + G (х0) + F' (х0) h +
+G' (х0) h + o1 (h) и
aF (x0 + h) = aF (x0) + aF' (x0) h + o2 (h),
откуда следуют равенства (5) и (6).
Слабый дифференциал (дифференциал Гато)Пусть снова F есть отображение, действующее из X в У. Слабым дифференциалом или дифференциалом Гато отображения F в точке х (при приращении h) называется предел
DF(x,h)=![]() t=0=
t=0=![]()
![]()
![]() ,
,
где сходимость понимается как сходимость по норме в пространстве У.
Иногда, следуя Лагранжу, выражение DF(x,h) называют первой вариацией отображения F в точке х.
Слабый дифференциал DF(x,h) может и не быть линеен по h. Если же такая линейность имеет место, т. е. если
DF (х, h) = F'c (х) h,
где F'c (х) — ограниченный линейный оператор, то этот оператор называется слабой производной (или производной Гато).
Заметим, что для слабых производных теорема о дифференцировании сложной функции, вообще говоря, неверна.
Формула конечных приращенийПусть О — открытое множество в X и пусть отрезок [х0, х] целиком содержится в О. Пусть, наконец, F есть отображение X в У, определенное на О и имеющее слабую производную F'c в каждой точке отрезка [х0, x]. Положив Дх = х — хо и взяв произвольный функционал ![]() У*, рассмотрим числовую функцию
У*, рассмотрим числовую функцию
f(t) = ![]() (F(x0+t Дх)),
(F(x0+t Дх)),
определенную при ![]() .Эта функция дифференцируема по t. Действительно, в выражении
.Эта функция дифференцируема по t. Действительно, в выражении
![]()
можно перейти к пределу под знаком непрерывного линейного функционала![]() . В результате получаем
. В результате получаем
F'(t) = ![]() (F'c(x0+tДx) Дx)
(F'c(x0+tДx) Дx)
Применив к функции f на отрезке [0, 1] формулу конечных приращений, получим
f(l) = f(0) + f'(и), где 0< и <1,
![]() (F(x)-F(x0))=
(F(x)-F(x0))= ![]() ( F'c(x0+ и Дx) Дx)(7)
( F'c(x0+ и Дx) Дx)(7)
Это равенство имеет место для любого функционала ![]() У* (величина и зависит, разумеется, от
У* (величина и зависит, разумеется, от![]() ). Из (7) получаем
). Из (7) получаем
|![]() (F(x)-F(x0))|
(F(x)-F(x0))|![]()
![]()
![]() || F'c(x0+ и Дx)||
|| F'c(x0+ и Дx)|| ![]() || Дx|| (8)
|| Дx|| (8)
Выберем теперь ненулевой функционал ![]() так, что
так, что
![]() (F (х) - F (х0)) = ||
(F (х) - F (х0)) = ||![]() ||
|| ![]() || F (х) - F (хо) ||
|| F (х) - F (хо) ||
(такой функционал ![]() существует в силу следствия 4 теоремы Хана — Банаха (см. п. 3 § 1 гл. IV)). При этом из (8) получаем
существует в силу следствия 4 теоремы Хана — Банаха (см. п. 3 § 1 гл. IV)). При этом из (8) получаем
||(F (х) - F (x)||![]()
![]() || F'c(x0+ и Дx)||
|| F'c(x0+ и Дx)|| ![]() ||Дx|| (Дx =x-x0) (9)
||Дx|| (Дx =x-x0) (9)
Это неравенство можно рассматривать как аналог формулы конечных приращений для числовых функций. Применив формулу (9) к отображению
х —Ю А (х) — Аэс (хо) Дч
получим следующее неравенство:
||F(x-F(хо)-F'c (хо) Дx || ![]()
![]() || F'c(xo+иДx) -F'c(x0) ||
|| F'c(xo+иДx) -F'c(x0) ||![]() || Дx || (10)
|| Дx || (10)
Связь между слабой и сильной дифференцируемостью
Сильная и слабая дифференцируемость представляют собой различные понятия даже в случае конечномерных пространств. Действительно, из анализа хорошо известно, что для числовой функции
f(x) = f(x1,…,xn)
при n
Похожие работы
... непрерывных и ограниченных функций – C[], заданный следующим образом: Af(x) = f(x+a). Функции f(x), f(x+a) C[], a R, f(x+a) – непрерывная и ограниченная функция. Покажем линейность оператора А, по определению 1 должны выполняться следующие аксиомы : 1) Аксиома аддитивности: А(f+g) = А(f) + А(g). А(f+g) = (f+g)(x+a) = f(x+a) + g(x+a) = А(f) + А(g). По определению суммы функции, аксиома ...
... , называется оператором сдвига, если он каждую последовательность вида (х1,х2,…, хn…) переводит в последовательность вида (0, х1, х2, …, хn…), т.е. выполняется равенство: (х1,х2,…, хn…)=(0, х1, х2, …, хn…). Можно также рассматривать оператор сдвига, который действует в пространстве последовательностей, бесконечных в обе стороны. Элемент этого пространства можно представить в таком виде: (…х-2, ...
... [a,b]. Теперь мы можем рассматривать функции в произвольных нормированных пространствах. III. Методы аппроксимации 3.1 Приближение функций многочленами. Алгебраическим многочленом степени n называется функция - действительные числа, называемые коэффициентами. Алгебраические многочлены являются простейшими функциями. Они непрерывны при любом x. Производная многочлена- так же многочлен, степень ...
... несколько уравнений, а в каждом уравнении - несколько переменных. Задача оценивания параметров такой разветвленной модели решается с помощью сложных и причудливых методов. Однако все они имеют одну и ту же теоретическую основу. Поэтому для получения начального представления о содержании эконометрических методов мы ограничимся в последующих параграфах рассмотрением простой линейной регрессии. ...
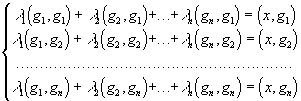
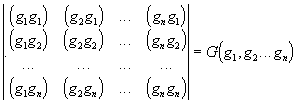
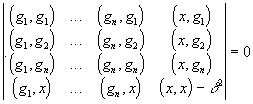
0 комментариев