Навигация
Существует такое положительное число М, что
2. существует такое положительное число М, что
||В(х, х') || ![]() M||x||
M||x||![]() ||x’|| (17)
||x’|| (17)
при всех х, х'![]() X.
X.
Первое из этих условий означает, что отображение В линейно по каждому из двух своих аргументов; нетрудно показать, что второе условие равносильно непрерывности В по совокупности аргументов.
Наименьшее из чисел М, удовлетворяющих условию (17), называется нормой билинейного отображения В и обозначается ||В||.
Линейные операции над билинейными отображениями определяются обычным способом и обладают обычными свойствами.
Таким образом, билинейные отображения пространства X в пространство У сами образуют линейное нормированное пространство, которое мы обозначим В(Х2, У). При полноте У полно и В(Х2, У).
Каждому элементу А из пространства о(Х,о(Х,У)) можно поставить в соответствие элемент из В(Х2, У), положив
В(х, х') = (Ах)х'.(18)
Очевидно, что это соответствие линейно. Покажем, что оно также и изометрично и отображает пространство о(X,о(Х,У)) на все пространство B(X2,Y). Действительно, если у=В(х, х') = (Ах)х', то
||y||![]() ||Ax||
||Ax||![]() ||x’||
||x’||![]() ||A||
||A||![]() ||x||
||x||![]() ||x’||,
||x’||,
откуда
||B||![]() ||A||(19)
||A||(19)
С другой стороны, если задано билинейное отображение В, то при фиксированном x![]() Xотображение
Xотображение
х'→ (Ах)х' = В(х, х')
есть линейное отображение пространства X в У.
Таким образом, каждому x![]() X ставится в соответствие элемент Ах пространства о(X, У); очевидно, что Ах линейно зависит от х, т. е. билинейное отображение В определяет некоторый элемент А пространства о(Х, о(Х, У)). При этом ясно, что отображение В восстанавливается по А при помощи формулы (18) и
X ставится в соответствие элемент Ах пространства о(X, У); очевидно, что Ах линейно зависит от х, т. е. билинейное отображение В определяет некоторый элемент А пространства о(Х, о(Х, У)). При этом ясно, что отображение В восстанавливается по А при помощи формулы (18) и
||Ах||= ![]() ||(Ax)x'||=
||(Ax)x'||=![]() ||В(х,x')
||В(х,x') ![]() ||B||
||B|| ![]() ||x||,
||x||,
Откуда
||A||![]() ||B||(20)
||B||(20)
Сопоставляя (19) и (20), получаем||A|| = ||В||. Итак, соответствие между B(X2,Y) и о{X, о(X,Y)), определяемое равенством (18), линейно и изометрично, а следовательно, взаимно однозначно. При этом образ пространства о(Х, о(Х, У)) есть все В(Х2, У).
Мы выяснили, что вторая производная F"(x) есть элемент пространства о(X, о (X, У)). В соответствии с только что сказанным мы можем считать F"(x) элементом пространства В(Х2, Y).
Очевидным образом можно ввести понятие третьей, четвертой и вообще п-й производной отображения F, действующего из X в Y, определив п-ю производную как производную от производной (п—1)-го порядка. При этом, очевидно, п-я производная представляет собой элемент пространства о(Х, о(Х, ..., о(X, У))). Повторяя рассуждения, проведенные для второй производной, можно каждому элементу этого пространства естественным образом поставить в соответствие элемент пространства N(Хп, У) n-линейных отображений X в У.
При этом под n-линейным отображением понимается такое соответствие y=N(x', х", ..., x(n)) между упорядоченными системами (х', х", .. . , x(n)) элементов из X и элементами пространства У, которое линейно по каждому из хi при фиксированных остальных элементах и удовлетворяет при некотором М > 0 условию
|| N (x', х", ..., x(n)) ||![]() М || х' || • || х" || ... || x(n) ||.
М || х' || • || х" || ... || x(n) ||.
Таким образом, п-ю производную отображения F можно считать, элементом пространства N(Xn, У).
Дифференциалы высших порядковМы определили (сильный) дифференциал отображения F как результат применения к элементу h![]() Х линейного оператора F'(x), т. е.
Х линейного оператора F'(x), т. е.
dF = F'(x)h
Дифференциал второго порядка определяется как
d2F = F" (х) (h, h),
т. е. как квадратичное выражение, отвечающее отображению
F''(х) ![]() В(X2, У)
В(X2, У)
Аналогично дифференциалом п-го порядка называется
dnF=F(n)(x)(h, h, h),
т. е. тот элемент пространства У, в который элемент (h, h, ..., h) ![]()
![]() переводится отображением F(n)(x).
переводится отображением F(n)(x).
Формула Тейлора
Сильная дифференцируемость отображения F означает, что разность
F(x+h)—F(x)
может быть представлена в виде суммы линейного члена и слагаемого, имеющего порядок выше первого относительно ||h||. Обобщением этого факта является формула, аналогичная формуле Тейлора для числовых функций.
Теорема 2. Пусть F — отображение, действующее из X в У, определенное в некоторой области О![]() X и такое, что F(n)(x) существует и представляет собой равномерно непрерывную функцию от х в О. Тогда имеет место равенство
X и такое, что F(n)(x) существует и представляет собой равномерно непрерывную функцию от х в О. Тогда имеет место равенство
f(x + h)-F(x) = F'(x)h + ![]() F"(x)(h, h)+ ...
F"(x)(h, h)+ ...
... +![]() F(n)(x)(h,…,h) + щ (х, h), (21)
F(n)(x)(h,…,h) + щ (х, h), (21)
где
![]()
Доказательство будем вести по индукции. При n = 1 равенство (21) тривиально. Возьмем теперь произвольное фиксированное n и предположим, что равенство, получающееся из (21) заменой n на n-1, уже доказано для всех отображений, удовлетворяющих условиям теоремы, в которых n заменено на п-1. Тогда для отображения F' имеем
F'(x + h) = F'(x) + F"(x)h +![]() F"'(x)(h,h) + ...
F"'(x)(h,h) + ...
… + ![]() F(n)(x)(h,…,h) + щ1 (х, h), (22)
F(n)(x)(h,…,h) + щ1 (х, h), (22)
где
||щ1 (х, h)|| = o(||h||n-1)
Интегрируя обе части равенства (22) по отрезку [х, x+h] и пользуясь формулой Ньютона — Лейбница (15), мы получим
![]()
![]() , (21)
, (21)
Где
![]() .
.
из (23) получаем
А(ч+ р)-А (х)= Аэ(ч)р + ![]() АЭ(ч)(рбр)+ ююю
АЭ(ч)(рбр)+ ююю
…+![]() F(n)(x)(h,…,h) + Rn, причем
F(n)(x)(h,…,h) + Rn, причем
||Rn||![]()
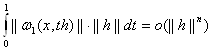
Тем самым наше утверждение доказано.
Формулу (21) называют формулой Тейлора для отображений.
Заключение
В этой работе представлены некоторые первоначальные понятия , относящиеся к нелинейному функциональному анализу, в основном к теории дифференцирования, и некоторые применения этих понятий.
Некоторые задачи, возникающие в функциональном анализе, носят существенно нелинейный характер; они приводят к необходимости развивать наряду с «линейными» и « нелинейными» функциональный анализ, т.е изучать нелинейные функционалы и нелинейные операторы в бесконечномерных пространствах.
К нелинейному функциональному анализу относится, по существу, такая классическая область математики, как вариационное исчисление, основы которого были заложены еще в XVII-XVIII вв. в работах Бернулли, Эйлера, Лагранжа. Однако в целом нелинейный функциональный анализ представляет собой сравнительно новую область математики, пока еще далекую от своего завершения.
Список литературы:
1. Колмогоров А.Н., Фомин С.В. - Элементы теории функций и функционального анализа. М., Наука, 1981. – 475 с.
2. Шилов Г.Е. – Дифференцирование функций в линейном пространстве. Ярославль, 1978. – 118стр.
3. Банах С. – Дифференциальное и интегральное исчисление. М.,Наука, 1972. – 424стр.
Похожие работы
... непрерывных и ограниченных функций – C[], заданный следующим образом: Af(x) = f(x+a). Функции f(x), f(x+a) C[], a R, f(x+a) – непрерывная и ограниченная функция. Покажем линейность оператора А, по определению 1 должны выполняться следующие аксиомы : 1) Аксиома аддитивности: А(f+g) = А(f) + А(g). А(f+g) = (f+g)(x+a) = f(x+a) + g(x+a) = А(f) + А(g). По определению суммы функции, аксиома ...
... , называется оператором сдвига, если он каждую последовательность вида (х1,х2,…, хn…) переводит в последовательность вида (0, х1, х2, …, хn…), т.е. выполняется равенство: (х1,х2,…, хn…)=(0, х1, х2, …, хn…). Можно также рассматривать оператор сдвига, который действует в пространстве последовательностей, бесконечных в обе стороны. Элемент этого пространства можно представить в таком виде: (…х-2, ...
... [a,b]. Теперь мы можем рассматривать функции в произвольных нормированных пространствах. III. Методы аппроксимации 3.1 Приближение функций многочленами. Алгебраическим многочленом степени n называется функция - действительные числа, называемые коэффициентами. Алгебраические многочлены являются простейшими функциями. Они непрерывны при любом x. Производная многочлена- так же многочлен, степень ...
... несколько уравнений, а в каждом уравнении - несколько переменных. Задача оценивания параметров такой разветвленной модели решается с помощью сложных и причудливых методов. Однако все они имеют одну и ту же теоретическую основу. Поэтому для получения начального представления о содержании эконометрических методов мы ограничимся в последующих параграфах рассмотрением простой линейной регрессии. ...
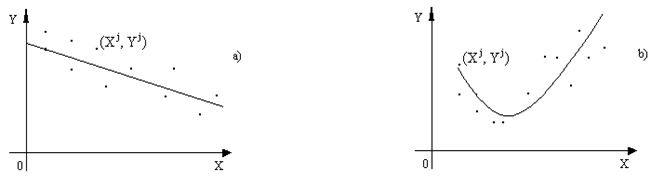
0 комментариев