Риски, связанные с вложением капитала (инвестиционные риски)
Риск-менеджмент. Финансовые риски как объект управления
Подходы к управлению (снижению и уменьшению) финансовыми рисками: лимитирование, диверсификация, страхование
Подходы к управлению (снижению и уменьшению) финансовыми рисками: управление активами и пассивами, хеджирование
Кривые безразличия
Диверсификация финансовых активов. Рыночный и собственный риск портфеля
Особенности управления финансовыми рисками облигаций
Как правило, величина премии за отзыв с каждым годом сокращается по мере приближения ко дню погашения
Ожидаемая доходность по облигации может быть сравнима с известной доходностью по бумаге, не имеющей риска неплатежа (государственной ценной бумаге)
Навигация
Кривые безразличия
Понятие и характеристики финансовых рисков. Методы оценки риска
70551
знак
6
таблиц
1
изображение
11. Кривые безразличия
Теория портфеля (Г. Марковец) связана с построением кривых безразличия, которые отражают отношение инвестора к риску и доходности.
| А | B | C | D | |
| rp | 8 | 12 | 11 | 7 |
| σp | 10 | 20 | 13 | 17 |
Каждая кривая линия на графике отображает одну кривую безразличия и представляет все комбинации портфеля, которые обеспечивают заданный уровень желания инвестора.
Свойства кривых безразличия:
1. Все портфели, лежащие на данной кривой безразличия являются равноценными для инвестора.
2. Кривые безразличия не могут пересекаться, т.к. они отражают разные уровни желательности.
3. Инвестор будет считать любой портфель, лежащий на кривой безразличия, которая находится выше и левее, привлекательнее, чем любой портфель, лежащий на кривой безразличия, расположенный ниже и правее.
4. Как бы не были расположены две кривые безразличия на графике, всегда существует возможность построить третью кривую, лежащую между ними.
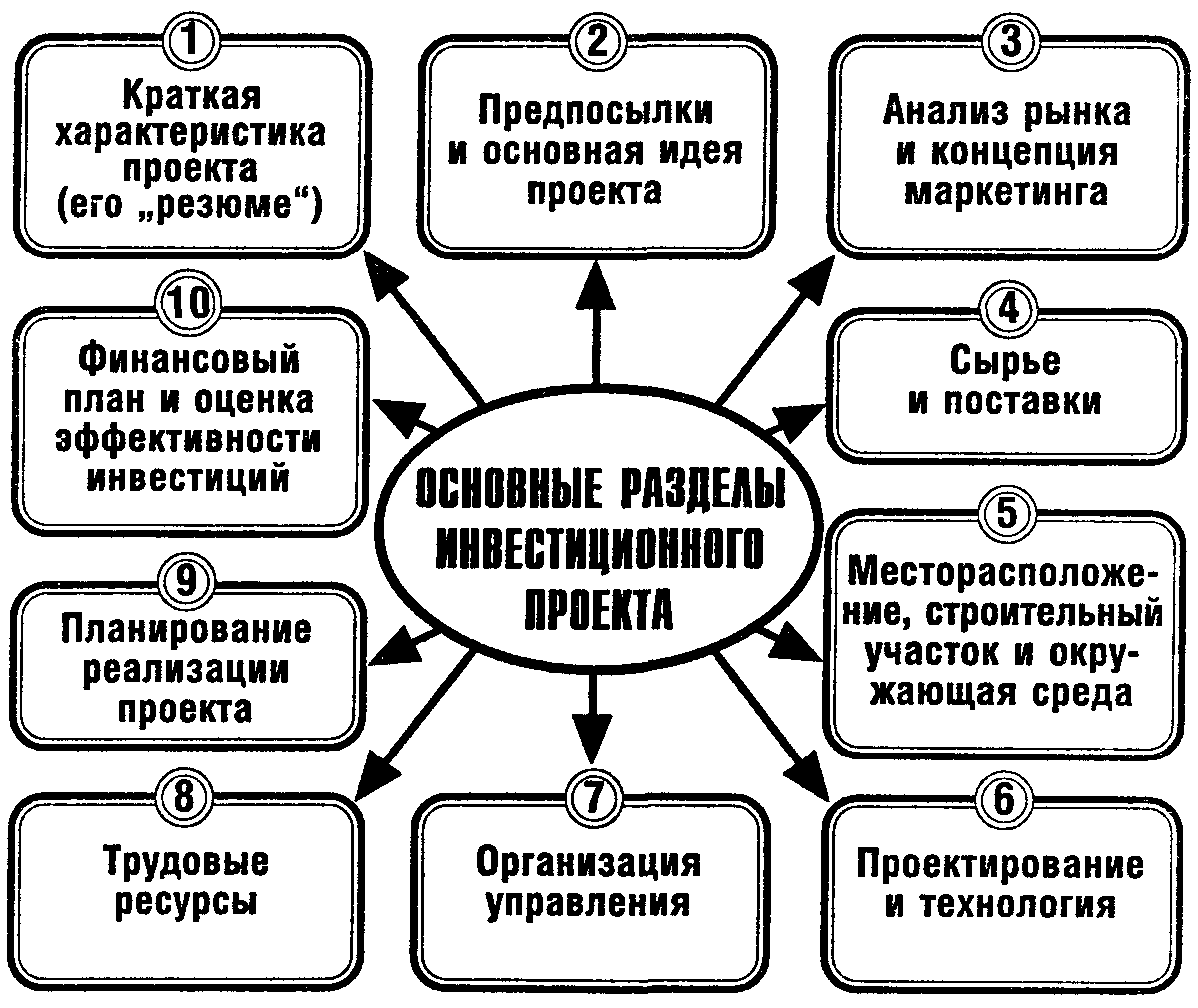
12. Портфельный анализ или выбор оптимального портфеля финансовых активов
Так существует бесконечное число возможных инвестиционных портфелей, возникает вопрос о выборе из этого множества самого оптимального портфеля.
Теореме об эффективном множестве
Инвестор выберет свой оптимальный портфель из множества портфелей, каждый из которых:
- обеспечивает максимальную ожидаемую доходность для некоторого уровня риска;
- обеспечивает минимальный риск для некоторого значения ожидаемой доходности.
Набор портфелей, удовлетворяющих этим двум условиям, называется эффективным множеством.
Для того чтобы найти эффективное множество, первоначально определяют достижимое множество.
Достижимое множество – представляет собой все портфели, которые могут быть сформированы из группы в N финансовых активов.
Не существует мене рисковых портфелей, чем портфель Е. Следовательно, не существует портфелей с большей ожидаемой доходностью, чем портфель S.
Е – min σp
S – max rp
H – max σp
G – min rp
Учитывая, что оба условия должны приниматься во внимание при определении эффективного множество, отметим, что этому удовлетворяют только портфели, лежащие на верхней и левой границе достижимого множества, между точками E и S.
Инвестор, владелец актива выбирает оптимальный портфель, который лежим (совмещается) с эффективным множеством портфелей.
Существует только одна точка касания эффективного множества и кривых безразличия данного инвестора, т.е. существует только один оптимальный портфель активов.
13. Рыночная модель поведения финансового актива
Предположим, что доходность финансового актива за данный период времени связана с доходностью за данный период акций на рыночный индекс (ММВБ, Доу Джонс).
Одним из путей отражения данной взаимосвязи является рыночная модель:
,
где ri – доходность финансового актива (ценной бумаги) за данный период;
rI – доходность на рыночный индекс I за этот же период;
αiI– коэффициент смещения;
βiI – коэффициент наклона;
εiI – случайная погрешность.
Если βiI> 0 из уравнения можно заметить следующее: чем выше доходность на рыночный индекс, тем выше доходность финансового актива (ценной бумаги).
Пример:
Акции А, для которых αiI = 2%, βiI = 1,2%,
rA = 2% + 1,2% rI + εiI
Если rI = 10% , то rA = 2% + 1,2% 10% + εiI= 14% + εiI
Среднее значение ожидаемой погрешности равно 0.
Если rI = -5% => rA= -4% + εiI
Случайная погрешность просто показывает, что рыночная модель не очень точно объясняет доходности ценных бумаг.
Разность между действительным и ожидаемым значением доходности финансового актива при известной доходности рыночного индекса приписывается случайной погрешности.
Графическое представление рыночной модели (рис. 1):
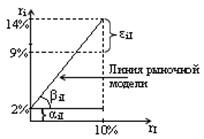
Рис. 1
Наклон (βiI) у рыночной модели финансового актива измеряет чувствительность его доходности к доходности на рыночный индекс.
Разный наклон показывает разные чувствительности к индексу.
,
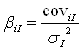где coviI– показывает ковариацию между доходностью актива i и доходностью на рыночный индекс;
σI – дисперсия доходности на индекс.
Актив, который имеет доходность, являющуюся зеркальным отражением доходности на индекс, будет иметь βiI = 1, т.е. активы с β-коэффициентом > 1 обладают большей изменчивостью, чем индекс и определяются как агрессивные активы. И наоборот, если βiI < 1 – меньшая изменчивость, чем индекс и активы называют оборонительными.
Похожие работы
... и на транспортные услуги и т.п. Внутренние факторы связаны с ошибками и упущениями руководства и персонала, с их готовностью к выбору рисковой стратегии в деятельности предприятия. 2. Статистические методы оценки риска Известны два вида анализа рисков: качественный и количественный. Качественный анализ дает возможность определить факторы и потенциальные области риска, выявить его виды. ...
... а именно: оценку рисков по контрольным точкам финансово-хозяйственной деятельности. Использование данного метода, а также результаты качественного анализа позволяют проводить комплексную оценку рисков финансово-хозяйственной деятельности предприятий. Количественная оценка рисков проводится на основе данных, полученных при качественной их оценке, то есть оцениваться будут только те риски, которые ...
... своей деятельности банки сталкиваются с множеством рисков, успех управления которыми зависит от уровня оценки вероятности их наступления, а также выбора метода их минимизации. 1.2. Роль управления банковскими рисками в современных условиях Банк по своему определению должен являться одним из наиболее надежных институтов общества, представляет основу стабильности экономической системы. При ...
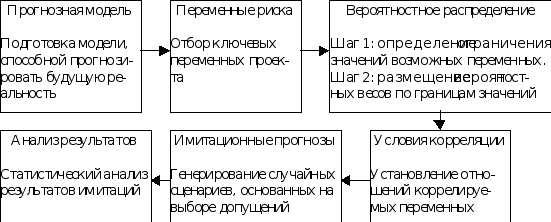
... по методу «Монте-Карло», так же находится выше прямых NPV и графика чувствительности при 3% снижении объема поступлений. Заключение Теоретическое рассмотрение методов оценки рисков инвестиционного проекта на примере проекта строительства нового хранилища нефтепродуктов ООО «Концепт» приводит к следующим выводам: целями и задачами проведения оценки инвестиционного проекта является определение ...
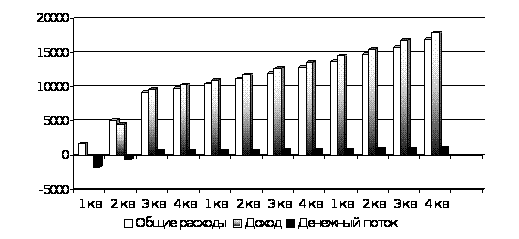
0 комментариев