Навигация
Диверсификация финансовых активов. Рыночный и собственный риск портфеля
14. Диверсификация финансовых активов. Рыночный и собственный риск портфеля
Исходя из рыночной модели, общий риск финансового актива (σi2) состоит из двух частей:
- рыночный или систематический риск;
- собственный или несистемный риск.
![]() ,
,
где σi2 – общий риск финансового актива;
βiI2 σI2 – рыночный риск;
σεi2 – собственный риск.
Мерой собственного риска является дисперсия случайной погрешности.
Общий риск портфеля
Рассмотрим случай, когда доходность каждого рискового финансового актива из портфеля связана с доходностью рыночного индекса.
Доходность портфеля может быть определена как:
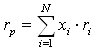 ,
,
где хi – доля средств, вложенных в актив i;
N – количество финансовых активов.
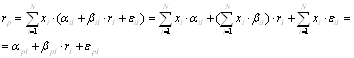
![]() - рыночная модель портфеля финансовых активов.
- рыночная модель портфеля финансовых активов.
![]()
![]()
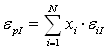
Данная модель является прямым обобщением рыночных моделей отдельных финансовых активов, входящих в его состав.
Общий риск портфеля измеряется дисперсией его доходности и обозначается σр2:
![]()
Он состоит из рыночного и собственного риска.
Увеличение диверсификации может привести к снижению общего риска портфеля. Это происходит вследствие сокращения собственного риска портфеля. В то время как рыночный риск портфеля остается примерно таким же.
Чем более диверсифицирован портфель, тем меньше каждая доля актива в нем. При этом значение βpI не меняется существенным образом, за исключением случаев преднамеренного включения в портфель финансовых активов с относительно низким или высоким значением βiI.
Поэтому диверсификация приводит только к усреднению среднего риска.
Иная ситуация при рассмотрении риска портфеля
Предположим, что во все финансовые активы инвестировано одинаковое количество средств, т.е. доля xi каждого финансового актива равна 1/N.
![]() (средний собственный риск).
(средний собственный риск).
Собственный риск портфеля в N-раз меньше среднего собственного риска финансового актива.
Более диверсифицированный портфель – средний собственный риск практически не изменится.
Пример:
Первый портфель ценных бумаг состоит из 4-х ценных бумаг, второй – из 10. Все ценные бумаги имеют β = 1 и собственный риск = 30%. В обоих портфелях доля всех ценных бумаг одинакова. Вычислить общий риск каждого портфеля, если стандартное отклонение индекса рынка составляет 20%.
![]()
![]()
![]()
![]()
15. Оценка рисков безрисковых активов
Безрисковый актив предполагает, что доход по нему является определенным в конце инвестиционного периода.
Стандартное отклонение для безрискового актива рано нулю.
Ковариация между ставкой доходности по безрисковому активу и ставкой доходности по рисковому активу также равна нулю.
Т.е. безрисковые актив имеет фиксированный доход и нулевую вероятность неуплаты (государственные ценные бумаги).
При этом срок погашения совпадает с периодом владения, т.е. отсутствует неопределенность.
Такое инвестирование называется безрисковым кредитованием.
Появление новых возможностей при инвестировании существенно расширяет достижимое множество портфеля активов и изменяет расположение эффективного множества.
Рассмотрим ожидаемую доходность и стандартное отклонение для портфеля, состоящего из инвестиций в безрисковые активы в сочетании с одним рисковым активом.
Пример:
A, B, C + 1 безрисковый актив
х1 – доля актива
х4 = 1 – х1 – доля в безрисковом активе
| Портфели | х1 | х4 | rp | σp |
| A | 0,00 | 1,00 | 4% | 0,0 |
| B | 0,25 | 0,75 | 7,05% | 3,02 |
| C | 0,5 | 0,5 | 10,10% | 6,04 |
| D | 0,75 | 0,25 | 13,15% | 9,06 |
Предположим, что х4 имеет ставку доходности 4%.
r4 = 4%
r1 = 16,2%
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Любой портфель, состоящий из комбинации безрисковых и рисковых активов, будут иметь ожидаемую доходность и стандартное отклонение, которые лежат на одной прямой, соединяющей точки, соответствующие этим активам.
Одновременное инвестирование в безрисковые активы и рисковый портфель
Рассмотрим, что произойдет, когда портфель, состоящий их активов А и С (0,8 и 0,2 соответственно) - рисковый портфель объединен с безрисковыми активами.
![]()
![]()
rpи σр для рискового портфеля и безрисковых активов могут быть рассчитаны аналогичным путем.
![]()
![]()
Рассмотрим инвестиции в портфель, состоящий из портфеля А и С и безрисковых активов.
xpAC = 0,25
х4 = 0,75
![]()
![]()
Объединение безрисковых активов с рисковым портфелем может рассматриваться точно также как и объединение безрисковых активов с рисковыми активами.
В обоих случая их доходности и стандартное отклонение лежат на прямой линии, соединяющей крайние точки.
16. Влияние безрискового кредитования на эффективное множество
Для безрисковых активов А, В и С.
хА = 0,12
хВ = 0,19
хС = 0,69
rpт = 22,4%
σрт = 15,2%
Особенности портфеля Т:
1. Из существующего портфеля, состоящих из этих активов, который будучи соединен прямой линией с точкой, соответствующей безрисковому активу, лежал бы выше и левее данного портфеля, т.е. это наиболее оптимальный портфель.
2. Первое условие важно, потом что часть эффективного множества в модели Марковца отсекается этой линией.
Теперь эффективное множество состоит из прямой линии и искривленного отрезка.
17. Учет возможностей безрискового заимствования
Если рассматривать возможность заимствования, то инвестор:
- не ограничен начальным капиталом;
- платит проценты по займам.
Если ставка процентов и известная и неопределенность отсутствует, то можно говорить о безрисковом заимствовании.
Предполагается, что процентная ставка по займам равна ставке, которая может быть заработана инвестором при инвестировании в безрисковые активы.
В данном случае безрисковая ставка равна процентам по займам (4%).
Если мы говорим о безрисковом кредитовании, то доля х4 положительная (х4 > 0).
Если же мы говорим о безрисковом заимствовании, то доля х4 отрицательная (x4 < 0).
Пример:
10 000$ инвестируем в хрАС = 1
12 500$ - вкладываем, 2 500$ - заимствование
х4 = - 0,25
хрАС = 1,25 + (-0,25) = 1
хрАС = 1,25
Лучи означают возможность одновременного использования и безрискового кредитования, и безрискового заимствования.
Если используется безрисковое заимствование, то точки расп-ся.
Похожие работы
... и на транспортные услуги и т.п. Внутренние факторы связаны с ошибками и упущениями руководства и персонала, с их готовностью к выбору рисковой стратегии в деятельности предприятия. 2. Статистические методы оценки риска Известны два вида анализа рисков: качественный и количественный. Качественный анализ дает возможность определить факторы и потенциальные области риска, выявить его виды. ...
... а именно: оценку рисков по контрольным точкам финансово-хозяйственной деятельности. Использование данного метода, а также результаты качественного анализа позволяют проводить комплексную оценку рисков финансово-хозяйственной деятельности предприятий. Количественная оценка рисков проводится на основе данных, полученных при качественной их оценке, то есть оцениваться будут только те риски, которые ...
... своей деятельности банки сталкиваются с множеством рисков, успех управления которыми зависит от уровня оценки вероятности их наступления, а также выбора метода их минимизации. 1.2. Роль управления банковскими рисками в современных условиях Банк по своему определению должен являться одним из наиболее надежных институтов общества, представляет основу стабильности экономической системы. При ...
... по методу «Монте-Карло», так же находится выше прямых NPV и графика чувствительности при 3% снижении объема поступлений. Заключение Теоретическое рассмотрение методов оценки рисков инвестиционного проекта на примере проекта строительства нового хранилища нефтепродуктов ООО «Концепт» приводит к следующим выводам: целями и задачами проведения оценки инвестиционного проекта является определение ...



0 комментариев