Навигация
Умножение векторов и матриц
21092
знака
0
таблиц
9
изображений
2. Умножение векторов и матриц
Среди n-мерных векторов и векторных операций над ними важно выделить сумму n векторов, умноженных на числовые константы:
,
которая при произвольном выборе 
в частности может оказаться нулевым вектором (с нулевыми компонентами) или одним из суммируемых векторов 
. Если нулевой вектор при суммировании не нулевых векторов можно получить лишь в случае, когда все 
, то такие векторы в наборе называют линейно независимыми. Такими векторами в частности будут единичные векторы 
, у которых все компоненты нулевые, кроме единичной компоненты, расположенной на j-строке.
Линейно независимый набор единичных векторов с геометрической точки зрения можно рассматривать как n-мерную систему координат. Набор компонент любого вектора в этой n-мерной системе определяет координаты точки конца вектора, исходящего из начала координат, а также являются длинами проекций вектора на координатных осях.
Среди матриц размера 
и операций с ними в первую очередь необходимо отметить операцию умножения матрицы на матрицу. Необходимость введения операции умножения матриц возникает уже при первом взгляде на полученную векторную форму записи линейного уравнения 
. Векторы слева и справа имеют равные компоненты. Так как коэффициенты в строках матрицы в общем произвольны по величине, то соответствующие компоненты вектора x не обязаны быть равными компонентам вектора y. Последнее означает, что умножение вектора x на матрицу A вызвало изменение длины и направления вектора x. Если аналогичное преобразование выполняется над вектором правой части до решения уравнения, то вектор левой части должен быть преобразован так же:
.
Фактически мы имеем дело с заменой системы координат. Рассмотрим методику вычисления коэффициентов результирующей матрицы уравнения:
,
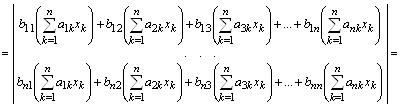
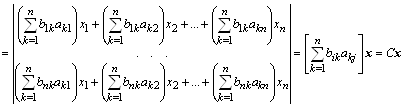где 
– элемент матрицы С, равный скалярному произведению вектор-строки 
матрицы В на вектор-столбец 
матрицы А.
Произведение матриц в общем случае не коммутативно. Ассоциативный и распределительный законы в матричных выражениях выполняются.
3. Нормы векторов и матриц
Интерпретация упорядоченного набора чисел, как вектора в многомерном пространстве, позволяет говорить и о его длине. В прямоугольной системе координат по известным длинам проекций на координатные оси длину самого вектора вычисляют, как корень квадратный из суммы квадратов проекций:
,
где – компоненты вектора 
,
– евклидова норма вектора, его длина.
В качестве нормы в литературе иногда используют квадрат длины вектора или другое выражение с компонентами вектора, лишь бы оно обладало свойствами расстояния: было положительным, линейным и удовлетворяло неравенству треугольника.
Деление вектора на величину его нормы называют нормированием, т.е. приведением вектора к единичной длине.
Норма матрицы в принципе тоже может быть определена в виде корня квадратного из суммы квадратов ее элементов или другими выражениями со свойствами расстояний. Однако в ряде случаев работы с векторно-матричными выражениями нормы векторов и матриц должны быть согласованными ввиду того, что результатом произведения матрицы на вектор является опять же вектор. Если выражение для нормы вектора принято, то
,
где функция sup говорит о том, что из всех отношений норм, стоящих в числителе и знаменателе, взятых при любом векторе x, кроме нулевого, выбирается наименьшее, т.е. это функция выбора нижней границы значений. Согласованная матричная норма для евклидовой нормы вектора удовлетворяет неравенству
.
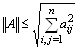Нормы вектора и матрицы служат, в основном, для сопоставительной оценки матриц и векторов, указывая на возможный диапазон представления строгих числовых характеристик. К числу последних, в первую очередь, нужно отнести определители матриц, собственные значения и собственные векторы матриц и ряд других.
Похожие работы
в первом столбце. Матрице соответствует множество решений системы линейных уравнений Ответ: получили решение: Задача 2 Даны координаты вершин треугольника АВС Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и ВС и их угловые коэффициенты; 3) внутренний угол при вершине В в радианах с точностью до 0,01 4) уравнение медианы АЕ; 5) уравнение и длину высоты CD; 6) ...
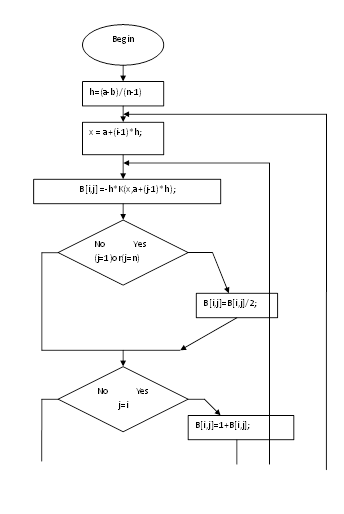
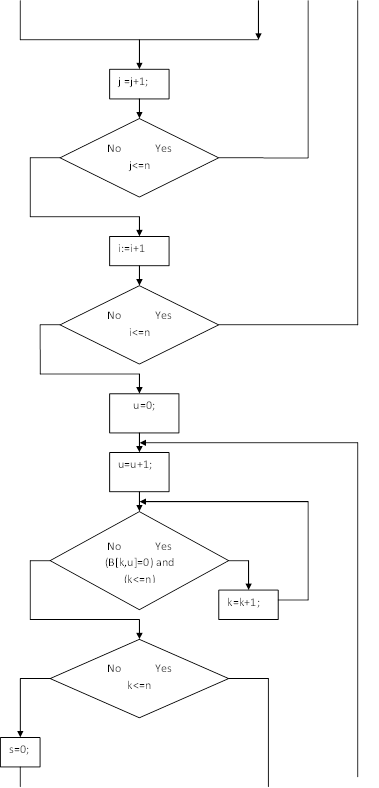
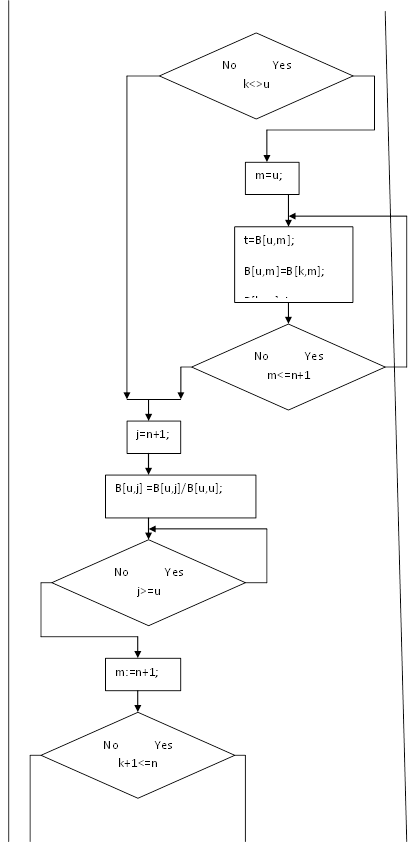
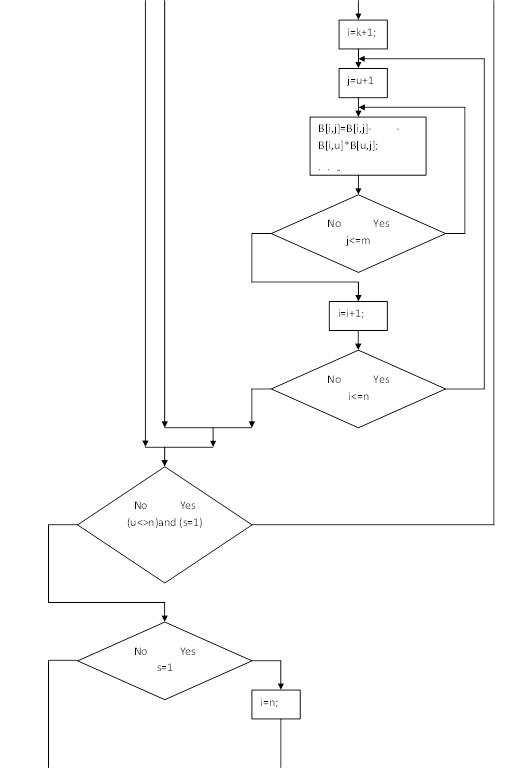
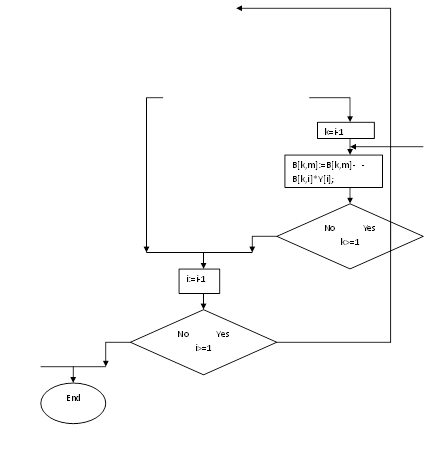
... решение линейного интегрального уравнения составим алгоритм. Представим алгоритм в виде блок-схемы. y[i]=B[i,m]; Используя данную блок-схему, напишем соответствующую функцию. Функция решения линейных интегральных уравнений будет реализована на С++. bool solvefredholm2(const double& a, const double& b, const int& n, ap::real_1d_array& y, ...
... шаг интегрирования ; tp – время интегрирования трех точечным методом прогноза и коррекции , ta – время интегрирования по методу Адамса-Башфорта , NU – массив начальных условий . Данная процедура способна производить решения систем линейных дифференциальных уравнений произвольного размера , на произвольном промежутке времени интегрирования . Вычисленные данные записываются в файлы prandcom*.df . ...
... понятия собственного числа линейного оператора А. 120. Определите, каким является базис а=(1/, 1/,1/), b=(1/, -1/, 0), с =(1/, 1/,-2/). Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету ЛИНЕЙНАЯ АЛГЕБРА Билет № 26 121. Приведение матрицы к ступенчатому виду методом Гаусса. Пример. 122. ...
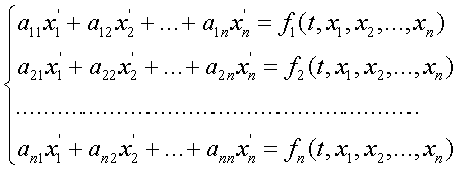
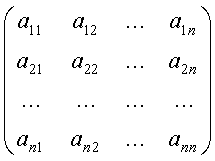
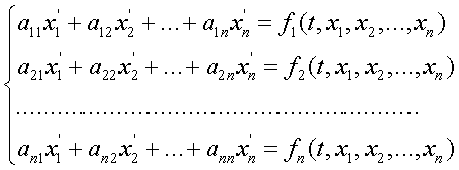
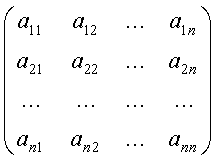
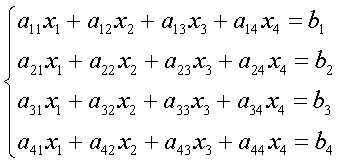
0 комментариев