Навигация
Ортогональные матрицы из собственных векторов
21092
знака
0
таблиц
9
изображений
6. Ортогональные матрицы из собственных векторов
Из правых собственных векторов можно составить матрицу T, а из левых – матрицу 
, которые обладают уникальными свойствами по отношению к матрице A.
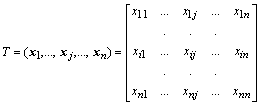
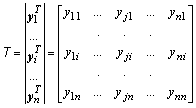
Умножив матрицу A слева на матрицу , а справа – на матрицу T, после несложных преобразований получим:
.
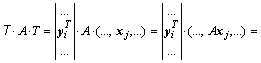
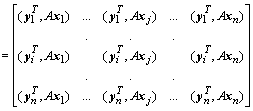Каждое скалярное произведение 
в матрице, принимая во внимание линейную независимость собственных векторов, полученных для различных собственных значений, можно преобразовать так:
Поэтому, результатом преобразования матрицы A будет диагональная матрица с собственными значениями, расположенными на диагонали:
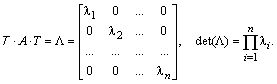
Если вместо A взять единичную матрицу и проделать аналогичные преобразования, то станет очевидным равенство 
, откуда следует 
. Последнее позволяет для преобразования матрицы A в диагональную обходиться только системой правых собственных векторов-столбцов:
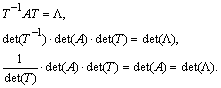
Последнее показывает, что умножение матрицы A на 
слева и на S справа, где S – произвольная не особая матрица, преобразует ее в некоторую матрицу B, которая имеет определитель, равный определителю матрицы A. Такие преобразования матриц называют эквивалентными (подобными).
Продолжая использовать T-матрицу, несложно получить следующие важные результаты:
.
7. Функции с матричным аргументом
Пусть теперь задана некоторая матричная функция от матрицы A:
.
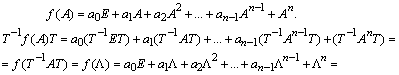
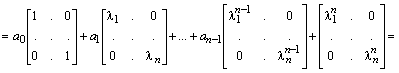
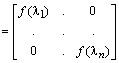С другой стороны очевидно и обратное
,
где 
– матрица с одной единицей на i-том месте диагонали (
).
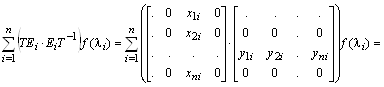
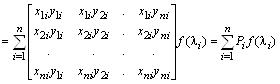
где 
– проекторы матрицы A, образуемые умножением одноименных правых и левых собственных векторов по правилам умножения прямоугольных матриц с размерами соответственно 
и 
. Сумма проекторов 
.
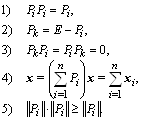
Проекторы обладают свойствами идемпотентных матриц, т.е. матриц, все степени которых равны первой. Для невырожденных проекторов (
) матрицы A (
) справедливо:
Представление функции от матрицы A в виде взвешенной суммы проекций называется спектральным разложением матричной функции по собственным значениям матрицы A:
.
Если в качестве матричных функций взять 
и 
, то их спектральные разложения будут следующими:
Похожие работы
в первом столбце. Матрице соответствует множество решений системы линейных уравнений Ответ: получили решение: Задача 2 Даны координаты вершин треугольника АВС Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и ВС и их угловые коэффициенты; 3) внутренний угол при вершине В в радианах с точностью до 0,01 4) уравнение медианы АЕ; 5) уравнение и длину высоты CD; 6) ...
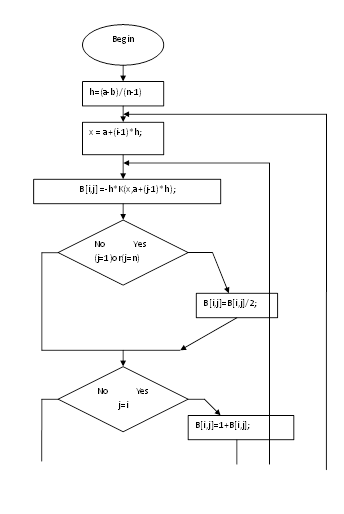
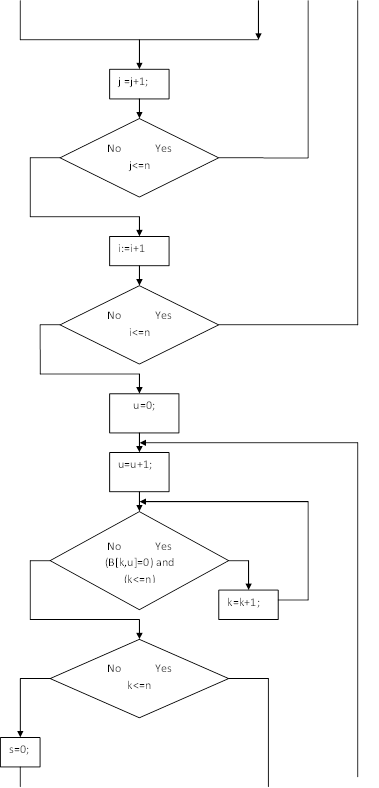
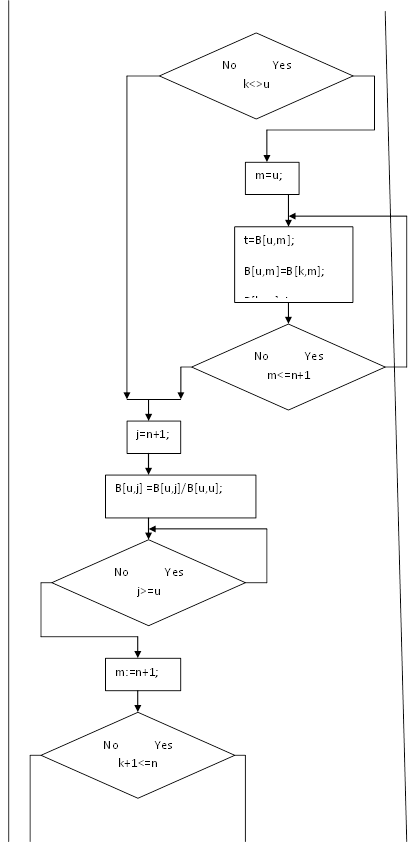
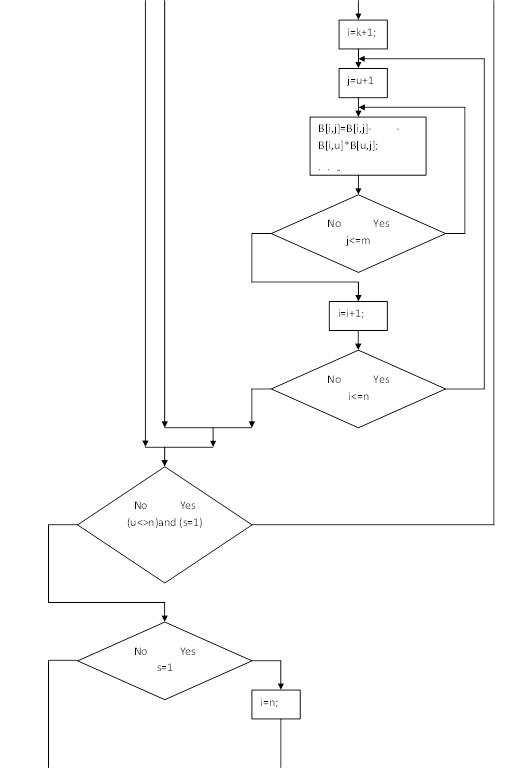
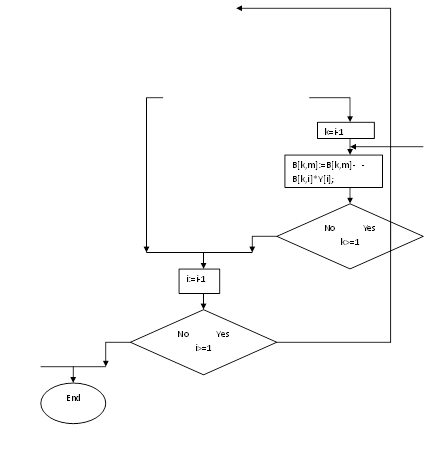
... решение линейного интегрального уравнения составим алгоритм. Представим алгоритм в виде блок-схемы. y[i]=B[i,m]; Используя данную блок-схему, напишем соответствующую функцию. Функция решения линейных интегральных уравнений будет реализована на С++. bool solvefredholm2(const double& a, const double& b, const int& n, ap::real_1d_array& y, ...
... шаг интегрирования ; tp – время интегрирования трех точечным методом прогноза и коррекции , ta – время интегрирования по методу Адамса-Башфорта , NU – массив начальных условий . Данная процедура способна производить решения систем линейных дифференциальных уравнений произвольного размера , на произвольном промежутке времени интегрирования . Вычисленные данные записываются в файлы prandcom*.df . ...
... понятия собственного числа линейного оператора А. 120. Определите, каким является базис а=(1/, 1/,1/), b=(1/, -1/, 0), с =(1/, 1/,-2/). Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету ЛИНЕЙНАЯ АЛГЕБРА Билет № 26 121. Приведение матрицы к ступенчатому виду методом Гаусса. Пример. 122. ...
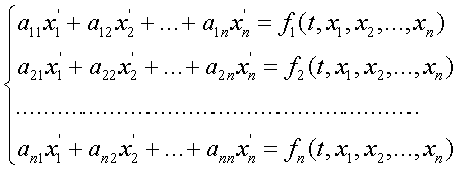
0 комментариев