Навигация
Вычисление проекторов матрицы
21092
знака
0
таблиц
9
изображений
8. Вычисление проекторов матрицы
Проекторы матрицы можно также вычислить, воспользовавшись интерполяционным многочленом Лагранжа с матричным аргументом:
По известному спектру 
проекторы матрицы можно найти и методом неопределенных коэффициентов. Для чего выбирают такие функции от матрицы A, которые вычисляются очевидным образом, например, такие:
Записывая разложение для каждой функции, получим следующую систему линейных уравнений относительно проекторов:
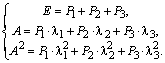
В случае, когда в спектре матрицы имеются кратные собственные значения, вычисление проекторов осуществляется по интерполяционным формулам Лагранжа, учитывающим еще и заданные значения производных в отдельных точках. Разложение матричной функции по значениям ее на спектре в этом случае имеет вид:
где 
– значения i-тых произ-водных функции в точках, соответствующих различным (не кратным) корням характеристического многочлена,
– число кратных корней 
,
– проекторы кратных корней, в выражении которых содержатся
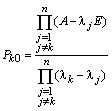– проекторы различных корней.
9. Пример использования числовых характеристик матриц
Знание собственных значений матрицы и ее проекторов позволяет выполнять вычисления аналитических функций получающихся, например, при решениях систем линейных дифференциальных уравнений, при исследованиях эквивалентных матричных преобразований и пр.
Для примера построим матрицу с заданными собственными значениями 
и собственными векторами, основанными на векторах 
.
Сначала необходимо убедиться в линейной независимости исходных векторов и добиться того, чтобы левые и правые одноименные собственные векторы оказались ортогональными, т.е. 
. Проверка линейной независимости может быть объединена с процессом ортогонализации заданной системы векторов методом Грама-Шмидта.
Для заданных векторов построим систему векторов 
таких, что 
, следующим образом:
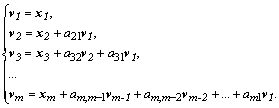
Откуда последовательно находятся коэффициенты 
:
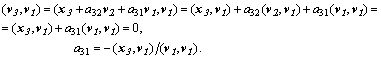
Взаимной ортогональности векторов v можно было бы добиваться и так, чтобы каждый 
был ортогонален каждому 
, положив 
и приравняв нулю скалярные произведения 
:
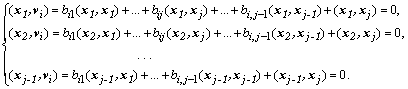
Определитель этой системы называют определителем Грама:
,
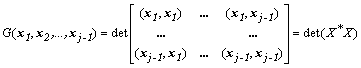где 
- матрица, в общем случае комплексно сопряженная с матрицей
, составленной из заданных векторов.
Если грамиан положителен, а он всегда неотрицателен, то векторы 
линейно независимы, а если равен нулю, то зависимы. Это один из способов проверки конкретного набора векторов на их линейную независимость.
Для заданного выше набора векторов определитель произведения матрицы X на транспонированную X* будет равен
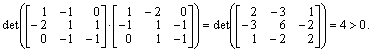
Таким образом, заданная система векторов линейно независима. Для построения ортонормированной системы векторов последовательно вычислим коэффициенты и ортогональные векторы:
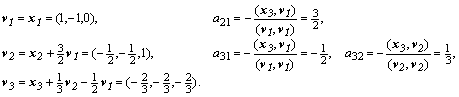
После нормирования векторы образуют правую систему собственных векторов. Транспонированная Т-матрица с этими векторами есть 
-матрица (
); ее строки являются собственными левосторонними векторами:
.
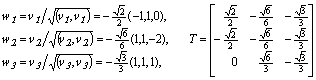Внешнее (матричное) произведение каждого нормированного вектора 
самого на себя дает нам проекторы искомой матрицы:
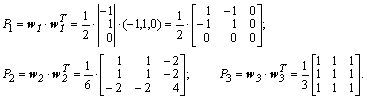
Умножая каждое собственное значение 
из заданного набора на свой проектор и суммируя, получим:
.
Аналогично получается обратная матрица:
.
С помощью этих же проекторов вычисляется любая аналитическая функция, аргументом которой является матрица A:
.
Похожие работы
в первом столбце. Матрице соответствует множество решений системы линейных уравнений Ответ: получили решение: Задача 2 Даны координаты вершин треугольника АВС Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и ВС и их угловые коэффициенты; 3) внутренний угол при вершине В в радианах с точностью до 0,01 4) уравнение медианы АЕ; 5) уравнение и длину высоты CD; 6) ...
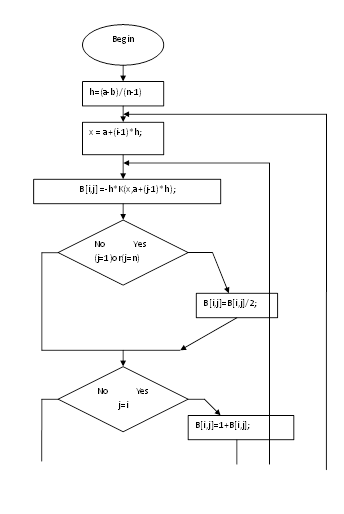
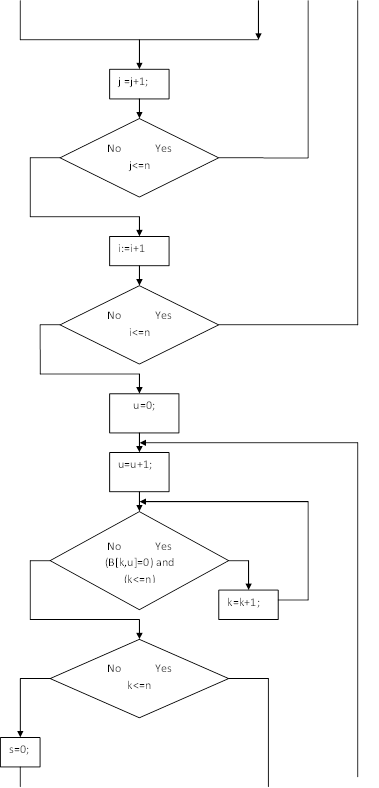
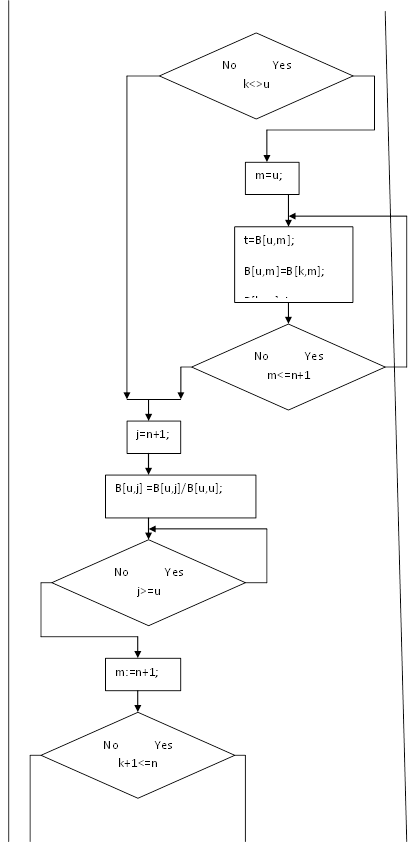
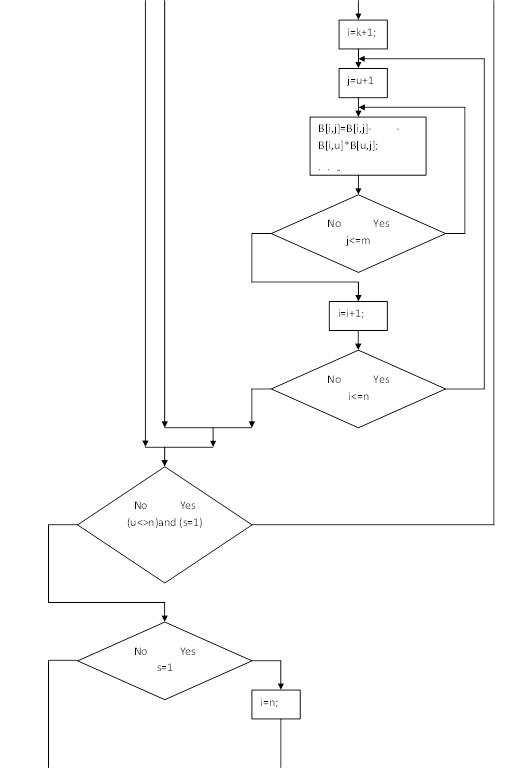
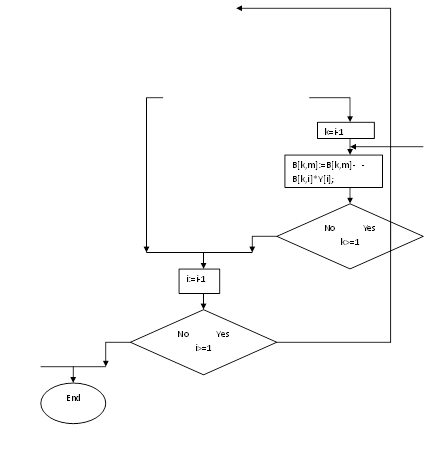
... решение линейного интегрального уравнения составим алгоритм. Представим алгоритм в виде блок-схемы. y[i]=B[i,m]; Используя данную блок-схему, напишем соответствующую функцию. Функция решения линейных интегральных уравнений будет реализована на С++. bool solvefredholm2(const double& a, const double& b, const int& n, ap::real_1d_array& y, ...
... шаг интегрирования ; tp – время интегрирования трех точечным методом прогноза и коррекции , ta – время интегрирования по методу Адамса-Башфорта , NU – массив начальных условий . Данная процедура способна производить решения систем линейных дифференциальных уравнений произвольного размера , на произвольном промежутке времени интегрирования . Вычисленные данные записываются в файлы prandcom*.df . ...
... понятия собственного числа линейного оператора А. 120. Определите, каким является базис а=(1/, 1/,1/), b=(1/, -1/, 0), с =(1/, 1/,-2/). Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету ЛИНЕЙНАЯ АЛГЕБРА Билет № 26 121. Приведение матрицы к ступенчатому виду методом Гаусса. Пример. 122. ...
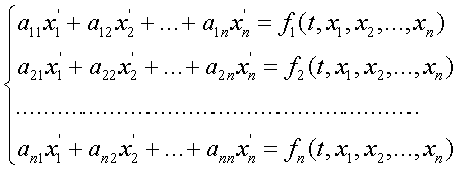
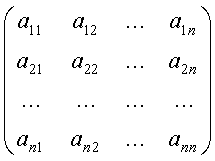
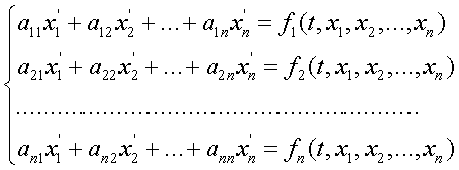
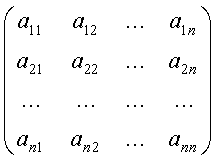
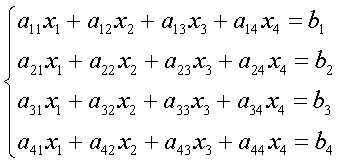
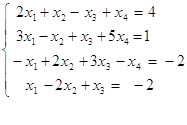
0 комментариев