Навигация
1.2 Основні теореми
Теорема 1 (про диференційовність композиції відображень). Нехай ![]() – лінійні нормовані простори й задані відображення
– лінійні нормовані простори й задані відображення ![]() , де
, де ![]() ,
, ![]() – відкрита множина;
– відкрита множина; ![]() , де
, де ![]() ,
, ![]() – відкрита множина. Якщо множина
– відкрита множина. Якщо множина ![]() не порожня , відображення
не порожня , відображення ![]() диференційовне в точці
диференційовне в точці ![]() , а
, а ![]() диференційовне в точці
диференційовне в точці ![]() , то складне відображення
, то складне відображення ![]() диференційовне в точці
диференційовне в точці ![]() і
і
![]() .
.
Доведення. Насамперед, якщо ![]() достатньо мале, то в силу відкритості множин
достатньо мале, то в силу відкритості множин ![]() та
та ![]() й неперервності відображень
й неперервності відображень ![]() і
і ![]() відповідно в точках
відповідно в точках ![]() та
та ![]() , точки
, точки ![]() і
і ![]() не вийдуть за границі множин
не вийдуть за границі множин ![]() та
та ![]() . Далі маємо
. Далі маємо
![]() .
.
Оскільки ![]() диференційовне в точці
диференційовне в точці ![]() , то
, то
![]() ,
,
де ![]() , якщо
, якщо ![]() . В свою чергу,
. В свою чергу,
![]()
де ![]() , якщо
, якщо ![]() . Тому
. Тому
![]()
Вираз ![]() є лінійним оператором по
є лінійним оператором по ![]() , і залишається довести, що
, і залишається довести, що ![]() , якщо
, якщо ![]() .
.
Маємо
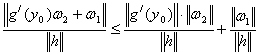 .
.
Перший доданок справа прямує до нуля, оскільки ![]() , якщо
, якщо ![]() . Прямування до нуля другого доданка можна довести так. Оскільки
. Прямування до нуля другого доданка можна довести так. Оскільки ![]() диференційовне в точці
диференційовне в точці ![]() , то
, то ![]() , якщо
, якщо ![]() . Тому для будь-якого
. Тому для будь-якого ![]() знайдеться
знайдеться ![]() , таке, що
, таке, що ![]() , якщо
, якщо ![]() . В свою чергу, в силу неперервності
. В свою чергу, в силу неперервності ![]() в точці
в точці ![]() для даного
для даного ![]() знайдеться
знайдеться ![]() таке, що
таке, що ![]() , якщо
, якщо ![]() . Далі, оскільки
. Далі, оскільки ![]() диференційовне в точці
диференційовне в точці ![]() , то знайдеться
, то знайдеться ![]() таке, що
таке, що 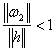 , якщо
, якщо ![]() . Нехай
. Нехай ![]() . При
. При ![]() маємо
маємо
![]() ,
,
і оскільки ![]() довільне, то це означає, що
довільне, то це означає, що ![]() , якщо
, якщо ![]() .
.
Теорему доведено.
Приклад 5. Розглянемо відображення ![]() , диференційоване на відкритій множині
, диференційоване на відкритій множині ![]() , і точки
, і точки ![]() такі, що
такі, що ![]() . Тоді функція
. Тоді функція ![]() , визначена рівністю
, визначена рівністю
![]() ,
,
диференційовна на ![]() і
і ![]() .
.
Приклад 6. Нехай відображення ![]() диференційоване на
диференційоване на ![]() і
і ![]() – лінійний неперервний оператор. Тоді
– лінійний неперервний оператор. Тоді ![]() – відображення, диференційовне на
– відображення, диференційовне на ![]() , і
, і ![]() .
.
Наступна теорема є аналогом теореми Лагранжа про скінченні прирости дійсних функцій дійсних аргументів.
Теорема 2 (про скінченні прирости). Нехай відображення ![]() диференційовне на
диференційовне на ![]() і відрізок
і відрізок ![]() цілком входить до
цілком входить до ![]() . Тоді
. Тоді
![]() .
.
Доведення. Розглянемо відображення ![]() , де
, де ![]() . Це відображення неперервне на
. Це відображення неперервне на ![]() як композиція неперервних відображень
як композиція неперервних відображень ![]() та
та ![]() , і в силу теореми 1 диференційовне всередині
, і в силу теореми 1 диференційовне всередині ![]() , при цьому
, при цьому
![]() .
.
Тому для будь-якого лінійного функціоналу ![]() дійсна функція
дійсна функція ![]() дійсного аргументу
дійсного аргументу ![]() неперервна на
неперервна на ![]() і диференційовна принаймні всередині
і диференційовна принаймні всередині ![]() . Тобто, за теоремою Лагранжа
. Тобто, за теоремою Лагранжа
![]() . (5)
. (5)
Але ![]() і
і
![]() .
.
Тому рівність (5) набуває вигляду
![]() .
.
Нехай ![]() – функціонал з нормою, що дорівнює одиниці, і такий, що
– функціонал з нормою, що дорівнює одиниці, і такий, що ![]() . Тому
. Тому
![]() .
.
Теорему доведено.
Похожие работы
... Чарка, стакан 4 320 2 80 400 Столові прибори (комплект) 4 320 2 80 400 Далі наведемо характеристику посуду, який будуть використовувати в комплексному закладі ресторанного господарства (табл. 2.8–2.11). Таблиця 2.8. Характеристика та призначення класичного вітчизняного порцелянового та фаянсового посуду Найменування Розміри, мм Місткість, см3, порцій Призначення ...
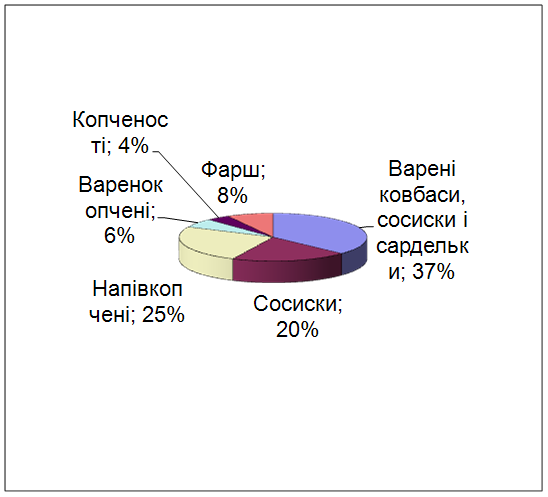
... ється, окремими технологічними операціями, специфічними виглядом і смаком, енергетичною цінністю та іншими ознаками. Варені ковбаси займають 53-60% в загальному виробництві ковбасних виробів. 3.1 Характеристика підприємства Ковбасний цех спільного підприємства Сумський виробничий комбінат розміщєно напівнічному-сході м. Суми, на відстані 1000 м від житлових кварталів. Окрім ковбасного цуху ...
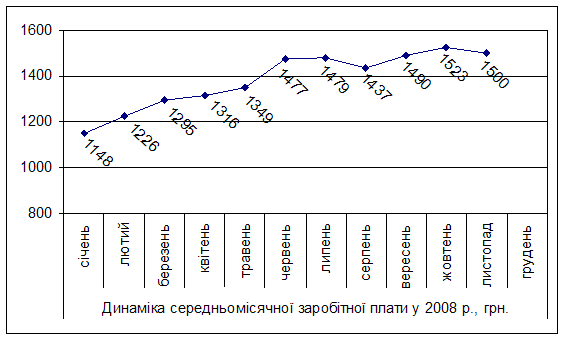
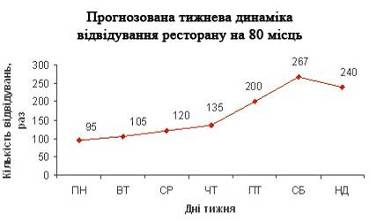
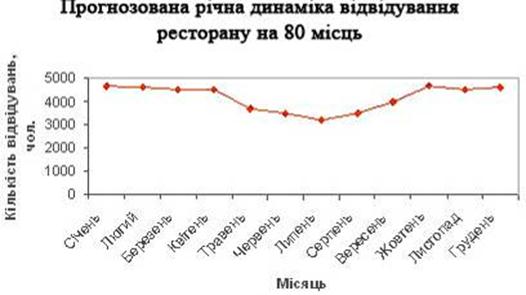
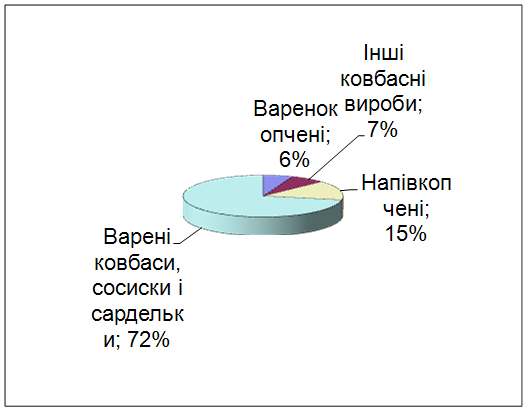
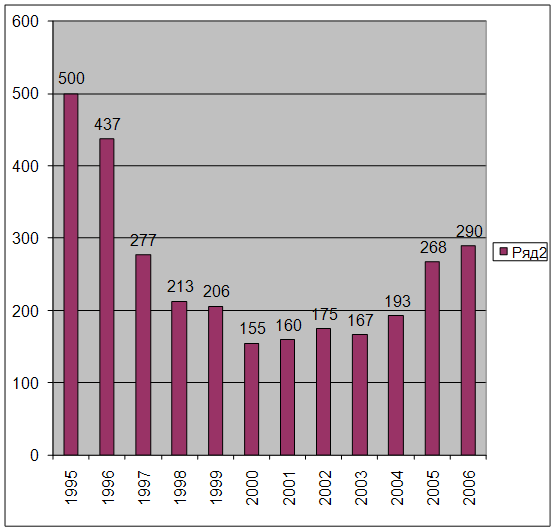
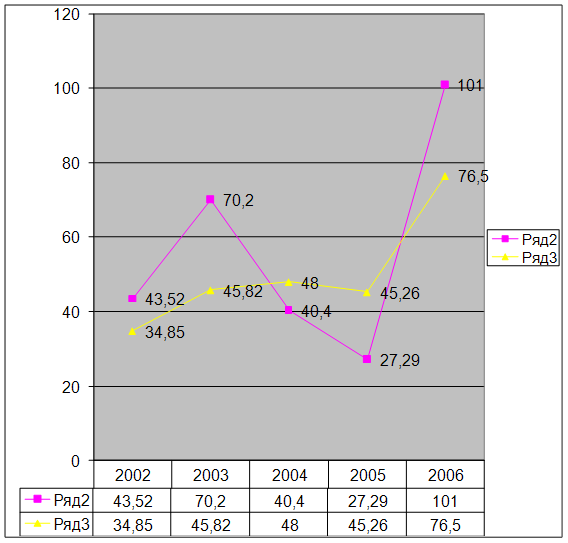
0 комментариев