Навигация
Довести, що похідна Фреше диференційовного в точці відображення визначається єдиним чином
1. Довести, що похідна Фреше диференційовного в точці відображення визначається єдиним чином.
Доведення
Нехай ![]() ,
, ![]() – дві похідні Фреше в точці x, тоді
– дві похідні Фреше в точці x, тоді
![]() , де
, де 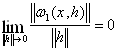 (1)
(1)
![]() , де
, де 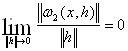 (2)
(2)
Розглянемо різницю (2)-(1):
![]()
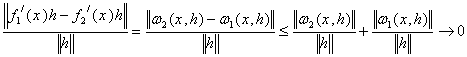 , якщо
, якщо ![]()
Це прямування до нуля нетривіально, тобто
![]()
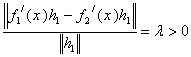
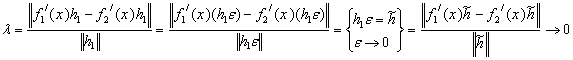
якщо ![]() .
.
Тобто, похідна Фреше диференційованого відображення визначається єдиним чином.
2. Довести, що якщо оператор f диференційовний за Фреше в точці x, то f неперервний в цій точці.
Доведення
![]() Якщо
Якщо ![]() та
та 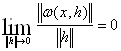 , то
, то ![]() .
.
3. Довести, що якщо ![]() , то
, то ![]() (нульовий оператор).
(нульовий оператор).
Доведення.
Нехай оператор ![]() диференційовний за Фреше, тобто
диференційовний за Фреше, тобто
![]() , де
, де 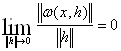
Нехай ![]() , тоді
, тоді ![]() (
(![]() – нульовий оператор)
– нульовий оператор)
![]() , звідки
, звідки ![]() (нульовий оператор, який діє на h).
(нульовий оператор, який діє на h).
4. Довести, що похідною Фреше лінійного неперервного відображення є саме це відображення.
Доведення.
Нехай оператор ![]() диференційований за Фреше, тобто
диференційований за Фреше, тобто
![]() , де
, де 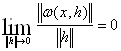 .
.
![]()
![]() – лінійний неперервний оператор
– лінійний неперервний оператор
5. Нехай f, g – два неперервних відображення з X в Y. Довести, що якщо f та g диференційовні за Фреше в точці x, то відображення f+g та cf, де c-const, також диференційовні в цій точці, причому
![]() ,
, ![]()
Доведення.
Розглянемо
![]()
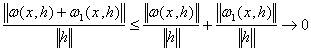 , якщо
, якщо ![]() .
.
Тепер
![]()
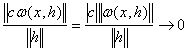 ,
,
якщо ![]() .
.
6. Нехай ![]() , де
, де ![]() – дійсний гільбертів простір. Знайти похідну Фреше в точці x.
– дійсний гільбертів простір. Знайти похідну Фреше в точці x.
Розв’язок.
![]()
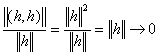
Тобто, ![]() .
.
7. Знайти похідну Фреше функціонала ![]() в точці x дійсного гільбертова простору.
в точці x дійсного гільбертова простору.
Розв’язок
Нехай ![]() ,
, ![]() . Тоді
. Тоді ![]() .
.
Розглянемо ![]() ,
, ![]() . Тоді
. Тоді
![]()
Тепер
![]() , де
, де ![]() .
.
Тоді
![]() , де
, де ![]() .
.
8. Знайти похідну Фреше відображення 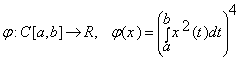 .
.
Розв’язок
Нехай
![]() ,
, 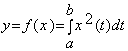 .
.
Тоді
![]() .
.
Розглянемо ![]() ,
, ![]() . Тоді
. Тоді
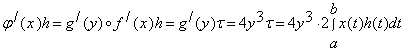
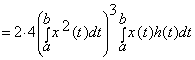 , де
, де ![]() .
.
9. Знайти похідну Фреше відображення ![]() .
.
Розв’язок
Нехай
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Тоді
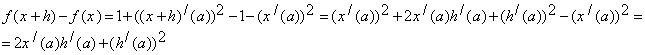
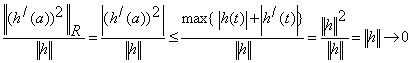
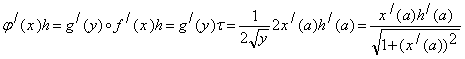 .
.
10. Знайти похідну Фреше відображення ![]() .
.
Розв’язок
Нехай ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Тоді
. Тоді
![]() ,
, ![]() .
.
11. Знайти похідну Фреше відображення 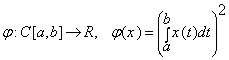 .
.
Розв’язок
Нехай ![]() ,
, 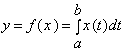 ,
,![]() ,
, ![]() . Тоді
. Тоді
![]()
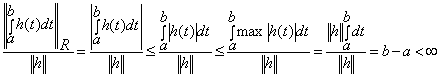
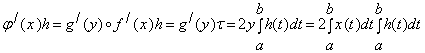 .
.
12. Задано відображення ![]() . Довести, що
. Довести, що ![]() .
.
Доведення
Розглянемо для ![]()
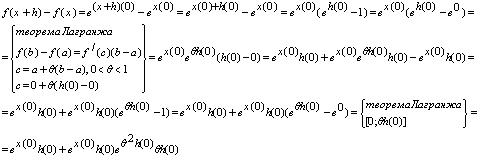
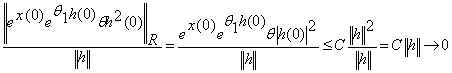 , якщо
, якщо ![]()
![]()
Лінійність:
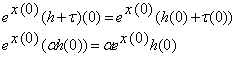
Обмеженість:
![]()
Остаточно маємо ![]() .
.
13. Задано відображення ![]() . Довести, що
. Довести, що ![]() .
.
Доведення
Розглянемо для ![]()
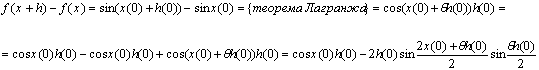
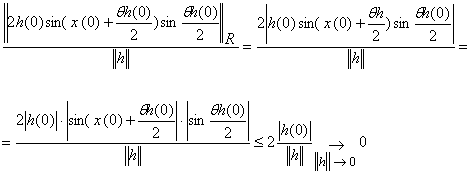
Остаточно маємо ![]() .
.
14. Задано відображення ![]() . Довести, що
. Довести, що ![]() .
.
Доведення
Розглянемо для ![]()
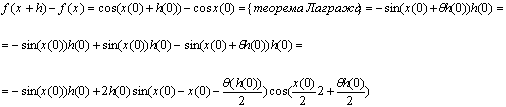
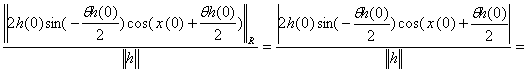
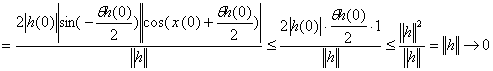
Остаточно маємо ![]() .
.
15. Знайти похідну Фреше відображення ![]() .
.
Розв’язок
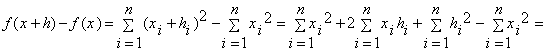
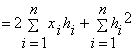 ,
,
причому
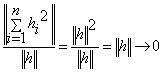 .
.
Лінійність:
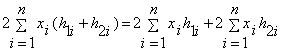 ,
, ![]() , тобто
, тобто ![]() ,
, ![]() ,
,
Обмеженість:
![]() .
.
Остаточно знаходимо, ![]() .
.
16. Довести, що необхідною і достатньою умовою диференційовності за Фреше відображення ![]() в точці x є диференційовність ( в звичайно-му сенсі) функції багатьох змінних
в точці x є диференційовність ( в звичайно-му сенсі) функції багатьох змінних ![]() в точці
в точці ![]() .
.
Доведення
Необхідність. Нехай відображення ![]() диференційовне за Фреше в точці x:
диференційовне за Фреше в точці x: 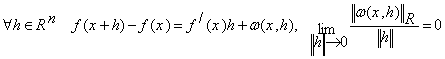 .
.
Функція ![]() в точці
в точці ![]() називається диференційовною, якщо
називається диференційовною, якщо
![]() ,(*)
,(*)
де ![]() .
.
Приведемо ![]() до вигляду (*):
до вигляду (*):
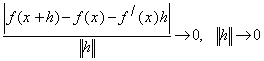 ,
, ![]()
![]() ,
, 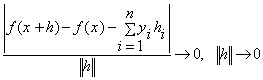
Виберемо ![]() , тоді
, тоді
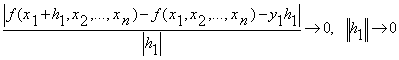
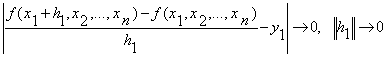
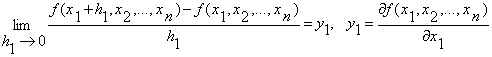
Виберемо ![]() , тоді знаходимо
, тоді знаходимо
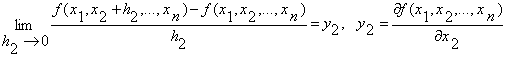 , і т.д.
, і т.д.
Виберемо ![]() , тоді
, тоді
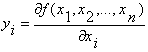 і
і
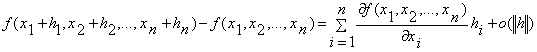 ,
,
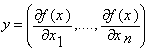 ,
, ![]() .
.
Достатність. Нехай відображення ![]() диференційовне в звичайному сенсі:
диференційовне в звичайному сенсі: ![]() . Перевіримо лінійність та обмеженість по h. Адитивність та однорідність для скалярного добутку вірні, тому лінійність є.
. Перевіримо лінійність та обмеженість по h. Адитивність та однорідність для скалярного добутку вірні, тому лінійність є.
Обмеженість:
![]() , де
, де ![]()
Остаточно знаходимо ![]() .
.
Розглянемо два приклади
1. ![]() ,
,
тоді
![]() ,
, ![]() .
.
2. ![]() , тоді
, тоді ![]()
17. Знайти похідну Фреше відображення ![]() в точці
в точці ![]() :
:
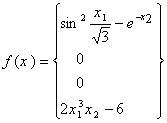
Розв’язок.
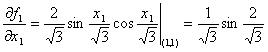 ;
;![]() ;
;
![]() ;
; ![]()
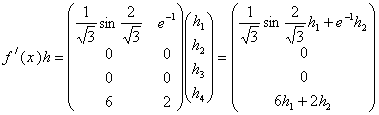
18. Нехай ![]() і
і 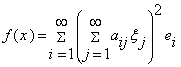 , де
, де ![]() – стандартний базис в
– стандартний базис в ![]() . Знайти похідну Гато
. Знайти похідну Гато ![]() .
.
Розв’язок
Якщо 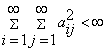 , то
, то ![]() відображає
відображає ![]() в
в ![]() . Дійсно, позначимо
. Дійсно, позначимо 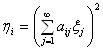 , ряд
, ряд ![]() збігається, тоді збігається й ряд
збігається, тоді збігається й ряд ![]() , так що
, так що ![]() для довільного
для довільного ![]() .
.
Обираємо за напрямок одиничного вектора орт ![]() і знаходимо
і знаходимо
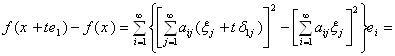
![]()
Тоді
![]()
Похідна ![]() існує і дорівнює
існує і дорівнює
![]() .
.
19. Якщо відображення диференційовне за Фреше, то воно диференційовне за Гато. Обернене твердження в загальному випадку невірне. Наприклад, в просторі ![]() розглянемо функцію
розглянемо функцію
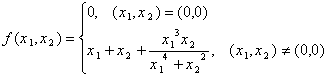
Дослідимо функцію на неперервність в точці (0,0):
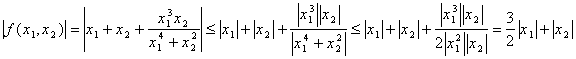
Якщо ![]() , то
, то![]() і
і ![]() . Тобто
. Тобто ![]() неперервна в точці (0,0).
неперервна в точці (0,0).
Розглянемо
![]()
![]()
Тобто, відображення ![]() диференційовне за Гато.
диференційовне за Гато.
Розглянемо
![]()
– функція двох змінних, покладемо ![]() , нехай
, нехай ![]() і розглянемо
і розглянемо
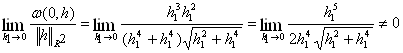 ,
,
тобто відображення ![]() не диференційне за Фреше.
не диференційне за Фреше.
20. Якщо диференціал Гато є обмеженим функціоналом, то він називається градієнтом функціонала і позначається ![]() .
.
Нехай Н – дійсний гільбертів простір, ![]() . Обчислити
. Обчислити ![]() .
.
Розв’язок
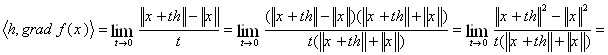

За теоремою про загальний вигляд лінійного функціонала в Н знаходимо, що
![]() .
.
21. Нехай Н – дійсний гільбертів простір, ![]() . Обчислити
. Обчислити ![]() .
.
Розв’язок

За теоремою про загальний вигляд лінійного функціонала в Н знаходимо, що
![]() .
.
22. Нехай Е – нормований простір. норма диференційовна за Гато. Розглянемо функціонал ![]() . Обчислити норму функціонала
. Обчислити норму функціонала ![]() .
.
Розв’язок
![]()
![]()
З одного боку ![]() , з іншого боку –
, з іншого боку – ![]() . Отже,
. Отже, ![]() , тобто
, тобто ![]() .
.
Розглянемо
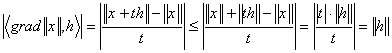 .
.
Переходячи до ![]() , нерівність зберігається:
, нерівність зберігається:
![]()
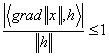 ,
, 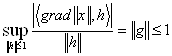 , отже
, отже ![]() .
.
23. Довести, що градієнт норми є непарним оператором, тобто довести співвідношення: ![]() .
.
Доведення
Нехай ![]() . Розглянемо
. Розглянемо

24. Нехай ![]() , де
, де ![]() неперервна за обома аргументами і неперервно диференційовна за другим аргументом, а
неперервна за обома аргументами і неперервно диференційовна за другим аргументом, а ![]() – неперервна функція. Знайти похідну Фреше в точці
– неперервна функція. Знайти похідну Фреше в точці ![]() .
.
Розв’язок
![]()
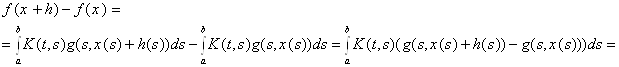
![]()
![]() ,
, ![]()
Відповідь:
![]() .
.
25. Знайти похідну Фреше наступних відображень в заданих точках:
1) ![]()
Згідно з задачею 24 ![]() , тоді
, тоді
![]() ,
, ![]() ,
, ![]() .
.
2) ![]()
Згідно з задачею 24 ![]() , тоді
, тоді
![]() ,
, ![]() ,
, ![]()
3) ![]()
Згідно з задачею 24 ![]() , тоді
, тоді
![]() ,
, ![]() ,
, ![]()
4) ![]()
Згідно з задачею 24 ![]() , тоді
, тоді
![]() ,
, ![]() ,
, ![]()
5) ![]()
Згідно з задачею 24 ![]() , тоді
, тоді
![]() ,
, ![]() ,
, ![]()
6) ![]()
Згідно з задачею 24 ![]() , тоді
, тоді
![]() ,
, ![]() ,
, ![]()
26. Нехай ![]() , де
, де ![]() неперервна за всіма аргументами і двічі неперервно диференційовна за третім аргументом. Знайти похідну Фреше в точці
неперервна за всіма аргументами і двічі неперервно диференційовна за третім аргументом. Знайти похідну Фреше в точці ![]() .
.
Розв’язок
![]()
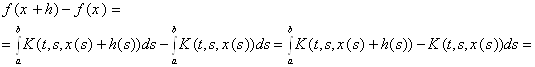
![]() ,
, ![]() ,
, ![]()
Відповідь:
![]() .
.
Похожие работы
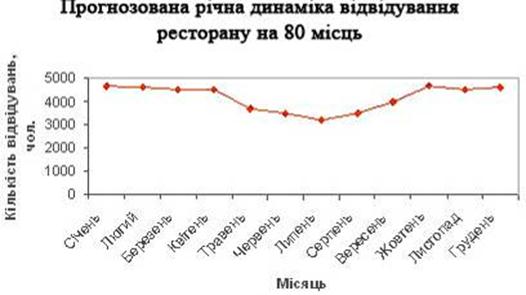
... Чарка, стакан 4 320 2 80 400 Столові прибори (комплект) 4 320 2 80 400 Далі наведемо характеристику посуду, який будуть використовувати в комплексному закладі ресторанного господарства (табл. 2.8–2.11). Таблиця 2.8. Характеристика та призначення класичного вітчизняного порцелянового та фаянсового посуду Найменування Розміри, мм Місткість, см3, порцій Призначення ...
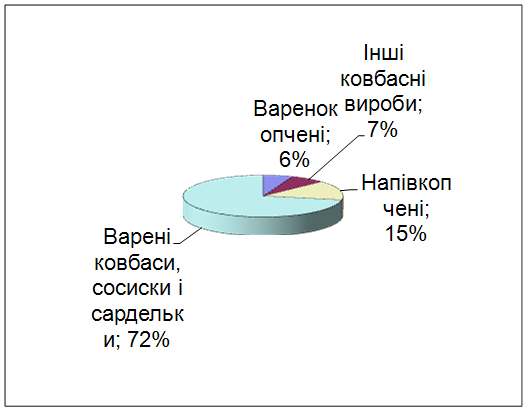
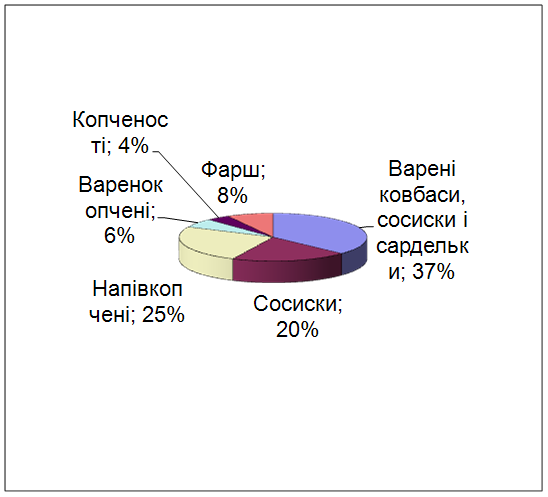
... ється, окремими технологічними операціями, специфічними виглядом і смаком, енергетичною цінністю та іншими ознаками. Варені ковбаси займають 53-60% в загальному виробництві ковбасних виробів. 3.1 Характеристика підприємства Ковбасний цех спільного підприємства Сумський виробничий комбінат розміщєно напівнічному-сході м. Суми, на відстані 1000 м від житлових кварталів. Окрім ковбасного цуху ...
0 комментариев