Навигация
РОБИНСОН И «НОВАЯ ИСТОРИЯ» НЕСТАНДАРТНОГО АНАЛИЗА
2. РОБИНСОН И «НОВАЯ ИСТОРИЯ» НЕСТАНДАРТНОГО АНАЛИЗА
В 1961 г. появилась статья А. Робинсона «Нестандартный анализ» в Трудах Нидерландской академии наук. В статье намечены как основные положения нестандартного анализа, так и некоторые его приложения (например, к аналитической механике). В этой статье Робинсон, в частности, писал: “Наша главная цель – показать, что эти модели дают естественный подход к старой почтенной проблеме построения исчисления, включающего бесконечно большие и бесконечно малые количества. Как хорошо известно, использование бесконечно малых, настойчиво защищаемое Лейбницем и без колебании принимаемое Эйлером, было дезавуировано с появлением методов Кошн, поставивших математический анализ на твердую основу”.
Итак, до 1961 г. понятие бесконечно малой поятоянной величины, бесконечно малого числа, интерпретировалось как в лучшем случае нестрогое, а в худшем — бессмысленное. Робинсон впервые обнаружил, что этому понятию можно придать точный математический смысл.
В течение последующих восьми лет вышли в свет три монографии, излагающие нестандартную теорию: в 1962 г.– книга У. Л. Дж. Люксембурга “Нестандартный анализ. Лекции о робинсоновой теории бесконечно малых и бесконечно больших чисел”, в 1966 г.— книга самого А. Робинсона “Нестандартный анализ”, в 1969 г. — книга М. Маховера и Дж. Хиршфелда “Лекции о нестандартном анализе”] (из 77 страниц этих “Лекций” действительной прямой отведено немногим болеее двух: «нестандартный анализ» понимается здесь в самом широком смысле).
Наибольший резонанс вызвала книга Робинсона. В девяти первых главах этой монографии содержалось как построение необходимого логико-математического аппарата, так и многочисленные приложения – к дифференциальному и интегральному исчислению, к общей топологии, к теории функций комплексного переменного, к теории групп Ли, к гидродинамике и теории упругости.
В 1966 г. появилась статья А.Р. Бернстейна и А. Робинсона, в которой впервые методами нестандартного анализа было получено решение проблемы инвариантных пространств для полиномиально компактных операторов. В очерке П.Р. Халмоша “Взгляд в гильбертово пространство” в качестве проблемы фигурирует поставленная К.Т. Смитом задача о существовании инвариантного подпространства для таких операторов Т в гильбертовом пространстве ![]() , для которых оператор
, для которых оператор ![]() компактен. А.Р. Бернстейном и А. Робинсоном методами нестандартного анализа было доказано, что любой полиномиально компактный оператор в гильбертовом пространстве имеет нетривиальное инвариантное замкнутое подпространство.
компактен. А.Р. Бернстейном и А. Робинсоном методами нестандартного анализа было доказано, что любой полиномиально компактный оператор в гильбертовом пространстве имеет нетривиальное инвариантное замкнутое подпространство.
Приложения нестандартного анализа в математике охватывают обширную область от топологии до теории дифференциальных уравнений, теории мер и вероятностей. Что касается внематематических приложений, то среди них мы встречаем даже приложения к математической экономике. Многообещающим выглядит использование нестандартного гильбертова пространства для построения квантовой механики. А в статистической механике становится возможным рассматривать системы из бесконечного числа частиц. Помимо применений к различным областям математики, исследования в области нестандартного анализа включают в себя и исследование самих нестандартных структур.
В 1976 г. вышли сразу три книги по нестандартному анализу: “Элементарный анализ” и “Основания исчисления бесконечно малых” Г. Дж. Кейслера и “Введение в теорию бесконечно малых” К. Д. Стройана и В. А. Дж. Люксембурга.
Быть может, наибольшую пользу нестандартые методы могут принести в области прикладной математики. В 1981 г. вышла книга Р. Лутца и М. Гозе “Нестандартный анализ: практическое руководство с приложениями”. В этой книге после изложения основных принципов нестандартного анализа рассматриваются вопросы теории возмущений.
В настоящее время нестандартный анализ завоёвывает всё большее признание. Состоялся ряд международных симпозиумов, специально посвященных нестандартному анализу и его приложениям. В течении последнего десятилетия нестандартный анализ (точнее, элементарный математический анализ, но основанный на нестандартном подходе) преподавался в ряде высших учебных заведений США.
3. БЕСКОНЕЧНО МАЛЫЕ ВЕЛИЧИНЫ
Один из наиболее принципиальных моментов нестандартного анализа состоит в том, что бесконечно малые рассматриваются не как переменные величины (т. е. не как функции, стремящиеся к нулю, как учат современные учебники), а как величины постоянные. Такой подход хорошо согласуется как с интуицией естествоиспытателя, так и с реальной историей зарождения математического анализа. Что касается интуиции, то достаточно раскрыть любой учебник физики, чтобы натолкнуться на бесконечно малые приращения, бесконечно малые объемы и т.п. Все эти величины мыслятся, разумеется, не как переменные, а просто как очень маленькие, почти равные нулю. Было бы неправильно считать подобного рода интуицию присущей лишь авторам учебников физики. Вряд ли какой-то математик воспринимает (наглядно) элемент дуги ds иначе, чем “очень маленькую дугу”. Любой математик, составляя соответствующее дифференциальное уравнение, скажет, что за бесконечно малое время dt точка прошла бесконечно малый путь dx, а количество радиоактивного вещества изменилось на бесконечно малую величину dN.
Что же касается истории математического анализа, то в наиболее явной форме излагаемый подход проявился у одного из основоположников этой науки — Лейбница. В мае 1984 г. исполнилось 300 лет с того дня, как символы dx и dy впервые появились на страницах математических публикаций, а именно в знаменитом мемуаре Лейбница “Новый метод...”. Именно Лейбниц яснее других ощущал бесконечно малые величины постоянными (хотя и воображаемыми, идеальными) величинами особого рода, и именно Лейбниц сформулировал правила оперирования с бесконечно малыми в виде исчисления.
Какие положительные числа следует называть бесконечно малыми?
Первый ответ таков: положительное число e называется бесконечно малым, если оно меньше всех положительных чисел. Однако бесконечно малых в этом смысле положительных чисел не бывает: ведь если число меньше всех положительных чисел и само положительно, оно должно быть меньше самого себя. Попытаемся исправить положение, потребовав, чтобы e было меньше всех других
положительных чисел, но больше нуля, т. е. чтобы e было наименьшим в множестве положительных чисел. На числовой оси такое e должно изобразиться самой левой точкой множества (0, +¥). К сожалению, числа e с указанными свойствами тоже нет и не может быть: если e положительно, то число e/2 будет положительным числом, меньшим e. (Согласно обычным свойствам неравенств для всякого а > 0 выполняются неравенства 0 < а/2 < а). Так что если мы не хотим отказываться от привычных нам свойств действительных чисел (например, от возможности разделить любое число на 2 или от возможности умножить любое неравенство на положительное число), но хотим иметь бесконечно малые числа, то приведенное определение бесконечной малости не годится.
Более изощренное определение бесконечной малости числа e > 0, которое мы будем использовать в дальнейшем, таково. Будем складывать число e с самим собой, получая числа e, e + e, e + e+ e, e + e + e +e и т. д. Если все полученные числа окажутся меньше 1, то число e и будет называться бесконечно малым. Другими словами, если e бесконечно мало, то сколько раз ни откладывай отрезок длины e вдоль отрезка длины 1, до конца не дойдешь. Наше требование к бесконечно малому e можно переписать и в такой форме (поделив на e): 1<1/e, 1+1<1/e, 1+1+1<1/e,…
Таким образом, если число число e бесконечно мало, то число 1/e бесконечно велико в том смысле, что оно больше любого из чисел 1, 1+1, 1+1+1, 1+1+1+1 и т. д. Так что если мы начнем измерять отрезок длиной 1/e с помощью эталона длины (т.е. откладывая последовательно отрезки единичной длины), то процесса измерения никогда не закончим.
Из вышеизложенного следует, что существование бесконечно малых противоречит так называемой аксиоме Архимеда, которая утверждает, что для любых двух отрезков А и В можно отложить меньший из них (А) столько раз, чтобы в сумме получить отрезок, превосходящий по длине больший отрезок (В).
Приведенная формулировка касается отрезков; если считать (как это обычно делается), что длины отрезков являются числами, мы приходим к такой формулировке аксиомы Архимеда: для любых двух чисел а и b, для которых 0 < а < b, одно из неравенств а + а > b, a + а + a > b, ... обязательно выполнено. В дальнейшем, говоря об аксиоме Архимеда, мы будем иметь в виду именно эту формулировку. Из нее видно, что в множестве действительных чисел (где эта аксиома выполняется) бесконечно малых нет: чтобы убедиться в этом, достаточно положить a=e, b=1. Мы увидим в дальнейшем, что на самом деле аксиома Архимеда равносильна утверждению об отсутствии бесконечно малых элементов, не равных нулю.
Вывод – если мы хотим рассматривать бесконечно малые, нужно расширить множество R действительных чисел до некоторого большего множества *R. Элементы этого нового множества будем называть гипердействительными числами. В нем аксиома Архимеда не выполняется и существуют бесконечно малые (в смысле последнего определения) числа — такие, что сколько их ни складывай с собой, сумма будет все время оставаться меньше 1. Подобно тому как обычный (или стандартный) математический анализ занимается изучением множества действительных чисел R, нестандартный анализ изучает множество гипердействи-тельных чисел *R. Полученные при этом результаты используются для исследования свойств R. (Таким образом могут быть получены “нестандартные” доказательства свойств обыкновенных действительных чисел.)
Порядок на R архимедов, а на *R неархимедов: это значит, что в R аксиома Архимеда выполняется, а в *R не выполняется. По этой причине стандартный (обычный) анализ, изучающий R, называется еще архимедовым, а нестандартный анализ, изучающий *R, называют неархимедовым.
Для построения нестандартного анализа необходимо расширить множество действительных чисел до более широкого множества гипердействительных чисел.
Но прежде поговорим о самих действительных числах и их происхождении.
До сих пор мы предполагали известным понятие действительного числа. Понятие действительного числа имеет долгую историю, начавшуюся еще в древней Греции (о чем напоминает название “аксиома Архимеда”) и закончившуюся лишь в XIX веке. Самой первоначальной и основной числовой системой является, конечно, система натуральных чисел. Натуральных чисел, однако, оказывается мало: пытаясь решить уравнение 3 + х = 2 в натуральных числах, мы обнаруживаем, что оно не имеет решений и наше желание определить операцию вычитания оказывается неудовлетворенным. Поэтому мы расширяем множество натуральных чисел до множества целых чисел. В этой процедуре для нас сейчас важно следующее: каким образом мы определим сложение и умножение на целых числах? То, что 2 + 2 == 4, можно увидеть, сложив две кучи по два яблока в одну. Но почему мы считаем, что (-2)+(-2)=(-4)? Почему мы считаем, что (-1)(-1)=1?
Эти вопросы не так тривиальны, как может показаться. Найти правильный ответ будет легче, если сформулировать вопрос иначе: что плохого произойдет, если мы будем считать, например, что (-1)(-1)=(-1)? Ответ прост: в этом случае хорошо известные свойства сложения и умножения натуральных чисел (коммутативность, ассоциативность и др.) не будут выполняться для целых чисел. Можно показать, что обычное определение операций над отрицательными числами единственно возможное, если мы хотим сохранить привычные свойства операций сложения и умножения.
Тут следует остановиться: какие же именно свойства сложения и умножения мы хотим сохранить? Ведь если бы мы хотели сохранить все свойства, то введение отрицательных чисел было бы не только излишне, но и вредно: свойство “уравнение х+3=2 не имеет решений”, верное для натуральных чисел, становится неверным для целых! Если же мы ничего не хотим сохранить, то задача становится столь же легкой, сколь и пустой: можно определить операции с отрицательными числами как угодно.
Возвращаясь к истории развития понятия числа, мы видим, что введение отрицательных чисел не доставляет полного удовлетворения: уравнение 2x=3 по-прежнему не имеет решения. Это побуждает ввести рациональные (дробные) числа. Но и этого недостаточно: от рациональных чисел приходится перейти к действительным. В результате получается последовательность множеств NÌZÌQÌR (натуральных, целых, рациональных и действительных чисел; АÌ В означает, что всякий элемент множества А принадлежит множеству B. В этой последовательности каждое следующее множество включает в себя предыдущее, при этом имевшиеся в предыдущем операции продолжаются на следующее, более широкое, множество, сохраняя свои полезные свойства.
Мы хотим продолжить эту последовательность еще на одни член, получив последовательность NÌZÌQÌRÌ*R, где *R – множество гипердействительных чисел. Новый шаг расширения будет иметь много общего с предыдущими: мы продолжим на *R имеющиеся в R операции, сохранив их полезные свойства. Но будут и 2 важных отличия.
Во-первых, если расширение (переход от R к *R) можно выполнить многими различными способами: можно построить существенно различные множества *R, ни одно из которых ничем не выделяется среди остальных. В то жо время, все предыдущие шаги нашего расширения числовой системы от N к R были в некотором смысле однозначны.
Во-вторых, есть различие в наших целях. Если прежде (двигаясь от N к R) мы строили новую числовую систему прежде всего для того, чтобы исследовать ее свойства и ее применения, то построенная система *R предназначается не столько для того, чтобы исследовать ее свойства, сколько для того, чтобы с ее помощью исследовать свойства R. Впрочем различие и не так велико: и раньше расширение числовой системы было одним из способов получения новых знаний о старых объектах. Кроме того, множество *R можно рассматривать, быть может, как соответствующее физической реальности в не меньшей (и даже в большей) степени, чем R.
Итак, необходимо расширить множество R действительных чисел до большего множества *R, содержащего бесконечно малые, сохранив при этом все полезные свойства R. Центральный вопрос состоит в том, какие именно свойства действительных чисел мы желаем сохранить. Ответим на этот вопрос не сразу, начав с наиболее простых свойств действительных чисел.
Прежде всего, мы хотим, чтобы гипердействительные числа можно было складывать, умножать, вычитать и делить, чтобы эти операции обладали обычными свойствами, называемыми «аксиомами поля». Сформулируем их.
Среди гипердействительных чисел должны быть выделены числа 0 и 1; определены операции сложения, умножения взятия противоположного, а также операция взятия обратного. При этом должны выполняться такие свойства:
(1) a+b=b+a (2) a+(b+c)=(a+b)+c (3) a+0=a (4) a+(-a)=0 (5) ab=ba
(6) a(bc)=(ab)c (7) a*1=a (8) a(b+c)=ab+ac (9) a*(1/a)=1 при a<>0.
Множество с операциями, обладающими этими свойствами, называется полем. Требования (1)-(9) можно сформулировать так: *R должно быть полем.
Кромеарифметических операций, зададим на гипердействительных числах порядок. Для любых двух различных гипердействительных чисел должно быть определено какое из них больше. При этои должны выполняться такие свойства:
(10) если a>b, b>c, то a>c
(11) если a>b, то a+c>b+c для любого с
(12) если a>b, c>0, то ac>bc
если a>b, c<0, то ac<bc
Поле, в котором введен порядок с такими свойствами, называется упорядоченным полем. Требования (10)-(12) можно сформулировать так: *R должно быть упорядоченным полем.
Мы хотим, чтобы среди гипердействиетльных чисел были все действительные. При этом операции и порядок на R и на *R должны быть соглсованы. Это требование можно сформулировать так: упорядоченное поле *R должно быть расширением упорядоченного поля R.
Что же нового мы ожидаем от *R? Бесконечно малых.
Определение. Элемент e>=0 упорядоченного поля называется бесконечно малым, если e<1, e+e<1. e+e+e<1 и т.д. Отрицательное e называется бесконечно малым, если –e бесконечно мало.
Существование ненулевых бесконечно малх равносильно нарушению аксиомы Архимеда для гипердействительных чисел. Упорядоченные поля, в которых справедлива аксиома Архимеда и нет бесконечно малых, называют архимедово упорядоченными. Те поля, в которых аксиома Архимеда невернаи есть бесконечно малые, называют неархимедово упорядоченными (неархимедовым).
В этих терминах треюования можно сформулировать так: система гипердействительных чисел должна быть неархимедово упорядоченным полем, являющимся расширением упорядоченного поля действительных чисел.
Похожие работы
... состоит из значений функции g(x) на отрезке [a,b]. Причём этот оператор имеет лишь непрерывный спектр, так как резольвента при существует, но не непрерывна. Точечного спектра оператор не имеет. Пример 3: Рассмотрим оператор дифференцирования на множестве дифференцируемых функций. А: (для краткости будем писать вместо f(x) просто f). Рассмотрим резольвенту этого оператора: , то есть мы должны ...
... «Математических лекциях о методе интеграла»[9]. Здесь дан способ взятия большинства элементарных интегралов и указаны методы решения многих дифференциальных уравнений первого порядка. 2 Вклад Л.Эйлера в развитие математического анализа Леонард Эйлер (Euler, Leonhard) (1707–1783) входит в первую пятерку величайших математиков всех времен и народов. Родился в Базеле (Швейцария) 15 апреля ...
... динамике и соотношениям, которые связывают его с другими управляющими параметрами, характеризующими человеческое общество [7-10 ]. Можно установить непосредственную связь этого параметра с некоторой физической мерой, характеризующей как отдельного человека, так и человечество в целом, которая связывает этот биологический вид со всеми живыми и неживыми объектами природы – этой мерой является масса ...
... у детей. Дети бережнее относится к инвентарю, повышается плотность урока, повышается качество обучения. Так же при использовании такого оборудования происходит влияние на формирование интереса младшего школьного возраста на уроках физической культуры. Происходит удовлетворение интереса, который может укрепляться, развиваться, становиться более глубоким и разносторонним. Интерес, таким образом, ...
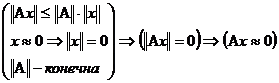


0 комментариев