НОВЫЕ ТРЕБОВАНИЯ К ГИПЕРДЕЙСТВИТЕЛЬНЫМ ЧИСЛАМ И ОСНОВНАЯ ГИПОТЕЗА

6. НОВЫЕ ТРЕБОВАНИЯ К ГИПЕРДЕЙСТВИТЕЛЬНЫМ ЧИСЛАМ И ОСНОВНАЯ ГИПОТЕЗА

Мы построили неархимедово расширение R(e) поля действительных чисел. Новым требованием к гипердействительным числам яляется следующее. Нужно уметь вычислять «значения» стандартных функций (заданных первоначально как функции с дей­ствительными аргументами и значениями) на гипердействительных аргументах. Другими словами, для каждой функции f: R®R необходимо иметь ее «гипердействптельный аналог» *f: R®R. При этом, значения *f на стандартных числах должны совпадать с соответствующими значениями функции f. Другими сло­вами, *f должно быть продолжением f. Такие аналоги были у нас для операций сложения, вычитания, умно­жения и деления. Но этого мало: нужны такие ана­логи и для других функций.

Итак, для каждой стандартной функции f (функции с действительными аргументами и значениями) нам нуж­но иметь ее гипердействительное продолжение *f. Если от *f ничего не требовать, то это тривиально: можно счи­тать, что во всех действительных точках *f принимает те же значения, что и f, а в нестандартных точках *f имеет какие угодно значения (например, нули). Ясно, однако, что от такого продолжения никакого толку нет:

Нужно выделить некоторый класс свойств — класс тех свойств, которые мы хотим сохранить. Правильный выбор этого класса имеет решающее значение для успеха нашего построения системы гипердействительных чисел. Если этот класс будет слишком узок, то от наличия продолжений *f не будет пользы. Если же, напротив, он будет слишком широк, то сама возможность построения системы гипердействительпых чисел и определения продолжений окажется под угрозой.

Наша главная задача – описать, какие свойст­ва стандартных функций мы хотим сохранить при пере­ходе от действительных чисел к гипердействительным. Есть две возможности это сделать. Первая возможность состоит в применении методов математической логики. Можно сказать, что при переходе от действительных чи­сел к гипердействительным сохраняются все свойства, которые можно выразить на «языке первого порядка». Вторая возможность позволя­ет обойтись более «кустарными» средствами и не при­бегать к сведениям из логики. Конечно, при этом мы будем испытывать некоторые неудобства, использовать обходные маневры и т. п., но зато не потребуется зна­комство с математической логикой.

Мы предполагаем, что помимо поля R действительных чи­сел имеется более широкое упорядоченное поле *R гипердействительных чисел, включающее R как подмно­жество (еще раз подчеркнем, что существование *R с нужными свойствами является пока только гипотезой, а не доказанным фактом). Пусть для каждой функции f с действительными аргументами имеется ее естественное распространение, ее «гипердействительный аналог» — функция с гипердействительными аргументами и значе­ниями. При этом функция f может быть функцией не только одного действительного аргумента, но и двух, трех и т. д.; функция *f, разумеется, должна иметь то же самое число аргументов. Для простоты мы пока не будем рассматривать частичных функций и будем счи­тать, что f (соответственно *f) определена при всех действительных (соответственно гипердействительных) аргументах. Сформулируем теперь наше требование («ана­логи обладают теми же свойствами, что и исходные функ­ции») более точно.

Будем рассматривать системы уравнений вида t=s и неравенств вида t¹s, левые и правые части которых содержат какие-то действительные функции действитель­ных аргументов, действительные константы и перемен­ные — что-нибудь вроде

sin(cos(x))=y+exp(z), z¹y-2x, [z]=y

Эта система содержит переменные x, y, z, одноместные функции sin,cos,exp [ ] (целая часть), двуместные функции (сложение, вычитание, умножение) и констан­ту 2 (константы для единообразия мы будем считать функциями нуля аргументов). Все входящие в систему функции имеют по нашему предположению гипердействительные аналоги. Обозначим их *sin, *cos, *exp, *[ ], *+, *–, и напишем систему

*sin(*cos(x))=y*+*exp(z), z¹y*–2*x, *[z]=y

которую естественно назвать «гипердействительным аналогом исходной».

В качестве возможных значении переменных этой системы могут фигурировать любые гипердействительные числа. Тем самым приобретает смысл вопрос о наличии или отсутствии гипердействительных решений этой системы. Поскольку мы предполагаем, что входящие в нее функции являются продолжениями соответствующих функций действительного аргумента, то всякое (действительное) решение исходной системы будет одновременно решением новой системы. Таким образом, если исход­ная система имеет решения, то и ее гипердействительный аналог имеет решения. Мы потребуем и обратного:

всякая система уравнений и неравенств, гипердействительный аналог которой имеет (гипердействительные) решения, должна иметь действительные решения.  

Введем понятие терма. Выберем счетный набор символов, элементы которого будем называть переменными. Будем назы­вать термом любую переменную, любое действительное число, а также любое выражение вида f(t₁, ..., t_n), где f – функция п действительных аргументов, а t₁, ..., t_n – построенные ранее термы.

Системой (точнее, системой уравнений и нера­венств) назовем конечный набор записей вида t=s или t¹s, где t, s – термы. Определим теперь понятие решения системы. Еслп в терм подставить действительные числа вместо переменных, то он приобретет некоторое действительное значение. Решение системы – это такой набор значений переменных, при ко­тором левая и правая части любою равенства I t=s, вхо­дящего в систему, приобретают одно и то же значение, а левая и правая части любого неравенства t¹s, входяще­го в систему,— разные.

По нашему предположению всякая функция с дейст­вительными аргументами н значениями имеет гппердействительный аналог («естественное продолжение»). По­нятие гипердействительного аналога легко распространя­ется на термы — чтобы получить аналог терма t, надо просто заменить все входящие в него функции на их гипердействительпые аналоги. Проделав эту операцию со всеми термами, входящими в какую-то систему S, мы по­лучим систему *S, которую естественно также назвать гипердействительным аналогом системы S. Поскольку в нее входят функции с гипердействительными аргумента­ми и значениями, вместо переменных можно подставлять произвольные гипердействительные числа. Гппердейст-вительным решением системы *S назовем такой набор гипердействительпых значений переменных, при которых выполнены все входящие в нее уравнения и неравенства. Теперь можно сформулировать наше требование к систе­ме гипердействительных чисел и к гипердействительным аналогам следующим образом.

Пусть S — произвольная система уравнений и неравенств, *S – ее гипердействительный аналог. Если *S имеет (гипердействительные} решения, то S долж­на иметь действительные решения.

Возможность построения неархимедо­ва упорядоченного расширения *R поля R и таких гипердействительных аналогов *f для всех действительных функций f, которые бы удовлетворяли сформулированному требованию, остается пока всего, лишь гипотезой. (Мы будем называть эту гипотезу Основной гипотезой.)

Приведем несколько примеров, показывающих, какие следствия можно вывести из сфор­мулированной Основной гипо­тезы. Оказывается, что несмотря на то, что сформулиро­ванное нами требование одновременной разрешимости систем уравнений и неравенств кажется весьма частным, оно имеет самые разнообразные следствия и достаточно для обоснований значительной части рассуждений с ги-пердействительными числами.

Пример 1. Пусть f – функция одного действитель­ного аргумента, принимающая только значения 0 и 1. Докажем, что функция *f принимает только значения 0 и 1. Для этого рассмотрим систему

f(x)¹0, f(x)¹1,

которая по предположению не имеет действительных решений. Следовательно, не имеет (гипердействительных) решений и ее аналог — система

*f(x)¹0, *f(x)¹1,

Пример 2. Пусть f и g – функции одного действительного аргумента, причем множества их нулей совпа­дают. (Множество нулей функции – множество тех зна-чений аргумента, при которых значение функции равно 0) В этом случае и множества гипердействительных чисел, являющиеся множествами нулей функций *f и *g, совпадают. Докажем это. В самом деле, каждая из си­стем

(1) f(x)=0, g(x)¹0,

(2) g(x)=0, f(x)¹0,

не имеет действительных решений. Следовательно, не имеют гииердействительных решений и их аналоги. По­тому любой гипердействительный нуль функции *f обя-зан (чтобы не быть решением аналога системы (1)) быть нулем и для *g и наоборот.

Этот пример позволяет определить гипердействительные аналоги не только для функций, но и для множеств.

Пусть А – произвольное множество действительных чисел. Рассмотрим произвольную функцию f, для которой А – множество нулей. (Такая есть: достаточно положить, например, f(x)=0 при хÎА и f(x)=1 при xÏA). Рассмотрим теперь гипердействительный аналог *f функции f и множество *А его (гипердействительных) нулей. Как мы видим, множество *А не зависит от выбора функ­ции f. Его мы и назовем гипердействительным аналогом множества А.

Пример 3. Мы можем теперь разрешить включать системы наряду с равенствами t=s и неравенст­вами t¹s и записи вида sÎA, где s представляет собой терм, а А – множество действительных чисел. При этом решениями будут такие наборы (действительных или гипердействительных) значений переменных, при ко­торых выполнены все равенства и неравенства, а значе­ние s принадлежит множеству А. Гипердействительным аналогом sÎA будет *sÎ*A, где *s – гипердей-ствительный аналог терма s, а *A — аналог множества А (в указанном смысле). Таким образом, у всякой си­стемы равенств, неравенств и включений (т. е. записей вида sÎA) появляется гипердействительный аналог. Для таких систем остается в силе свойство одновременной разрешимости: если гипердействительный аналог систе­мы имеет (гипердействительные) решения, то исходная система имеет (действительные) решения. Чтобы уви­деть это, достаточно заменить sÎA на a(s)=0, где a – функция с действительными аргументами и значениями, множеством нулей которой является A. Аналогичным об­разом можно добавлять в систему и утверждения вида sÏA (что заменяется на a(s)¹0).

Пример 4. Пусть А – пустое множество. Докажем, что *A – пустое множество.

В самом деле, система

хÎА

не имеет действительных решений, поэтому и система хÎ*А не имеет (гипердействительных) решений. Рас­смотрев систему хÏА, получаем аналогичным образом, что если А содержит все действительные числа, то *А содержит все гипердействительные числа. Таким обра­зом, гипердействительным аналогом множества R будет множество *R, так что наши обозначения согласованы.

Вдальнейшем, вместо того чтобы говорить о системе S и ее действительных решениях, а также о системе *S и ее гипердействительных решениях, будем говорить о дейст­вительных и гипердействительных решениях системы S (говоря о гипердойствительных решениях системы S, мы на самом деле будем иметь в виду гипердействительные решения системы *S).

Пример 5. Если A=BÇC, то *A=*BÇ*C. В самом деле, каждая из систем

хÎB, хÎС, хÏА;

хÎA, хÏB;

хÎA, хÏС.

не имеет действительных, и, следовательно, гипердейст­вительных решений. (Точнее, следовало бы говорить об аналогах этих систем) Отсюда получаем, что *В Ç*С Ì *A (первая система), *АÌ*С (вторая) и *AÌ*C (третья), откуда вытекает, что *AÌ*BÇ*C.

Наши требования к системе гипердействительных чисел состояли из двух частей. Во-первых, *R должно быть упорядоченным неархимедовым полем, расширяющим R. Во-вторых, должны существовать ана­логи для всех действительных функций, удовлетворяю­щие требованию одновременной разрешимости систем уравнений. Эти требования оказываются избыточными:

тот факт, что гипердействительные аналоги сложения, умножения и т. п. превращают *R в поле, можно выве­сти из требования одновременной разрешимости систем уравнений.

Похожие работы

Спектр оператора. Применение нестандартного анализа для исследования резольвенты и спектра оператора

Скачать

36187

0

5

... состоит из значений функции g(x) на отрезке [a,b]. Причём этот оператор имеет лишь непрерывный спектр, так как резольвента при  существует, но не непрерывна. Точечного спектра оператор не имеет. Пример 3: Рассмотрим оператор дифференцирования на множестве дифференцируемых функций. А: (для краткости будем писать вместо f(x) просто f). Рассмотрим резольвенту этого оператора: , то есть мы должны ...

Вклад Л.Эйлера в развитие математического анализа

Скачать

31365

0

0

... «Математических лекциях о методе интеграла»[9]. Здесь дан способ взятия большинства элементарных интегралов и указаны методы решения многих дифференциальных уравнений первого порядка.   2 Вклад Л.Эйлера в развитие математического анализа   Леонард Эйлер (Euler, Leonhard) (1707–1783) входит в первую пятерку величайших математиков всех времен и народов. Родился в Базеле (Швейцария) 15 апреля ...

Человечество. Некоторые нестандартные модели

Скачать

36641

1

3

... динамике и соотношениям, которые связывают его с другими управляющими параметрами, характеризующими человеческое общество [7-10 ]. Можно установить непосредственную связь этого параметра с некоторой физической мерой, характеризующей как отдельного человека, так и человечество в целом, которая связывает этот биологический вид со всеми живыми и неживыми объектами природы – этой мерой является масса ...

Влияние использования нестандартного оборудования на формирование интереса младшего школьного возраста на уроках физической культуры

Скачать

69900

4

3

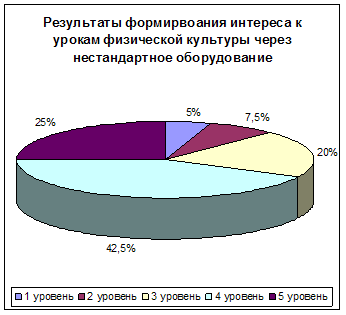
... у детей. Дети бережнее относится к инвентарю, повышается плотность урока, повышается качество обучения. Так же при использовании такого оборудования происходит влияние на формирование интереса младшего школьного возраста на уроках физической культуры. Происходит удовлетворение интереса, который может укрепляться, развиваться, становиться более глубоким и разносторонним. Интерес, таким образом, ...