Навигация
ГИПЕРДЕЙСТВИТЕЛЬНАЯ ПРЯМАЯ
4. ГИПЕРДЕЙСТВИТЕЛЬНАЯ ПРЯМАЯ
Предположим, что неархимедово расширение упорядоченного поля действительных чисел существует. Исследуем его свойства.
Пусть *R – неархимедово расширение R. Его элементы называются гипердействительными числами. Среди них содержатся и все действительные числа. Для отличия тех гипердействительных чисел, которые не являются действительными (элементы R) назовем их стандартными, а остальнгые гипердействительные (элементы *R\R) – нестандартными. Тогда бесконечно малые являются нестандартными, так как среди действительных чисел бесконечно малых нет.
Бесконечно малые положительные числа меньше всех стандартных положительных чисел. Аналогичным образом отрицательные бесконечно малые числа больше всех стандартных отрицательных чисел. Таким образом, если пытаться изобразить бесконечно малые числа на числовой прямой, то пришлось бы втиснуть их настолько близко к нулю, чтобы все положительные стандартные числа оказались справа, а отрицательные – слева.
Указанное свойство может служить определением бесконечной малости: если число e>0 меньше всех стандартных положительных чисел, то оно бесконечно мало.
Определение. Гипердействительное число А>0 называется бесконечно большим, если А>1, А>1+1, А > 1+1+1, .…(Отрицательное число В называется бесконечно большим, если таков его модуль)
Положительное бесконечно большое число А больше любого стандартного.
Аналогичным образом всякое отрицательное бесконечно большое гипердействительное число меньше любого стандартного.
Определение. Гипердействительные числа, не являющиеся бесконечно большими, будут называться конечными.
Утверждение. Если s – конечное гипердействительное число, то найдутся стандратное v и бесконечно малое e, для которых s=v+e. Такое представление единственно.
Определение. Стандартной частью st(x) конечного гипердействительного числа x называется такое стандартное v, что x=v+e для бесконечно малого e.
Гипердействительная прямая разбивается на 3 части (слева направо): отрицательные бесконечно большие, конечные, положительные бесконечно большие. Рассмотрим «конечную часть» гипердейсьвительной прямой. Рядом с каждым стандартным действительным числом а расположено множество бесконечно близких к нему гипердействительных чисел, для которых а является стандратной частью. Это множество называют монадой стандартного числа а. Множество конечных гипердействительных чисел разбито на непересекающиеся классы – монады, соответствующие стандартным действительным.
Сумма и разность бесконечно малых бесконечно малы, произведение бесконечно малого и конечного гипердействительных чисел бесконечно мало.
Определение. Два гипердействительных числа называются бесконечно близкими, если их разность бесконечно мала.
Из приведенных выше свойств бесконечно малых следует, что отношение бесконечной близости есть отношение эквивалентности. Это означает, что отношение бесконечно близости рефлексивно (каждое x бесконечно близко самому себе), симметрично (если x бесконено близко к y, то y бесконечно близко к x) и транзитивно (если x бесконено близко к y, а y бесконечно близко к z, то x бесконечно близко к z). Всякое отношение эквивалентности разбивает множество, на котором оно определено на непересекающиеся классы, причем любые два элемента одного класса эквивалентны, а любые два элемента разных классов не эквивалентны. В частности, наше отношение разбивает *R на непересекающиеся классы, причем элементы одного класса бесконечно близки друг к другу, а элементы разных классов — нет. Классы, содержащие стандартные действительные числа, представляют собой упоминавшиеся выше «монады».
5. ПРИМЕР НЕАРХИМЕДОВОЙ ЧИСЛОВОЙ СИСТЕМЫДо сих пор речь шла о гипердействительной прямой (а точнее, любом неархимедовом расширении упорядоченного поля действительных чисел). Возникает вопрос – существует ли хотя бы одно такое распшрение. Построим такое расширение.
Основная идея этого построения может быть описана в одной фразе так: у нас нет объектов, но есть имена для них; так объявим же имена объектами! Эта (часто применяемая в математической логике) идея конкретизируется в нашем случае следующим образом.
Мы знаем, что в нашем (пока еще не построенном и неизвестно существующем ли) расширении должно быть хотя бы одно бесконечно малое положительное гипердействительное число. Обозначим его через e. Поскольку гипердействительные числа можно умножать друг на друга (и, в частности, на действительные числа), то наряду с e в нашем расширении будут и числа 2e, 0,5e и вообще все числа вида ae, где а – произвольное стандартное действительное число. Более того, число e можно умножать и на себя, поэтому в нашем расширении будут иметься e2, e3, 2e2, Зe2+2e+1, ... и вообще все гипердействительные числа вида Р(e), где P – многочлен со стандартными действительными коэффициентами.
Множество чисел такого вида замкнуто относительно сложения, вычитания и умножения. Это значит, что, складывая, вычитая или перемножая два числа такого вида, мы вновь получим число такого же вида. Но для гипердействительных чисел определено еще и деление. Поэтому в расширении будут и числа вида Р(e)/Q(e), где P и Q – многочлены со стандартными действительными коэффициентами. После этого мы получаем множество гипердействптельных чисел, замкнутое относительно всех арифметических операций: складывая, вычитая, умножая или деля две дроби указанного вида по обычным правилам, получаем дробь такого же вида.
Таким образом, не имея пока искомого расширения, мы уже смогли назвать некоторые его элементы, дать им имена. Этими именами являются записи вида P(e)/Q(e), где e – некоторый символ. Более того, мы можем судить и о том, какая из двух записей обозначает большее число. В самом деле, достаточно уметь определять, обозначает ли данная запись положительное, отрицательное или нулевое число (поскольку а > b тогда и только тогда, когда a-b>0). Знак дроби можно определить по знакам числителя и знаменателя, следовательно достаточно уметь определять знак P(e), где Р – многочлен. Это делается так. Легко видеть, что знак величины a0+a1e+… совпадает со знаком a0, если a0<>0. В самом деле, добавка a1e+… бесконечно мала, а складывая положительное (отрицательное) число с бесконечно малым, мы получаем положительное (соответственно отрицательное) число. Возможен, однако, случай a0=0. Будем считать для определенности, что e – положительное бесконечно малое. Вынесем из нашего многочлена e в наибольшей возможной степени, т. е. представим его в виде ek(ak+ak+1e+…), где akуже отлично от 0. Знак всего выражения определяется знаком выражения в скобках (при умножении на положительное число знак не меняется), а знак выражения в скобках (как мы уже видели) определяется знаком числа ak..
По существу, мы уже построили искомое неархимедово расширение. Нужно лишь посмотреть на наши рассуждения с другой позиции. До сих пор выражения P(e)/Q(e) рассматривались нами как имена «настоящих» гипердействительных чисел (взятых неизвестно откуда). А теперь они станут самими гипердействительными числами. Рассмотрим формальные выражения вида P(e)/Q(e), где e – некоторый символ, P, Q – многочлены с действительными коэффициентами, причем Q<>0. Провозглашая, что объектами, а в данном случае гипердействительными числами, мы объявим имена, а в данном случае выражения, или записи вида P(e)/Q(e), мы были не совсем точны. Дело в том, что, очевидно, две различные записи могут выражать одно и то же число (иными словами, быть двумя различными именами одного и того же числа): так, например, естественно считать, что запись (e2-1)/(e-1) выражает то же самое число, что и (e+1)/1.
Будем называть два выражения P(e)/Q(e) и R(e)/S(e) эквивалентными, если P(e)*S(e)=R(e)*Q(e) (равенство понимается как равенство многочленов, т. е. как равенство коэффициентов при одинаковых степенях). Легко проверить, что это определение действительно задает отношение эквивалентности, разбивающее все выражения вида P(e)/Q(e) на классы. Эти классы мы и будем называть гипердействительными числами. Сложение, вычитание, умножение и деление гипердействительных чисел определяются по обычным правилам. Так, например, если a – класс, содержащий P/Q, а b – класс, содержащий R/S, то их суммой называется класс, содержащий (PS+RQ)/SQ, а произведением — класс, содержащий PR/QS. Легко проверить, что это определение корректно, т. е. не зависит от выбора элементов P/Q в классе a и R/S в классе b (в результате получаются разные представители одного и того же класса). Аналогичным образом можно определить взятие обратного и противоположного, нуль и единицу. Нетрудно проверить, что все аксиомы поля при этом будут выполнены. Изложенная конструкция хорошо известна в алгебре: построенное поле называется полем рациональных функций с коэффициентами в R и обозначается R(e).
Осталось определить только порядок, указав, как выбрать из двух различных гипердействительных чисел (т. е. из двух различных классов эквивалентных дробей) большее. Для этого нужно вычесть одно число из другого и определить, будет ли разность (отличная от нуля, поскольку числа различны) положительной или отрицательной. Чтобы определить, будет ли отличное от нуля число a положительным или отрицательным, возьмем его представитель P/Q. Здесь P, Q отличны от 0 (Q отлично от нуля по определению, Р – потому что, по нашему предположению, разность не равна 0). Вынесем в числителе и в знаменателе e в наибольшей возможной степени:
P=ek(ak+ak+1e+…), Q=el(bl+bl+1e+…), ak, bl отличны от 0.
Число a будет положительным, если ak, bl имеют одинаковые знаки, и отрицательным, если они имеют разные знаки.
Построенное упорядоченное поле R(e) можно рассматривать как расширение поля R: достаточно отождествить действительное число х с классом эквивалентных дробей, содержащим дробь x/1. Осталось лишь показать, что аксиома Архимеда не выполняется, предъявив бесконечно малый элемент. Этим элементом будет, конечно, e (точнее, класс, содержащий e/1). В самом деле, e+e+ ... +e <1, так как разность 1-ne положительна (знак определяется свободным членном, а 1 > 0).
Искомое расширение построено.
Похожие работы
... состоит из значений функции g(x) на отрезке [a,b]. Причём этот оператор имеет лишь непрерывный спектр, так как резольвента при существует, но не непрерывна. Точечного спектра оператор не имеет. Пример 3: Рассмотрим оператор дифференцирования на множестве дифференцируемых функций. А: (для краткости будем писать вместо f(x) просто f). Рассмотрим резольвенту этого оператора: , то есть мы должны ...
... «Математических лекциях о методе интеграла»[9]. Здесь дан способ взятия большинства элементарных интегралов и указаны методы решения многих дифференциальных уравнений первого порядка. 2 Вклад Л.Эйлера в развитие математического анализа Леонард Эйлер (Euler, Leonhard) (1707–1783) входит в первую пятерку величайших математиков всех времен и народов. Родился в Базеле (Швейцария) 15 апреля ...
... динамике и соотношениям, которые связывают его с другими управляющими параметрами, характеризующими человеческое общество [7-10 ]. Можно установить непосредственную связь этого параметра с некоторой физической мерой, характеризующей как отдельного человека, так и человечество в целом, которая связывает этот биологический вид со всеми живыми и неживыми объектами природы – этой мерой является масса ...
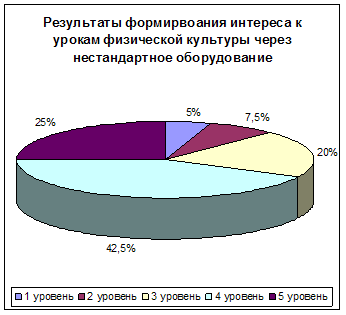
... у детей. Дети бережнее относится к инвентарю, повышается плотность урока, повышается качество обучения. Так же при использовании такого оборудования происходит влияние на формирование интереса младшего школьного возраста на уроках физической культуры. Происходит удовлетворение интереса, который может укрепляться, развиваться, становиться более глубоким и разносторонним. Интерес, таким образом, ...


0 комментариев