Всякое конечное множество является малым, всякое множество с конечным

6. Всякое конечное множество является малым, всякое множество с конечным

дополнением — большим. (При го­лосовании мнение конечного числа голосующих несущест­венно.)

Разбиение всех подмножеств натурального ряда на большие и малые, удовлетворяющее требованиям 1–6, называется нетривиальным ультрафильтром на множестве натуральных чисел.

Покажем теперь, что такое разбиение позволяет по­строить систему гипердействительных чисел, удовлетво­ряющую требованиям Основной гипотезы. Итак, пусть фиксировано разбиение, удовлетворяющее требованиям 1–6. Назовем две последовательности x_n и y_n эквивалентными, если множество тех n, при кото­рых x_n =y_n является большим. В силу требования 2 вся­кая последовательность эквивалентна самой себе.

Мы видим, что введенное отношение рефлексивно, сим­метрично (это очевидно из определения) и транзитивно и, следовательно, разбивает все последовательности действи­тельных чисел на классы эквивалентности, т. е. такие классы, что любые две последовательности одного класса эквивалентны, а любые две последовательности из разных классов – нет. Эти классы мы и назовем гипердействительными числами. Что еще нам нужно? Нужно, чтобы множество действительных чисел было подмножеством множества гипердействительных. Нужно уметь для каж­дой функции с действительными аргументами и значения­ми строить ее гипердействительный аналог. Нужно про­верить, что любая система уравнений и неравенств, гипердействительный аналог которой имеет гипердействительные решения, имеет действительные решения. И, на­конец, нужно убедиться, что среди гипердействительных чисел (рассматриваемых как упорядоченное поле) существуют бесконечно малые, отличные от нуля.

Чтобы сделать R подмножеством *R, отождествим каждое действительное число х с последовательностью х, х, х, ..., точнее, с содержащим ее классом. При этом разным действительным числам соответствуют разные классы: х,x,х … не эквивалентно у,у,y ... (множество тех n, при которых n-е члены совпадают, пусто и, следо­вательно, является малым).

Пусть f: R®R – функция с действительными аргу­ментами и значениями. Определим ее гипердействительный аналог *f: *R® *R. Пусть x – произвольное гипердействительное число, т.е. класс эквивалентных после­довательностей действительных чисел. Рассмотрим про­извольную последовательность x₀, x₁, x₂,… из этого класса и применим f ко всем ее членам. Класс, содержащий по­лученную последоваетльность f(x0), f(x1), f(x2), … и будем считать значением f на х. Полученный класс не зависит от выбора последовательности x₀, x₁, x₂,… в классе x (определение корректно).

Аналогично определяются и гипердействительные ана­логи для функций нескольких аргументов. Пусть, напри­мер, f – функция двух действительных аргументов с дей­ствительными значениями. Определим ее гипердействительный аналог *f. Чтобы применить *f к двум гипердействительным числам х и y, возьмем по­следовательности x₀, x₁, x₂,… и y₀, y₁, y₂,… , им принадлежа­щие, и в качестве *f(х, у) рассмотрим класс последова­тельности f(x0,y0), f(x1,y1), f(x2,y2),… Определение корректно.

Нужно проверить, что построенное гипердействительные аналоги будут продолжениями исходных функций с действительными аргументами и значениями. Это очевидно следует из определений. Проверим теперь, что вся­кая система уравнений и неравенств, имеющая гипердействительные решения, имеет и действительные решения. Пусть, на­пример, система

f(g(x,y),z)=z, h(x)¹h(y)

имеет гипердействительные решения x, y, z. Рассмотрим последовательности x0,x1,x2,…; y0,y1,y2,…; z0,z1,z2,…, при­надлежащие соответствующим классам эквивалентности. Тогда g(x0,y0), g(x1,y1),… принадлежит классу g(x,y), а f(g(x0,y0),z0), f(g(x1,y1),z1),… – классу f(g(x,y),z). Поскольку x,y,z по предположению являются решения­ми системы, то f(g(x_n,y_n),z_n)=z_n для большинства п. Поскольку h(x)¹h(y), последовательности h(x0),h(x1),… и h(y0),h(y1),… не эквивалентны и множе­ство тех п, при котором h(x_n)=h(y_n) малое. Тогда мно­жество тех п, при котором h(x_n)¹h(y_n) является боль­шим. Так как пересечение двух больших множеств является большим, то множество тех n, при котором

f(g(x_n,y_n),z_n)=z_n, h(x_n)¹h(y_n)

является большим. Значит, оно непусто. Таким образом, система имеет и действительные решения.

Осталось проверить, что среди гипердействительных чисел существуют бесконечно малые, отличные от нуля. Положительным бесконечно малым гипердействительным числом будет, например, класс последовательности 1, 1/2, 1/3, .,. (или любой другой последовательности положи­тельных действительных чисел, сходящейся к 0). Нам нужно проверить, что это гипердействительное число (обозначим его через e) положительно, но меньше любого стандартного положительного числа. Чтобы доказать это, мы должны вспомнить, как определяется порядок на мно­жестве гипердействительных чисел. Он определяется в со­ответствии с общей схемой построения гипердействительного аналога для любого отношения на множестве дей­ствительных чисел. Нужно взять функцию f двух дей­ствительных аргументов, для которой свойства f(x,y)=0 и х<у равносильны, и рассмотреть ее гипердействительный аналог *f. Гипердействительное число х называется меньшим гипердействительного числа у, если *f(x,y)=0. Посмотрим, что дает нам эта конструкция для построен­ной описанным способом системы гипердействительных чисел. Если х – класс последовательности x0,x1,x2,…, а y – класс последовательности y0,y1,y2,…, то *f(x,y) есть класс последовательности f(x0,y0), f(x1,y1), f(x2,y2), … Равенство этого класса нулю (т. е. классу последовательности 0, 0, 0, ...) означает, что f(xn,yn)=0 для большинства n, т. е. что xn<yn для большинства п. Таким образом, чтобы выяс­нить, верно ли х<у для гипердействительных чисел х и y, нужно взять последовательности x0,x1,x2,…, и y0,y1,y2,… в классах х и у и выяснить, является ли множество тех п, при которых xn<yn большим.

Нам нужно было проверить, что 0<e и что e<р для любого стандартного положительного р (e —класс последовательности 1, 1/2, 1/3, ...). Это просто:

0<e, так как 0<1/п при всех п (а множество N большое), e<р, так как 1/n<р для всех натураль­ных n, кроме конечного числа, а всякое множество с ко­нечным дополнением малое (свойство 6 “системы подсче­та голосов”). Отметим, что здесь мы впервые воспользо­вались свойством 6, до сих пор все наши рассуждения были справедливы и в случае “диктатуры” (когда боль­шими считаются те и только те множества, которые со­держат некоторое натуральное число N). В этом случае две последовательности эквивалентны, если совпадают их N-е члены, и все гипердействительные числа стандартны (класс последовательности x0,x1,x2,… совпадает со стан­дартным числом x_N).

1. Успенский В.А. Что такое нестандартный анализ? – М., Наука, 1987. – 128с.

2. Девис М. Прикладной нестандартный анализ. – М., Мир, 1980.

3. Успенский В.А. Нестандартный, или неархимедов, анализ. – М., Знание, 1983. 61 с. (Новое в жизни, науке, технике. Сер. “Математика, кибернетика” № 8 ).

4. Успенский В.А. Нестандартный анализ // Наука и жизнь, 1984. – №1. – с. 45-50.

5. Робинсон А. Введение в теорию моделей и математику алгебры. пер. с англ. – М., Наука, 1967.

Похожие работы

Спектр оператора. Применение нестандартного анализа для исследования резольвенты и спектра оператора

Скачать

36187

0

5

... состоит из значений функции g(x) на отрезке [a,b]. Причём этот оператор имеет лишь непрерывный спектр, так как резольвента при  существует, но не непрерывна. Точечного спектра оператор не имеет. Пример 3: Рассмотрим оператор дифференцирования на множестве дифференцируемых функций. А: (для краткости будем писать вместо f(x) просто f). Рассмотрим резольвенту этого оператора: , то есть мы должны ...

Вклад Л.Эйлера в развитие математического анализа

Скачать

31365

0

0

... «Математических лекциях о методе интеграла»[9]. Здесь дан способ взятия большинства элементарных интегралов и указаны методы решения многих дифференциальных уравнений первого порядка.   2 Вклад Л.Эйлера в развитие математического анализа   Леонард Эйлер (Euler, Leonhard) (1707–1783) входит в первую пятерку величайших математиков всех времен и народов. Родился в Базеле (Швейцария) 15 апреля ...

Человечество. Некоторые нестандартные модели

Скачать

36641

1

3

... динамике и соотношениям, которые связывают его с другими управляющими параметрами, характеризующими человеческое общество [7-10 ]. Можно установить непосредственную связь этого параметра с некоторой физической мерой, характеризующей как отдельного человека, так и человечество в целом, которая связывает этот биологический вид со всеми живыми и неживыми объектами природы – этой мерой является масса ...

Влияние использования нестандартного оборудования на формирование интереса младшего школьного возраста на уроках физической культуры

Скачать

69900

4

3

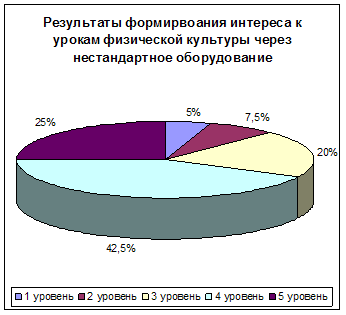
... у детей. Дети бережнее относится к инвентарю, повышается плотность урока, повышается качество обучения. Так же при использовании такого оборудования происходит влияние на формирование интереса младшего школьного возраста на уроках физической культуры. Происходит удовлетворение интереса, который может укрепляться, развиваться, становиться более глубоким и разносторонним. Интерес, таким образом, ...