Навигация
Общий курс высшей математики
Академия труда и социальных отношений
Курганский филиал
Социально-экономический факультет
КОНТРОЛЬНАЯ РАБОТА
по дисциплине: «Общий курс высшей математики»
Студент гр. ЗМб 1338
Ст. преподаватель
Курган – 2009
Задание 03
В ромбе ABCD известны координаты вершин А и С и тангенс внутреннего угла С. Найти уравнения диагоналей и сторон, координаты двух других вершин, а также площадь этого ромба, если А(4,2), С(16;18), ![]() . Сделать чертеж.
. Сделать чертеж.
Решение:
Зная координаты вершин А и С запишем уравнение диагонали АС как уравнение прямой, проходящей через две заданные точки:
![]()
![]()
12(y-2)=16(x-4);
12y-24=16х-64
16х-12у-40=0 /:4
4х-3у-10=0 – уравнение диагонали А С в форме общего уравнения прямой.
Перепишем это уравнение в форме уравнения прямой с угловым коэффициентом:
-3y=-10-4х;
3y=4x-10;
y=![]() откуда k А С=
откуда k А С=![]()
Так как в ромбе диагонали взаимно перпендикулярны, то угловой коэффициент диагонали BD будет равен
КВD = ![]()
![]()
Само же уравнение диагонали BD найдем как уравнение прямой, проходящей через заданную точку в направлении, определяемом угловым коэффициентом КBD.
В качестве «заданной точки» возьмем точку Е пересечения диагоналей ромба, которая лежит на середине отрезка АС, вследствие чего:
![]()
![]()
Е (10;10)
Итак, уравнение диагонали BD запишем в виде
у – yE= КВD(x-xE)
y-10=![]() (x-10);
(x-10);
y-10=![]() x+
x+![]() /
/![]() 4
4
4у-40=-3х+30
3х+4у-70=0 – уравнение диагонали BD
Чтобы найти уравнение сторон ромба, надо определить только угловые коэффициенты КАВ = КCD и КВС = КAD прямых, на которых эти стороны лежат, ибо точки, через которые эти прямые проходят, известны – это вершины А и С ромба.
Для определения указанных угловых коэффициентов воспользуемся формулой ![]() , позволяющей вычислять тангенс угла φ между двумя заданными прямыми по их угловым коэффициентам К1 и К2; при этом угол φ отсчитывается против часовой стрелки от прямой у = К1х + b1 до прямой у = К2х + b2. Формула оказывается удобной, потому что уравнение диагонали АС уже найдено (и, следовательно, известен ее угловой коэффициент КАС), а положение сторон ромба относительно этой диагонали однозначно определяется внутренними углами А и С, которые равны между собой и для которых по условию известен их тангенс (
, позволяющей вычислять тангенс угла φ между двумя заданными прямыми по их угловым коэффициентам К1 и К2; при этом угол φ отсчитывается против часовой стрелки от прямой у = К1х + b1 до прямой у = К2х + b2. Формула оказывается удобной, потому что уравнение диагонали АС уже найдено (и, следовательно, известен ее угловой коэффициент КАС), а положение сторон ромба относительно этой диагонали однозначно определяется внутренними углами А и С, которые равны между собой и для которых по условию известен их тангенс (![]() ).
).
Так диагонали ромба делят его углы пополам, то, положив ![]() из формулы
из формулы ![]() для тангенса двойного угла при
для тангенса двойного угла при ![]() найдем tg φ:
найдем tg φ:
![]()
Положим z = tg φ; тогда ![]() , тогда
, тогда
15 ![]() 2z = 8 (1-z2)
2z = 8 (1-z2)
30z=8-8z2
8z2+30z-8=0 /:2
4z2+15z-4=0
D=152-4![]() 4
4![]() (-4)= 225+64=289
(-4)= 225+64=289
z1=![]()
![]() ;
;
z2=![]()
![]()
Но т.к. угол в ромбе φ всегда острый корень z2=-4 отбрасываем и получаем в итоге, что tg φ =![]()
Угол φ является углом между прямыми ВС и АС, с одной стороны, и прямыми АС и CD – с другой (см. чертеж).
Потому в первом случае по формуле ![]() имеем
имеем ![]()
откуда при ![]() то получим
то получим
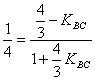
4(![]() )=1+
)=1+![]() ;
;
![]() =
=![]() /
/![]() 3
3
16-12 KBC=3+4KBC;
16 KBC=13;
KBC=![]()
Во втором случае по формуле ![]() имеем
имеем ![]() =
=![]() ;
;
При КАС =![]() получим:
получим:
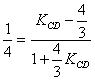 ;
;
4(KcD-![]() )=1+
)=1+![]() KcD;
KcD;
4KcD-![]() =1+
=1+![]() KcD /
KcD / ![]() 3;
3;
12KcD-16=3+4KcD;
8KcD =19
KcD= ![]()
Так как противоположные стороны ромба параллельны, то тем самым мы определили угловые коэффициенты всех его сторон.
КCD = KAB=![]() ;
;
KBC = KAD = ![]() .
.
Зная теперь эти угловые коэффициенты и координаты вершин А и С, по уже использовавшимся выше формулам найдем уравнения прямых АВ, CD, BC и AD.
Уравнение АВ: у – уA = KAB (х – хA),
у -2 = ![]() (х-4) /
(х-4) /![]() 8;
8;
8у-16=19х-76;
Похожие работы
бнику, решения задач необходимо ответить на вопросы для самопроверки, помещенные в конце темы. В соответствии с действующим учебным планом студенты-заочники изучают курс высшей математики в течение 1 и 2 семестра и выполняют в каждом семестре по две контрольные работы. Первая и вторая контрольные работы выполняются студентами в 1 семестре после изучения тем 1-2 и 3-4 соответственно. Третья и ...
... f ¢(xо) = 0, >0 (<0), то точка xоявляется точкой локального минимума (максимума) функции f(x). Если же =0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные. На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b]. Пример 3.22. Найти экстремумы функции f(x) ...
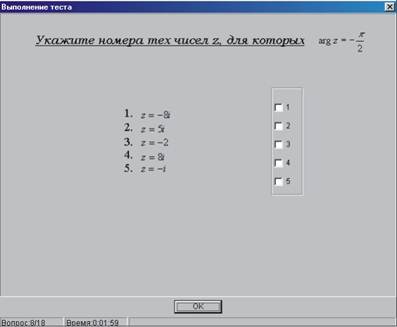
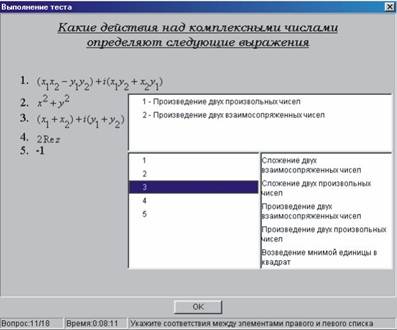
... , проводилось по всем темам учебного плана третьего семестра и носило исследовательский характер. Исследованию подлежали два основных пункта: Целесообразность использования данной тестирующей оболочки в процессе обучения высшей математике. Создание эффективных тестов, оценивающих умения учащихся. Необходимо было решить следующие диагностические задачи: сравнить уровни усвоения учебного ...
... функций. Следует помнить, что применять формулы (1.15), (1.16) или 1-6 можно для функции только в случае, если при . Упражнения к § 3.1 Комбинаторика 3.1 Вычислить: 3.2 Решить уравнения и неравенства: 1) 2) 3) 4) 5) 6) 7) 8) 3.3 Доказать: 1) , 2) 3) 4) 3.4 Сколько пятизначных чисел с неповторяющимися цифрами можно составить из пяти цифр ...


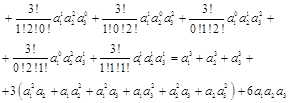
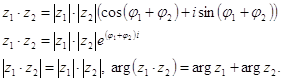
0 комментариев