Навигация
Основні поняття теорії ймовірностей
ОСНОВНІ ПОНЯТТЯ ТЕОРІЇ ЙМОВІРНОСТЕЙ
1. Предмет теорії ймовірностей
Теорія ймовірностей вивчає закономірності, властиві випадковим явищам. Як будь-яка математична наука, вона має аксіоматичну побудову, з якої виводяться подальші результати. Основні поняття теорії ймовірностей мають не абстрактний характер. Вони в загальній формі відображають певні сторони реальної дійсності. Тому висновки і результати, що одержують у теорії ймовірностей, мають практичну цінність.
Випадковим називається таке явище, характер протікання якого не можна цілком передбачити на підставі наявних у нас даних. Неможливість передбачення не означає відсутності причинного зв'язку між початковими даними і результатом. Вона викликана неповною поінформованістю про цей зв'язок. Проте неповнота даних не є перешкодою для з'ясування загальних закономірностей, що властиві випадковим явищам. Експериментатору добре відома така універсальна схема: чим більша кількість дослідів, тим більш впевнено можна вивести закономірність, тим меншою є роль випадкових відхилень.
Теорія ймовірностей вивчає масові випадкові явища, тобто явища, що допускають хоча б експериментальну перевірку в однотипних умовах необмежену кількість разів. При цьому розглядаються такі випадкові явища, об'єктивні характеристики яких можуть бути отримані з будь-яким рівнем точності за будь-яких необмежених повторень експерименту.
Під випробовуванням у теорії ймовірностей розуміється експеримент, що може бути повтореним при дотриманні визначеного комплексу умов необмежену кількість разів. У зв’язку з тим, що завдання комплексу умов не вичерпує всіх обставин, які впливають на результат експерименту, при повторенні іспиту може спостерігатися різний результат експерименту.
Наприклад, експеримент полягає у тому, що з урни, в якій є m білих і М чорних куль, навмання виймають одну кулю. Комплекс умов: склад куль за кольором; витаскування кулі навмання.
Експеримент може бути повторено безліч разів, якщо вийнята куля повертається назад. Даний експеримент можна назвати випробуванням.
При зміні комплексу заданих умов, що характеризують випробування, буде одержано нове випробування.
Для кожного випробування можна вказати деяку систему можливих наслідків, головна властивість яких полягає в тому, що в результаті випробування відбувається один і тільки один з цих наслідків. Така система наслідків, пов'язаних з даним випробуванням, називається простором елементарних подій W, а наслідки, що його складають, елементарними подіями w. Їх взаємозв’язок можна наочно зобразити схемою, наведеною на рис.
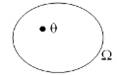
Рисунок 1
Приклад 1. Випробування - виймання кулі з урни, що містить m білих і M-m чорних куль, з її поверненням назад. Можливі елементарні події: w1 - витягнено білу кулю, w2 - витягнено чорну кулю; простір елементарних подій W= (w1, w2) складається тільки з двох подій.
Приклад 2. Іспит - постріли по мішені до першого влучення. Тепер простір елементарних подій W (w1,w2,…,wn…) складається з таких подій: wi - номер i-го влучення, w¥ - влучення не відбулося при нескінчених спробах. При цьому W - нескінченна безліч елементарних подій.
Приклад 3. Постріл по мішені з гарантованим влученням. Розміром кулі можна зневажити. Ставимо у відповідність кожній точці мішені q результат випробування w (q). W містить незліченну безліч елементарних подій.
2. Випадкова подія. Алгебра випадкових подій
Випадковою подією, пов’язаною з даним випробуванням, називається деяка множина елементарних подій, яка позначається прописними латинськими літерами (A, B, C,.). Тобто випадкова подія - це підпростір простору елементарних подій W. Про елементарні події, що входять до випадкової події, говорять, що вони їй сприяють. W обов'язково з'являється в результаті випробування, тому W називається достовірною подією.
Наприклад, якщо випробування полягає в одноразовому підкиданні гральної кості, то елементарними подіями є випадання на верхній грані цієї кості тієї чи іншої кількості очок. Тоді випадковими подіями можна вважати або одну з елементарних подій, або їх якесь об’єднання, як, наприклад, випадання парної кількості очок, кількості, що кратна трьом, випадання довільної кількості очок (W) тощо.
Приклад 4. В урні знаходяться дві білі і дві чорні кулі. Випробування полягає у вийманні навмання однієї кулі з урни. Занумеруємо кулі і позначимо елементарні події, що полягають у вийманні білої кулі під номером 1 через w1, білої кулі під номером 2 - w2, так само чорної кулі під номером 3 - w3, чорної кулі під номером 4 - w4. W = (w1, w2, w3, w4). Тоді подія А (w1, w3) полягає у вийманні з урни кулі з непарним номером, подія В (w1,w2) - це виймання білої кулі.
Наочно випадкові події можна геометрично зобразити підмножинами простору елементарних подій W, як це продемонстровано на рис.2.
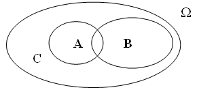
Рисунок 2
Алгебра випадкових подій (у межах того самого простору W):
Похожие работы
... аксіоматичного визначення поняття ймовірності П.Л. Чебишев (1821–1894 р.) був творцем і ідейним керівником петербурзької математичної школи. Чебишев зіграв велику роль у розвитку багатьох розділів математики, у тому числі теорії ймовірностей. У своїй магістерській дисертації в першому розділі він уводить поняття ймовірності. Для цього він, насамперед, визначає рівно можливі події: «Якщо з ...
... . Поклавши у формулі (4) а = b = 1, дістанемо Нехай маємо скінченну множину, яка містить п елементів. Тоді кількість підмножин цієї множини дорівнює 2n. Наприклад, для множини {a,b,c} маємо Ø, {a}, {b}, {c}, {a,b}, {a,c}, {b,c}, {a,b,c}. ПОЧАТКИ ТЕОРІЇ ЙМОВІРНОСТЕЙ § 1. Про предмет теорії ймовірностей До цього часу розглядалися задачі, в яких результат дії був однозначно ...
... у рішенні. Точність як би здатна виникати нізвідки, і це міцно осідає в підсвідомості учнів. Приведу тільки один приклад з добротного у всіх інших відносинах "Керівництва до рішення задач по теорії ймовірностей і математичній статистиці" В. Е. Гмурмана. Імовірність появи події в кожнім з 100 незалежних іспитів постійна і дорівнює р=0,8. Знайти імовірність того, що подія з'явиться не менш 75 разів ...
... Метод моментів Метод моментів є одним із методів точечного оцінювання параметрів розподілу. Нехай закон розподілу випадкової величини X відомий із точністю до числових значень його параметрів 1,2,…,k. Це означає, що відомий вид функції щільності fx(х, ), де = (1,2,…,k), якщо X безперервна (відомий вид функції ймовірності Р (X= х,), якщо X дискретна), але числові значення k параметрів не відомі. ...


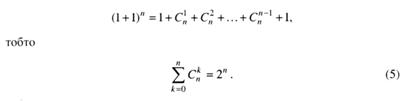


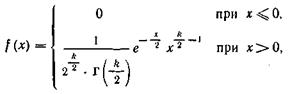
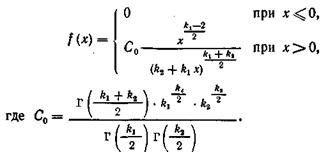

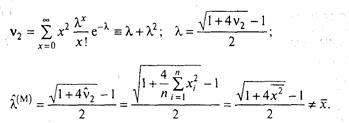
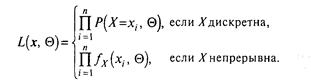
0 комментариев