Навигация
Для будь-якої якої події А та для будь-якої серії випробувань
1. Для будь-якої якої події А та для будь-якої серії випробувань
0£p* (A) £
2. Частота появи достовірної події ![]()
3. Якщо події А і В несумісні, то:
![]()
Дійсно, нехай під час проведення n випробувань отримано mAпояв події А і mB появ події В, тоді mA+mB - кількість появи події А+В. Отже:
![]()
Якщо А і В - сумісні, то
![]() ,
,
тому що (рис.10)
![]()
Це наочно видно також на схемі рис.10.

Рисунок 10
Поняття частоти є основним при експериментальному вивченні випадкових подій. Однак частота не може бути об'єктивною характеристикою випадкової події, що досліджується. Вона залежить від випадкового збігу обставин, пов'язаних з даною серією випробувань, від індивідуальних особливостей самого дослідника. Проте експериментально встановлено, що зі зростанням чисельності випробувань частота стає майже сталою.
Ймовірність випадкової події відповідає в ідеалізованому вигляді тій сталій межі, до якої тяжіє частота випадкової події при необмеженому збільшенні чисельності випробувань.
Теорія ймовірностей призначена для опису випадкових подій, що мають сталу (стійку) частоту.
4. Розібрані вправиЗ безлічі подружніх пар навмання вибирається одна пара. Подія А: "чоловіку більше 30 років", подія В: "чоловік старше дружини", подія С: "дружині більше 30 років".
а) З'ясувати, в чому полягають події АВС, А-АВ, ![]() .
.
б) Перевірити, що ![]() .
.
Відповідь: а) АВС - "обидва: і чоловік, і дружина - старше 30 років, причому чоловік старше дружини"; А-АВ - "чоловіку більше 30 років, але він не старше своєї дружини"; ![]() - "обидва: і чоловік, і дружина - старше 30 років, причому чоловік не старше своєї дружини";
- "обидва: і чоловік, і дружина - старше 30 років, причому чоловік не старше своєї дружини";
б) ![]() - "чоловіку більше 30 років" і "дружині не більше 30 років", отже чоловік старше дружини - В, тобто
- "чоловіку більше 30 років" і "дружині не більше 30 років", отже чоловік старше дружини - В, тобто![]() .
.
2. Нехай А, В, С - три довільних події. Визначити подію, що полягає в тому, що з А, В, С
а) відбулося тільки А;
б) відбулися тільки А та В;
в) усі три події відбулися;
г) відбулася принаймні одна з подій;
д) відбулися принаймні дві події;
е) відбулася одна і тільки одна подія;
ж) відбулися дві і тільки дві події;
з) жодна подія не відбулася;
і) відбулося не більше двох подій.
Відповідь:
![]()
ж) ![]()
3. Нехай А та В - довільні події, U - достовірна подія, а V - неможлива подія. Довести, що А, ![]() ,
, ![]() , U, V утворять повну групу подій.
, U, V утворять повну групу подій.
Відповідь: Легко перевірити, що перші три події попарно несумісні, сума їх дорівнює U.
4. У чому полягає умова сумісності подій А+В, ![]() і
і ![]() ?
?
Відповідь: З того, що (А+В) (![]() , випливає необхідність сумісності А і В.
, випливає необхідність сумісності А і В.
5. Довести, що подія (А+В) (![]() є неможливою.
є неможливою.
6. Чи є рівносильними події А і В, якщо
а) ![]()
б) А+С=В+С?
в) АС=ВС?
Відповідь: а) так; б) взагалі кажучи, необов’язково в) взагалі кажучи, необов’язково.
7. Нехай А, В, С - довільні події. Спростити дані вирази для подій:
а) (А+В) (В+С);
б) (А+В) (А+![]() ).
).
Відповідь:
а) (А+В) (В+С) =АВ+АС+ВВ+ВС= (А+В+С) В+АС=В+АС;
б) (А+В) (А+![]() ) = АА+АВ+А
) = АА+АВ+А![]() +В
+В![]() =А+А (В+
=А+А (В+![]() ) +
) +![]() = А+АW+
= А+АW+![]() =А.
=А.
Похожие работы
... аксіоматичного визначення поняття ймовірності П.Л. Чебишев (1821–1894 р.) був творцем і ідейним керівником петербурзької математичної школи. Чебишев зіграв велику роль у розвитку багатьох розділів математики, у тому числі теорії ймовірностей. У своїй магістерській дисертації в першому розділі він уводить поняття ймовірності. Для цього він, насамперед, визначає рівно можливі події: «Якщо з ...
... . Поклавши у формулі (4) а = b = 1, дістанемо Нехай маємо скінченну множину, яка містить п елементів. Тоді кількість підмножин цієї множини дорівнює 2n. Наприклад, для множини {a,b,c} маємо Ø, {a}, {b}, {c}, {a,b}, {a,c}, {b,c}, {a,b,c}. ПОЧАТКИ ТЕОРІЇ ЙМОВІРНОСТЕЙ § 1. Про предмет теорії ймовірностей До цього часу розглядалися задачі, в яких результат дії був однозначно ...
... у рішенні. Точність як би здатна виникати нізвідки, і це міцно осідає в підсвідомості учнів. Приведу тільки один приклад з добротного у всіх інших відносинах "Керівництва до рішення задач по теорії ймовірностей і математичній статистиці" В. Е. Гмурмана. Імовірність появи події в кожнім з 100 незалежних іспитів постійна і дорівнює р=0,8. Знайти імовірність того, що подія з'явиться не менш 75 разів ...
... Метод моментів Метод моментів є одним із методів точечного оцінювання параметрів розподілу. Нехай закон розподілу випадкової величини X відомий із точністю до числових значень його параметрів 1,2,…,k. Це означає, що відомий вид функції щільності fx(х, ), де = (1,2,…,k), якщо X безперервна (відомий вид функції ймовірності Р (X= х,), якщо X дискретна), але числові значення k параметрів не відомі. ...


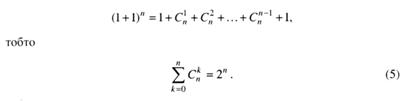


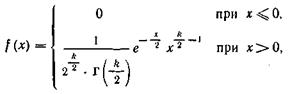
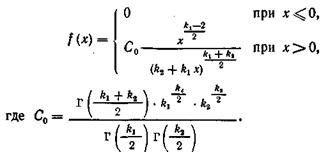

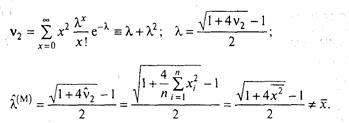
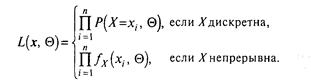
0 комментариев