Навигация
Дві події називаються рівносильними (тотожними), якщо вони складаються з одних і тих самих елементарних подій (А=В)
1. Дві події називаються рівносильними (тотожними), якщо вони складаються з одних і тих самих елементарних подій (А=В).
2. Подія В називається наслідком події А, якщо з появи події А випливає поява В. Цей взаємозв’язок символічно позначають так: АÌВ (рис.3).
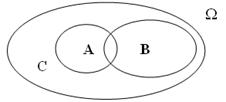
Рисунок 3
Якщо АÌВ; ВÌА, то А=В; також, якщо АÌВ і ВÌС; то АÌС.
3. Подією, протилежною події А (позначається як ![]() ), називається подія, рівносильна тому, що подія А не з’явиться (рис.4).
), називається подія, рівносильна тому, що подія А не з’явиться (рис.4).
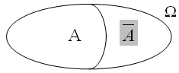
Рисунок 4
Очевидно, що ![]() = А; якщо AÌB; то
= А; якщо AÌB; то ![]() .
.
4. ![]() - неможлива подія - "порожня множина"
- неможлива подія - "порожня множина" ![]() ÌА.
ÌА.
5. Сумою двох подій А та В називається подія (вона позначається як А + В, або АÈВ), яка полягає в тому, що в результаті випробування відбудеться принаймні одна з подій А чи В (рис.5).
6. Добутком подій А та В (їх перетином) називається подія (вона позначається як А×В, або АÇВ), що складається з елементарних подій, сприятливих і А, і В, тобто вона полягає в тому, що в результаті випробування одночасно відбуваються обидві ці події (рис.6).
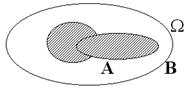
Рисунок 5

Рисунок 6
Поняття суми та добутку подій можна поширити на будь-яку кількість подій, як скінчену, так і нескінчену.
7. Події А і В називаються несумісними, якщо вони не можуть з'явитися в одному й тому самому випробуванні. АВ=![]() (рис.7).
(рис.7).
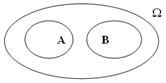
Рисунок 7
Події називаються попарно несумісними, якщо будь-які дві з них є несумісними. Події А1, А2,, …, Аn, складають повну групу, якщо вони попарно несумісні, а їх сума дає достовірну подію. Геометрично область W поділяється на області А1, А2,, …, Аn, що не мають попарно загальних точок перетину (рис.8).
теорія ймовірностей випадкова подія
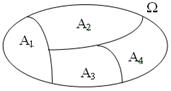
Рисунок 8
Основні формули алгебри випадкових подій:
1. Комутативність суми та добутку: А + В= В +А; А × В= В ×А.
2. Асоціативність суми та добутку: А + (В+С) = (А+ В) +С; А× (В×С) = (А×В) ×С.
3. А×В<A<A+B.
4. АÌ ВÞА+В=В, АВ=А, А+ W=W; А×W=А; А+![]() =А; А
=А; А![]() =
=![]() ; А+А=А; А×А=А.
; А+А=А; А×А=А.
5. Дистрибутивність множення відносно додавання
(А+В) С=АС+ВС; В .
.
6. Дистрибутивність додавання відносно множення
(А×В) +С= (А+С) × (В+С).
7. Властивості протилежних подій: при переході до протилежних подій сума заміняється добутком і навпаки:
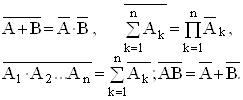
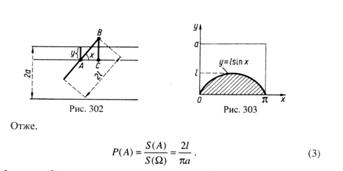
Приклад 5. Якщо електричне коло має два контакти, що з'єднані паралельно (випадок а)) і послідовно (випадок б)) (рис.9), тоді простір елементарних подій W= (w1,w2,w3,w4) складається з таких елементарних подій: w1 - обидва контакти замкнено; w2 - обидва контакти розімкнено; w3 - 1 - замкнено; 2 - розімкнено; w4 - 1 - розімкнено; 2 - замкнено.
Рисунок 9
Позначимо події: А - 1 контакт замкнено; В-2 контакт замкнено; С - все коло замкнено.
Тоді справедливі такі твердження:
А=w1+w3; В=w1+w4,а також
С=А+В; ![]()
у випадку а) і
C=AB; ![]()
у випадку б).
3. Частота і ймовірність випадкової подіїЧастота - це кількісна характеристика випадкових подій.
Нехай у серії з n випробувань m разів з'являється подія А: 0£m£ n. Число m називається частотою появи події А, а відношення ![]() називається питомою (нормованою) частотою появи події А у цій серії випробувань і позначається:
називається питомою (нормованою) частотою появи події А у цій серії випробувань і позначається:
![]() . (1)
. (1)
Питома частота має такі властивості:
Похожие работы
... аксіоматичного визначення поняття ймовірності П.Л. Чебишев (1821–1894 р.) був творцем і ідейним керівником петербурзької математичної школи. Чебишев зіграв велику роль у розвитку багатьох розділів математики, у тому числі теорії ймовірностей. У своїй магістерській дисертації в першому розділі він уводить поняття ймовірності. Для цього він, насамперед, визначає рівно можливі події: «Якщо з ...
... . Поклавши у формулі (4) а = b = 1, дістанемо Нехай маємо скінченну множину, яка містить п елементів. Тоді кількість підмножин цієї множини дорівнює 2n. Наприклад, для множини {a,b,c} маємо Ø, {a}, {b}, {c}, {a,b}, {a,c}, {b,c}, {a,b,c}. ПОЧАТКИ ТЕОРІЇ ЙМОВІРНОСТЕЙ § 1. Про предмет теорії ймовірностей До цього часу розглядалися задачі, в яких результат дії був однозначно ...
... у рішенні. Точність як би здатна виникати нізвідки, і це міцно осідає в підсвідомості учнів. Приведу тільки один приклад з добротного у всіх інших відносинах "Керівництва до рішення задач по теорії ймовірностей і математичній статистиці" В. Е. Гмурмана. Імовірність появи події в кожнім з 100 незалежних іспитів постійна і дорівнює р=0,8. Знайти імовірність того, що подія з'явиться не менш 75 разів ...
... Метод моментів Метод моментів є одним із методів точечного оцінювання параметрів розподілу. Нехай закон розподілу випадкової величини X відомий із точністю до числових значень його параметрів 1,2,…,k. Це означає, що відомий вид функції щільності fx(х, ), де = (1,2,…,k), якщо X безперервна (відомий вид функції ймовірності Р (X= х,), якщо X дискретна), але числові значення k параметрів не відомі. ...


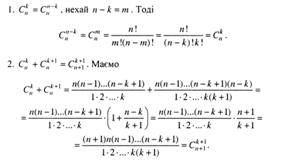
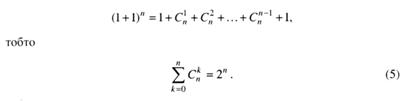


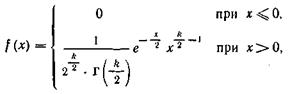
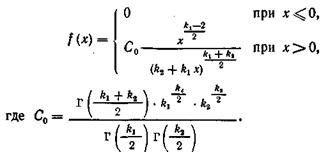

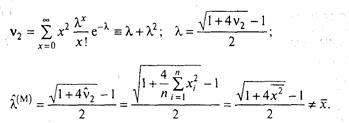
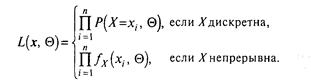
0 комментариев