Навигация
Подання різних функцій через гіпергеометричну
2. Подання різних функцій через гіпергеометричну
Гіпергеометрична функція F(![]() ,
, ![]() ,
, ![]() ,z) приводиться до полінома, коли
,z) приводиться до полінома, коли ![]() =0,-1,-2,…або
=0,-1,-2,…або ![]() =0,-1,-2. Наприклад,
=0,-1,-2. Наприклад,
F(![]() , 0,
, 0, ![]() ,z)=
,z)= ![]()
![]() zk=
zk=![]() =1,
=1,
тому що
![]() =0(0+1)(0+2)…....(0+k-1)=0.
=0(0+1)(0+2)…....(0+k-1)=0.
F(![]() , -2,
, -2, ![]() ,z)=
,z)= ![]()
![]() zk=
zk=![]() z0+
z0+![]() z+
z+![]() z2 =
z2 =
=1-2![]() z+
z+![]() z2,
z2,
тому що
![]() =1,
=1, ![]() =-2,
=-2,
![]() =(-2)(-1)=2,
=(-2)(-1)=2, ![]() =(-2)(-1)0=0,
=(-2)(-1)0=0, ![]() =(-2)(-1)01=0
=(-2)(-1)01=0
і так далі.
Перетворення
F(![]() ,
, ![]() ,
, ![]() ,z)=(1-z
,z)=(1-z![]() F(
F(![]() -
-![]() ,
,![]() -
-![]() ,
, ![]() ,z)
,z)
![]() -
-![]() =0
=0![]()
![]() =
=![]()
показує, що гіпергеометрична функція при ![]() -
-![]() =0,-1,-2,…або
=0,-1,-2,…або ![]() -
-![]() =0,-1,-2,…виражається через алгебраїчні функції. Зокрема,
=0,-1,-2,…виражається через алгебраїчні функції. Зокрема,
F(![]() ,
, ![]() ,
, ![]() ,z)= (1-z
,z)= (1-z![]() ,
, ![]() (3.1)
(3.1)
Надаючи параметрам ![]() ,
, ![]() спеціальні значення, знаходимо
спеціальні значення, знаходимо
(1-z)v= F(-v, 1, 1,z)
(1-z![]() = F(
= F(![]() , 1, 1,z (3.2)
, 1, 1,z (3.2)
(1-z)n= F(-n, ![]() ,
, ![]() ,z)
,z)
n=0,1,2,...
Щоб одержати подання логарифмічної функції, скористаємося розкладанням
ln(1-z)= - ![]()
![]() =-z
=-z![]()
![]()
![]() <1
<1
звідки треба
ln(1-z)=-zF(1,1,2,z) ![]() (3.3)
(3.3)
Аналогічним образом виводяться формули для зворотних кругових функцій:
arctg z=zF(![]() ,1,
,1, ![]() ,-z2)
,-z2) ![]() (3.4)
(3.4)
arcsin z=zF(![]() ,
,![]() ,
, ![]() ,z2)
,z2) ![]()
arctg z=![]() (-1)k
(-1)k![]() =z
=z![]()
![]() =z
=z![]()
![]() =
=
=z![]()
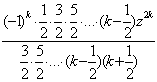 =z
=z ![]()
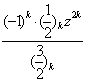 =z
=z![]()
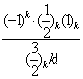 =zF(
=zF(![]() ,1,
,1, ![]() ,-z2),
,-z2),
тому що ![]() =1*2*…*k=k!
=1*2*…*k=k!
arcsinz=z+![]()
![]() =z[1+
=z[1+![]()
![]() ]=
]=
=z[1+![]()
![]() ]=z[1+
]=z[1+![]()
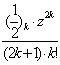 ]=z[1+
]=z[1+![]()
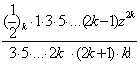 ]=
]=
=z[1+![]()
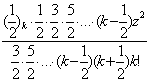 ]=z[1+
]=z[1+![]()
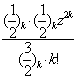 =zF(
=zF(![]() ,
,![]() ,
,![]() ,z2)...
,z2)...
Похожие работы
... з арифметики: відшукати суму деякої кількості натуральних послідовних чисел. Учитель вважав, що учні досить довго шукатимуть відповідь. Але через кілька хвилин Карл розв'язав задачу. Коли вчитель проглянув розв'язання, то побачив, що малий Гаусс винайшов спосіб скороченого знаходження суми членів арифметичної прогресії. Щасливий випадок звів Гаусса з першим у навчанні учнем цієї самої школи – ...

0 комментариев