Навигация
1. Допущения
При решении задачи о чистом кручении стержней следуют "полуобратному методу" Сен-Венана, полагая
где z - ось стержня.
2. Основные уравнения
При принятых допущениях расчетные уравнения будут:
Статистические уравнения
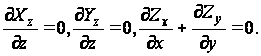(85)
Краевые условия
на боковой поверхности
(86)
на торцах (z=0 и z=l)
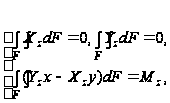(87)
где Mz крутящий момент.
Геометрические уравнения
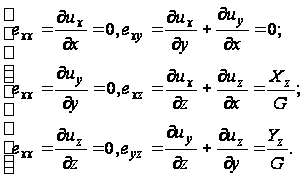(88)
(89)
3. Решение задачи посредством функции Прандля
Напряжения
выражают через
функцию 
по формулам:
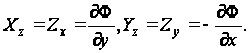(90)
Согласно уравнениям (89)
(91)
Интегрированием уравнений (88) находят, отбросив члены, представляющие перемещение стержня как твёрдого тела:
(92)
где 
угол закручивания
на единицу
длины стержня.
Из двух последних уравнений (88) получают уравнение
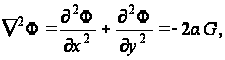
откуда
(93)
4. Свойства функции Прандля
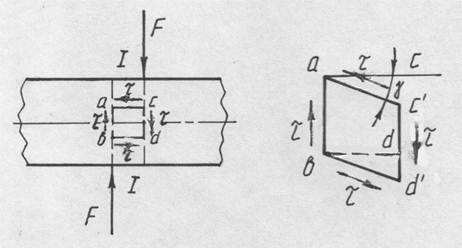
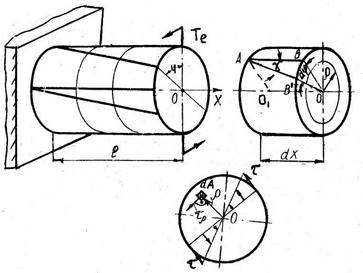
Из уравнения (86) (рис.18)
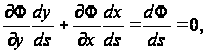
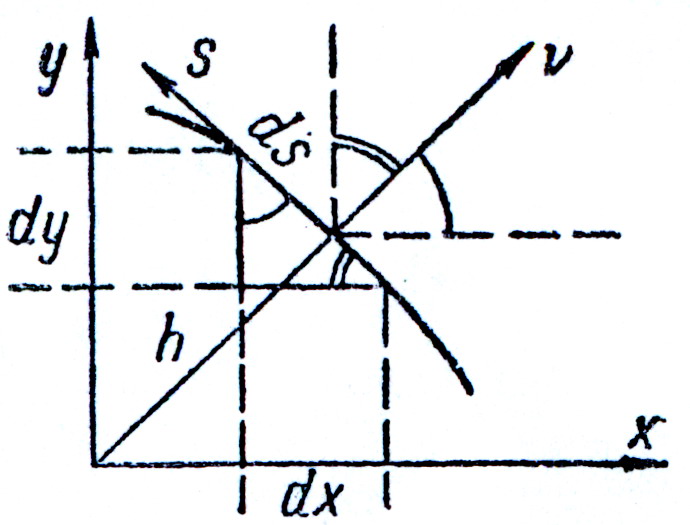
рис.18
и, следовательно, на контуре сплошного стержня
(94)
Касательное
напряжение
в любой точке
сечения направлено
по касательной
к линии 
,
проходящей
через эту точку,
и пропорционально
быстроте изменения 
по нормали к
этой линии:
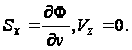(95)
Согласно теореме о циркуляции касательного напряжения (Бредт, 1896 г.)
(96)
где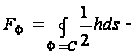 
площадь сплошного
сечения, ограниченная
рассматриваемой
кривой.
Согласно третьему уравнению (87)
(97)
где 
дифференциал
функции напряжений
(95); F
- площадь сечения
(включая отверстия).
§3.2 Чистое кручение круглых стержней (валов) переменного сечения
Похожие работы
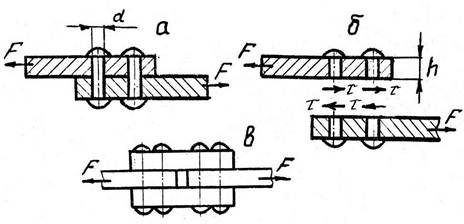
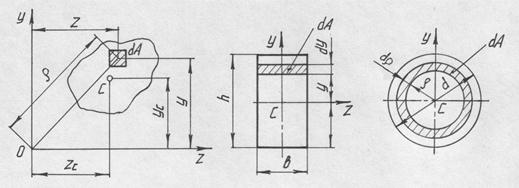
... будут соответственно обозначать диаметр болтов и допускаемое напряжение материала болтов на сдвиг (срез). ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ При рассмотрении деформации растяжения, сжатия, сдвига было установлено, что прочность и жесткость элементов конструкций зависит только от величины поперечного сечения и свойств материала элементов. При деформациях кручения и изгиба, при ...
... сечения увеличиваются. Из-за трения между опорными плитами нагружающего устройства и торцевыми поверхностями образца он принимает бочкообразную форму. Для ряда пластичных материалов обнаружить напряжение, аналогичное временному сопротивлению при растяжении, не удается, так как образец сплющивается. Хрупкие материалы проявляют значительно лучшую способность сопротивляться деформациям сжатия, чем ...
... ребрами) изображают конструктивные и потоковые функциональные структуры [14]. Принципы построения функциональных структур технических объектов рассматриваются в последующих главах курса "Основы проектирования им конструирования" не включенных в настоящее пособие. Для систем управления существуют характеристики, которые можно использовать в качестве критериев для оценки структур. Одна из них - ...
... Из выражений (4) и (5) можно найти значение осевого момента сопротивления W поперечного сечения вала как или и далее величину диаметра вала . Местные напряжения Напряжения при растяжении (сжатии), изгибе, кручении и сложных деформациях, определяемые по рассмотренным выше зависимостям, называют расчетными или номинальными. Экспериментально установлено, что в местах приложения сил, в местах ...
0 комментариев