Допущения

1. Допущения

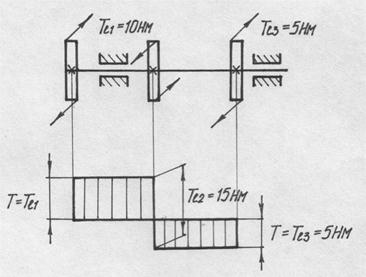
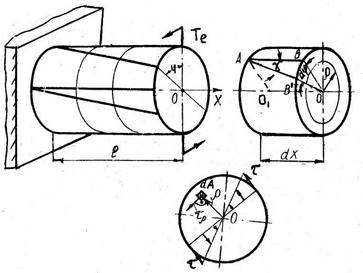
При кручении вала переменного сечения (рис. 19) задача решается

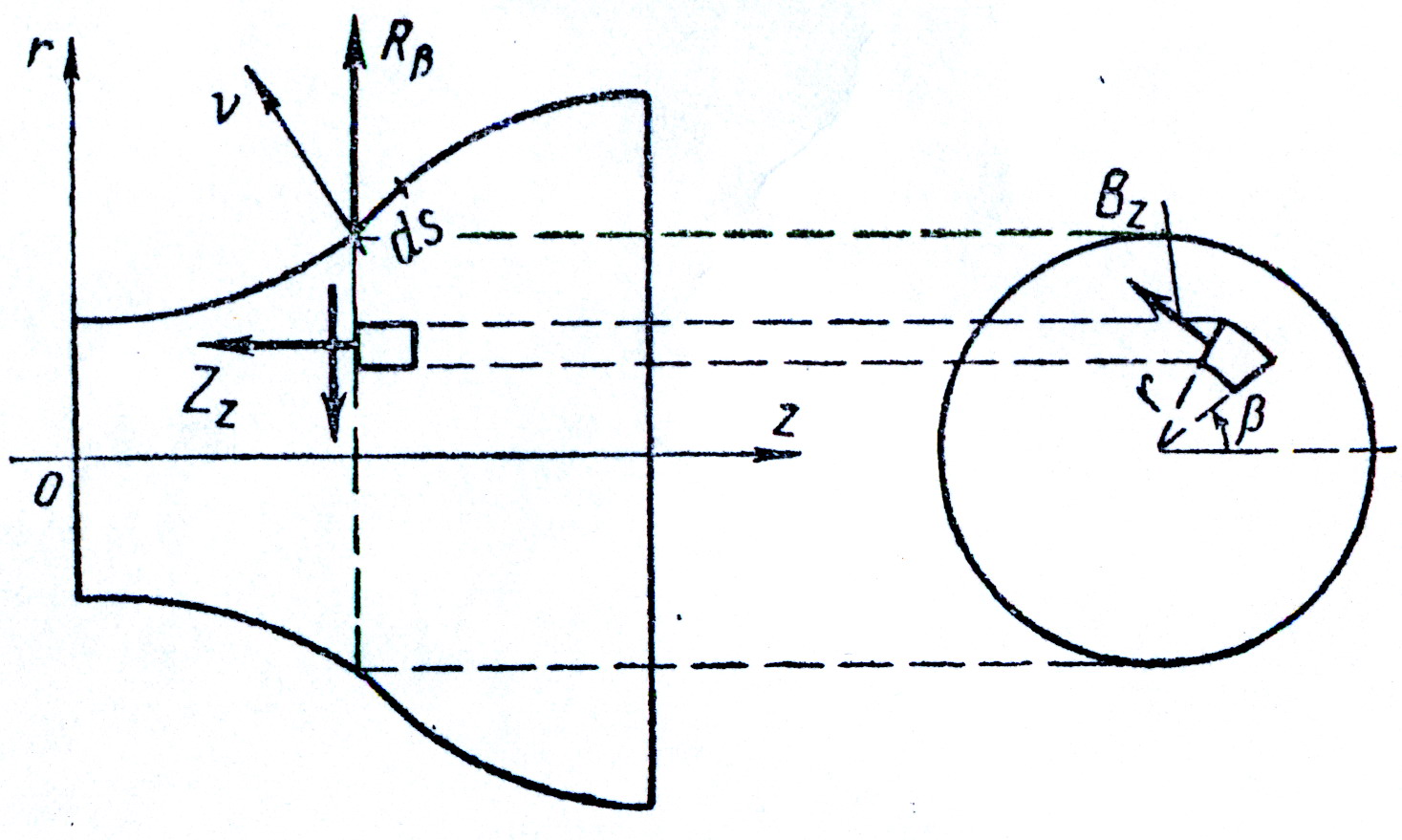
рис.19

в цилиндрических координатах при следующих допущениях:

(98)

2. Основные уравнения

При принятых допущениях (98) расчетные уравнения будут:

Геометрическое уравнение

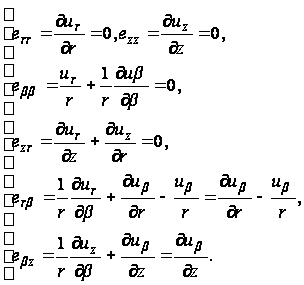(99)

Уравнения закона Гука

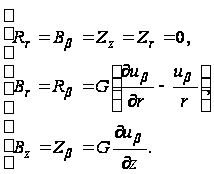(100)

Статические уравнения

При отсутствии объемных сил из уравнений равновесия остается лишь одно:

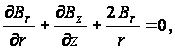
а остальное удовлетворяются тождественно.

Последнее уравнение можно записать в форме:

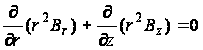(101)

и тождественно удовлетворить введением функции напряжений по формулам:

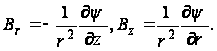(102)

Решая совместно уравнения (100) и (102) получаем:

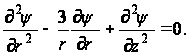(103)

Если боковая поверхность свободна от внешних сил, то результирующее касательное напряжение направлено по касательной к контуру осевого сечения, а его проекция на нормаль v равна нулю. В этом случае имеем:

Где

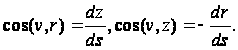
Приняв во внимание формулы (92), получим:

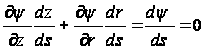
откуда следует, что на контуре

(104)

на торцах (z=0 и z=l)

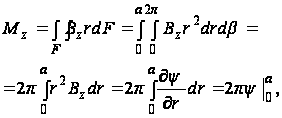(105)

где a - радиус рассматриваемого поперечного сечения, определяемый уравнением образующей.

Если на боковой поверхности действует нагрузка p, то

,

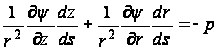Откуда

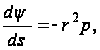
и вместо формулы (104) получим:

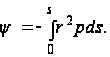(106)

3. Решение дифференциального уравнения кручения вала

Возможны различные формы решений уравнения (103)

В степенных функциях.

Полагаем

(107)

Подставляя значение в уравнение (103), находим n=4 и m=1, откуда

(108)

и напряжения принимают вид:

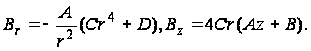(109)

Из формул (109) получаем ряд частных случаев, например при A=D=0 и B=1 - элементарное решение задачи о кручении круглого вала. В этом случае

и на основании формулы (105)

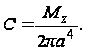
В функциях Бесселя.

Полагая

где R(r) - функция переменной r, а Z(z) - переменной z, и подставляя в уравнение (103), получаем:

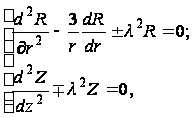(110)

где некоторое число.

Уравнения (110) имеют следующие два решения:

(111)

(112)

где,

функция Бесселя второго порядка действительного аргумента соответственно первого и второго рода;

функция Бесселя второго порядка мнимого аргумента соответственно первого и второго рода.

Напряжения определяют по формулам:

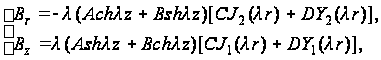(113)

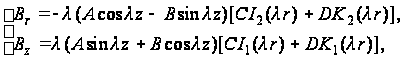И (114)

где J1, Y1, I1, K1 - функция Бесселя первого порядка.

В функциях Лежандра.

Дифференциальное уравнение кручения валов переменного сечения (103) в криволинейных, ортогональных, изотермических координатах имеет вид:

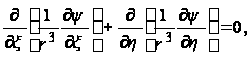(115)

где криволинейные, ортогональные, изотермические координаты в плоскости осевого сечения вала.

Координаты в плоскости (см. рис.19) связаны с координатами r и z соотношениями:

(116)

и обратно

Полагая

где функция , а функция , и подставляя в уравнение (115), получаем, учтя формулы (116), два уравнения:

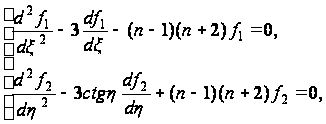(117)

где n- некоторое постоянное число.

Из первого уравнения (117), принимая , находим:

(118)

Решение второго уравнения (117) ищем в форме:

(119)

где

Подставляя значение во второе уравнение (117), приходим к уравнению Лежандра:

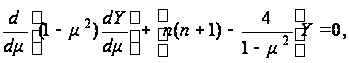(120)

откуда

(121)

где функции Лежандра первого рода, а при n – целом числе – полиномы Лежандра.

Первое решение уравнения (115) будет

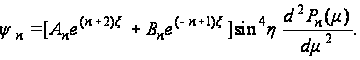(122)

Второе решение имеет вид:

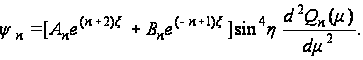(123)

где функция Лежандра второго рода.

При n=0 и n=1 решения получаются непосредственно из второго уравнения (117):

при n=0

при n=1

Таким образом, решения (122) и (123) дополняются двумя значениями функции :

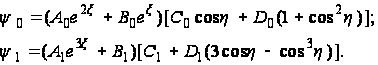(124)

При эллиптических координатах , которые связаны с координатами r и z соотношениями:

(125)

Полагая

приходим к решению в форме:

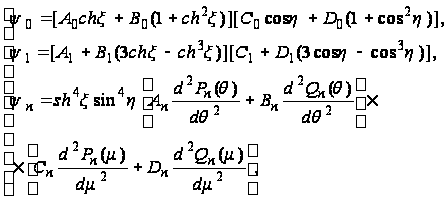(126)

где

Pn(…) - функция Лежандра первого рода;

Qn(…) – функция Лежандра второго рода.

Если переменить роли координат r и z, т.е. расположить полюса эллиптической системы координат не на оси вала Oz, а на оси Or, то связь между r, z и будет

(127)

и решение (126) примет вид:

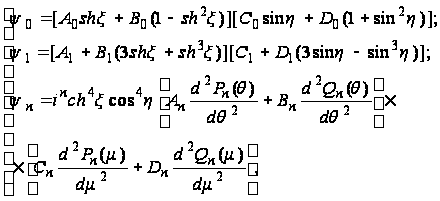(128)

где

ГЛАВА 4. ЗАДАЧИ

1. Стержень эллиптического сечения 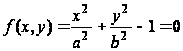скручивается моментом Mz.

Исследовать напряженное состояние стержня.

Задаемся функцией напряжений в виде:

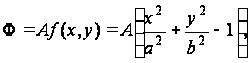(a)

где A-неизвестный множитель.

Подставляя функцию Ф в уравнение (91), получаем:

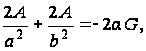
Откуда

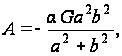
и функция напряжений

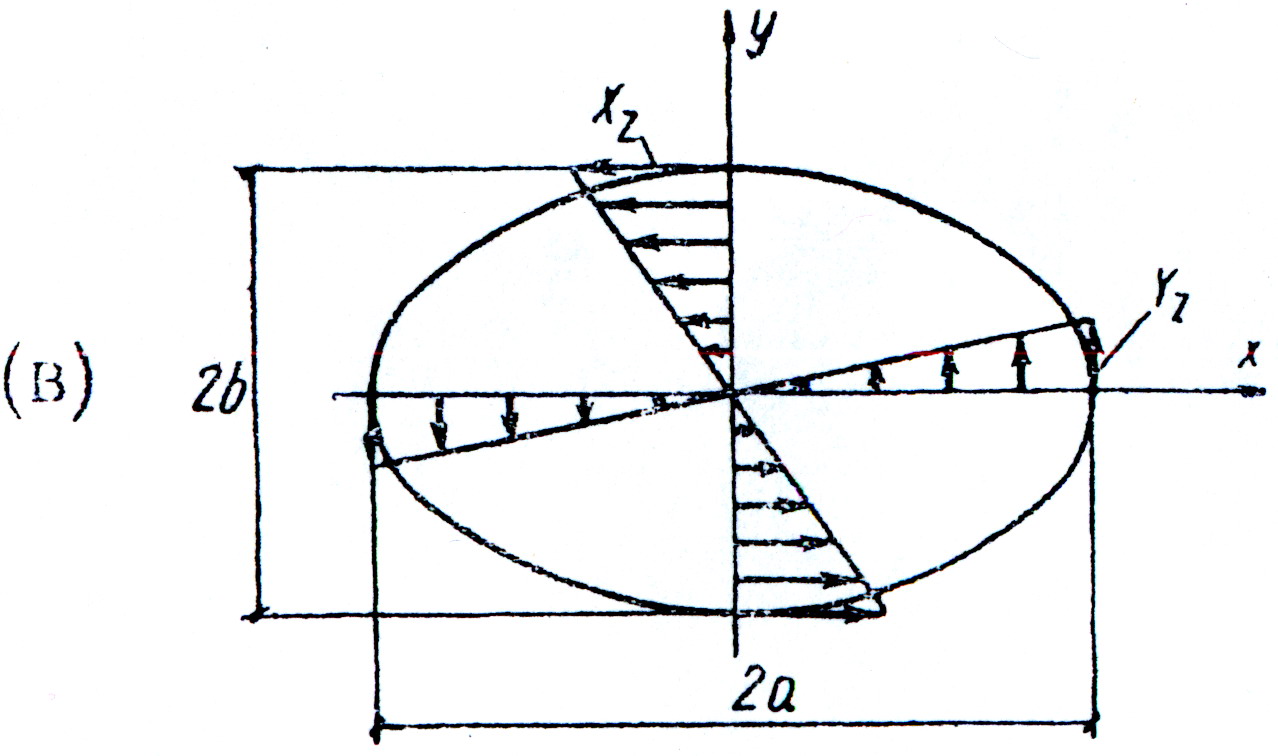
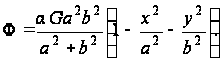(б)

Напряжения определяем по формулам (90):

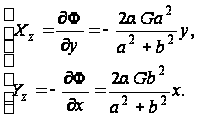(в)

Эпюры напряжений приведены на рис.20. рис.20

Для определения пользуемся формулой (97).

Согласно формуле (б) площадь эллипса

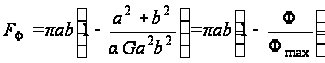
где при x=y=0

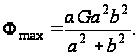
По формуле (97)

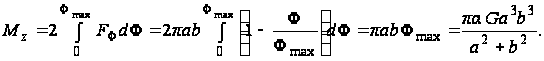
Наибольшее напряжение в точке (0, b)

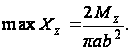
Похожие работы

Деформация сдвига. Геометрические характеристики плоских сечений. Кручение стержней с круглым поперечным сечением

Скачать

20350

0

5

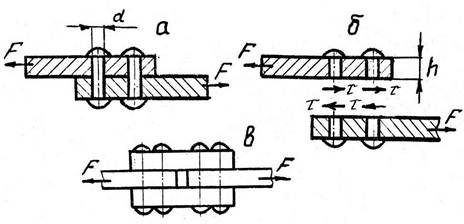
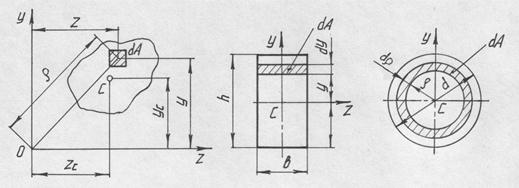
... будут соответственно обозначать диаметр болтов и допускаемое напряжение материала болтов на сдвиг (срез).   ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ При рассмотрении деформации растяжения, сжатия, сдвига было установлено, что прочность и жесткость элементов конструкций зависит только от величины поперечного сечения и свойств материала элементов. При деформациях кручения и изгиба, при ...

Сопротивление материалов

Скачать

85824

1

44

... сечения увеличиваются. Из-за трения между опорными плитами нагружающего устройства и торцевыми поверхностями образца он принимает бочкообразную форму. Для ряда пластичных материалов обнаружить напряжение, аналогичное временному сопротивлению при растяжении, не удается, так как образец сплющивается. Хрупкие материалы проявляют значительно лучшую способность сопротивляться деформациям сжатия, чем ...

Основы проектирования и конструирования

Скачать

460103

24

39

... ребрами) изображают конструктивные и потоковые функциональные структуры [14]. Принципы построения функциональных структур технических объектов рассматриваются в последующих главах курса "Основы проектирования им конструирования" не включенных в настоящее пособие. Для систем управления существуют характеристики, которые можно использовать в качестве критериев для оценки структур. Одна из них - ...

Сложные деформации. Местные напряжения

Скачать

16454

1

4

... Из выражений (4) и (5) можно найти значение осевого момента сопротивления W поперечного сечения вала как  или  и далее величину диаметра вала . Местные напряжения Напряжения при растяжении (сжатии), изгибе, кручении и сложных деформациях, определяемые по рассмотренным выше зависимостям, называют расчетными или номинальными. Экспериментально установлено, что в местах приложения сил, в местах ...