Навигация
5. Задача Сен-Венана.
Стержень с поперечным сечением в форме равностороннего треугольника высотой а скручивается моментом Mz (рис. 24).
Исследовать напряженное состояние стержня.
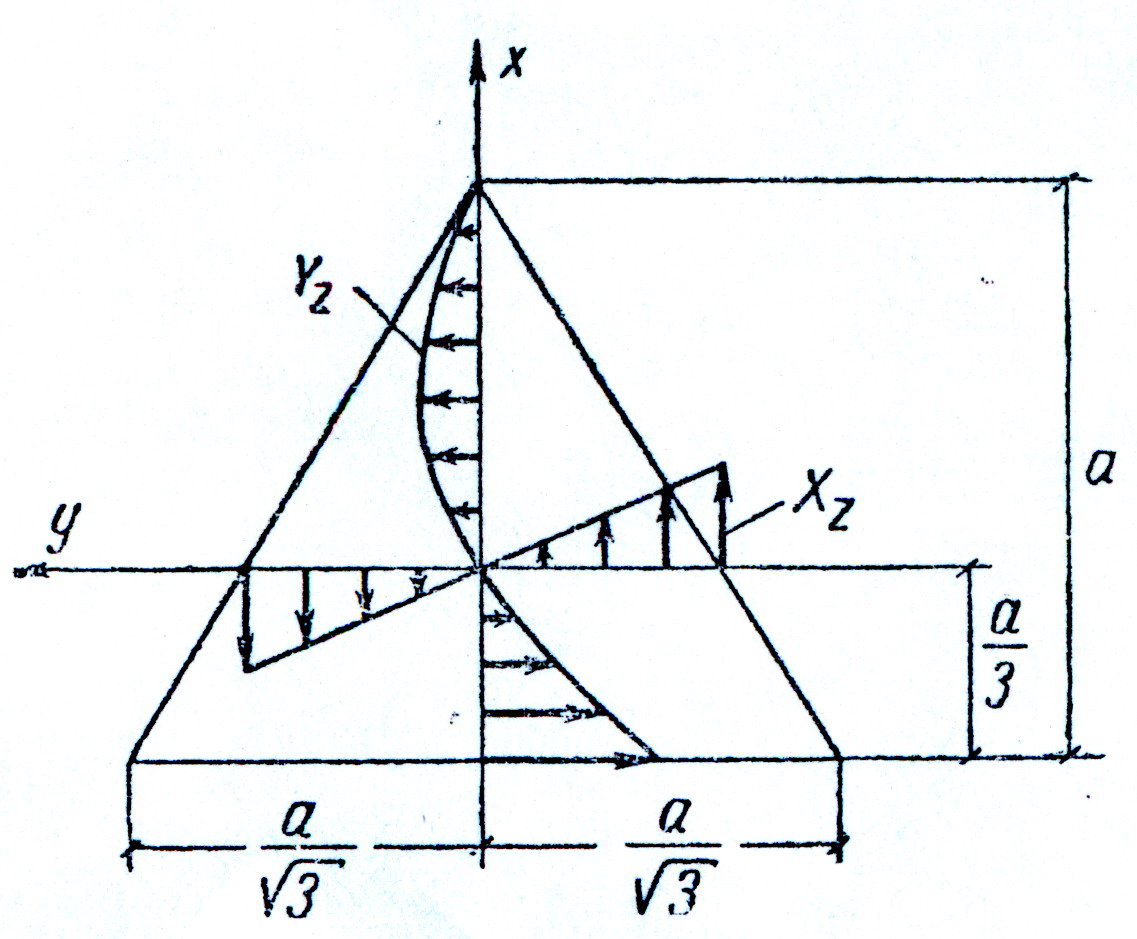
рис.24
Функцию напряжений принимаем в виде:
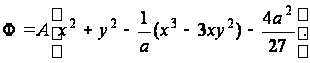(а)
Легко проверить, что на контуре сечения
( x=-a/3
и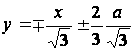 
)
функция Ф обращается в нуль.
Из уравнения (91)
и функция напряжений (а) будет
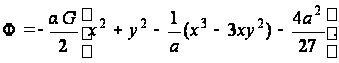(б)
Согласно (90) напряжения
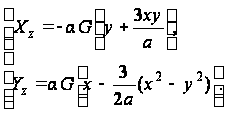(в)
Эпюры напряжений приведены на рис.24.
6. Задача Лейбензона.
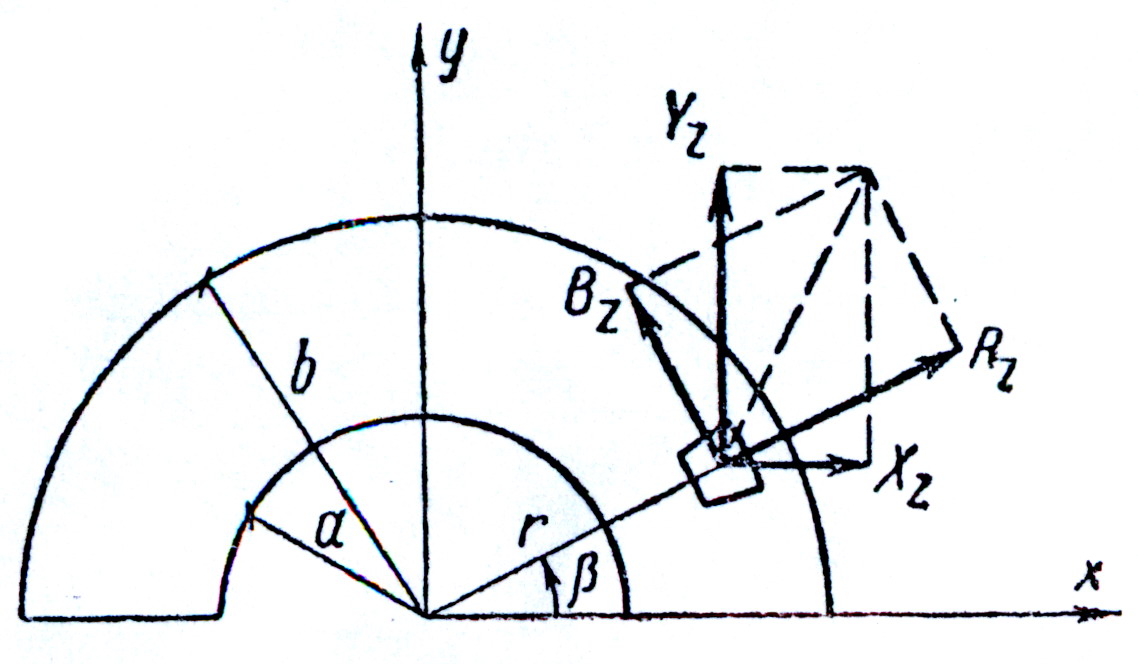
рис.25
Стержень с поперечным сечением в виде полукольца скручивается моментом Mz (рис. 25).
Исследовать напряженное состояние стержня.
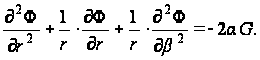(а)
Найдем решение уравнения (а), удовлетворяющее на контуре условию (94) для функции напряжений
Ф=0 (б)
Разложим
правую часть
уравнения (а)
в интервале 
в ряд Фурье:
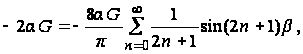(в)
и будем искать решение уравнения (а) в форме ряда
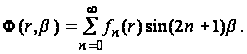(г)
Подставив выражения (в) и (г) в формулу (а), получим определяющее уравнение для fn(r):
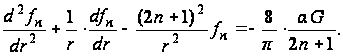(д)
Решая уравнение (д), находим:
(е)
где An и Bn - постоянные интегрирования;
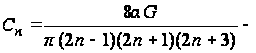
постоянная частного решения. (ж)
Ряд (г) удовлетворяет
условию Ф=0 на
прямолинейных
участках (
и 
).
Из остальных
двух условий:
определяем An и Bn (е). Окончательно получаем:
(з)
Где
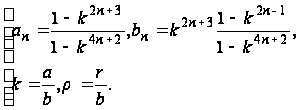(и)
Функция кручения (г) будет
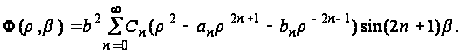(к)
По формулам (90)
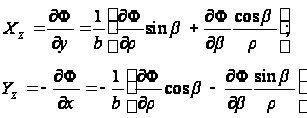
Отсюда, согласно рис. 25,
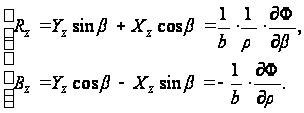(л)
Окончательно получим:
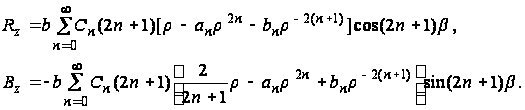
Результирующее
касательное
напряжение
достигает
наибольшего
значения при 
и 
(в середине
дуги полуокружности
большого радиуса).
ЗАКЛЮЧЕНИЕ
Прикладная теория упругости отличается от математической тем, что для решения задач помимо закона Гука применяются некоторые дополнительные гипотезы деформационного характера (гипотеза плоских сечений для стержней, прямых нормалей для тонких пластин и оболочек и т.п.). При решении задач прикладной теории упругости наряду с точными методами решения соответствующих уравнений могут применяться и приближенные методы. Между прикладной теорией упругости, тесно связанной с запросами практики, и сопротивлением материалов нет четкой границы. Некоторые, наиболее простые задачи, относящиеся к этому разделу, рассматриваются также и в курсах сопротивления материалов.
Таким образом, значение теории упругости состоит, во-первых, в получении точных решений для тех задач, которые могут решаться и решаются иными методами в других разделах механики деформируемого тела (сопротивление материалов, строительная механика); во-вторых, в постановке и решении таких важных для практики задач, которые не могут решаться методами сопротивления материалов (задач о напряженном и деформированном состоянии пластин, оболочек, массива, о концентрации напряжений около отверстий, о напряженном состоянии вблизи точек контакта двух тел - контактные задачи, о распространении волн в упругой среде и т.п.); в-третьих, в том, что теория упругости обеспечивает развитие таких дисциплин, как сопротивление материалов и строительная механика, за счет решения круга рассматриваемых в этих дисциплинах задач и использование новых методов решения.
СПИСОК ЛИТЕРАТУРЫ
Галин Л.А. Контактные задачи теории упругости и вязкоупругости. – М.: Наука, 1986. – 304с.
Малинин Н.Н. Прикладная теория пластичности и ползучести. – М.: Машиностроение, 1975. – 320с.
Теребушко О.И. Основы теории упругости и пластичности. – М.: Наука, 1984. – 320с.
Тимошенко С.П., Гудьер Дж. Теория упругости. – М.: Наука, 1975. – 576с.
Регач В.Г. Руководство к решению задач по теории упругости. – М. – 1966.
Ван Цзи-де. Прикладная теория упругости. – М.: ФИЗМАТГИЗ, 1959
Похожие работы
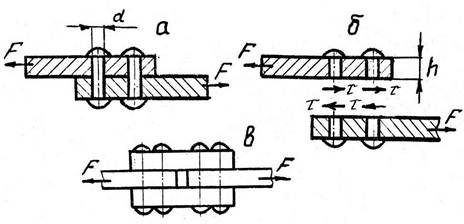
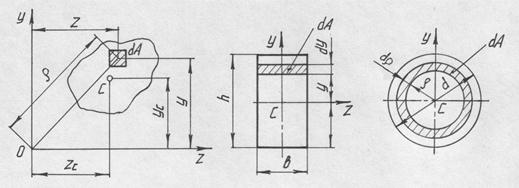
... будут соответственно обозначать диаметр болтов и допускаемое напряжение материала болтов на сдвиг (срез). ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ При рассмотрении деформации растяжения, сжатия, сдвига было установлено, что прочность и жесткость элементов конструкций зависит только от величины поперечного сечения и свойств материала элементов. При деформациях кручения и изгиба, при ...
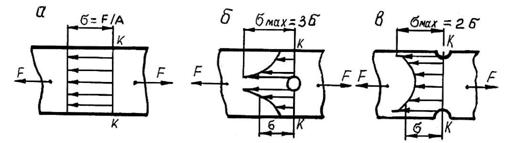
... сечения увеличиваются. Из-за трения между опорными плитами нагружающего устройства и торцевыми поверхностями образца он принимает бочкообразную форму. Для ряда пластичных материалов обнаружить напряжение, аналогичное временному сопротивлению при растяжении, не удается, так как образец сплющивается. Хрупкие материалы проявляют значительно лучшую способность сопротивляться деформациям сжатия, чем ...
... ребрами) изображают конструктивные и потоковые функциональные структуры [14]. Принципы построения функциональных структур технических объектов рассматриваются в последующих главах курса "Основы проектирования им конструирования" не включенных в настоящее пособие. Для систем управления существуют характеристики, которые можно использовать в качестве критериев для оценки структур. Одна из них - ...
... Из выражений (4) и (5) можно найти значение осевого момента сопротивления W поперечного сечения вала как или и далее величину диаметра вала . Местные напряжения Напряжения при растяжении (сжатии), изгибе, кручении и сложных деформациях, определяемые по рассмотренным выше зависимостям, называют расчетными или номинальными. Экспериментально установлено, что в местах приложения сил, в местах ...
0 комментариев