Навигация
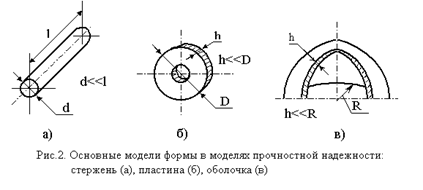
Стержень кругового сечения
2. Стержень кругового сечения
![]()
скручивается моментом Mz.
Исследовать напряженное состояние стержня.
Для функции напряжений принимаем выражение
![]() (a)
(a)
где A- неизвестный множитель.
Согласно уравнению (91)
![]()
Откуда
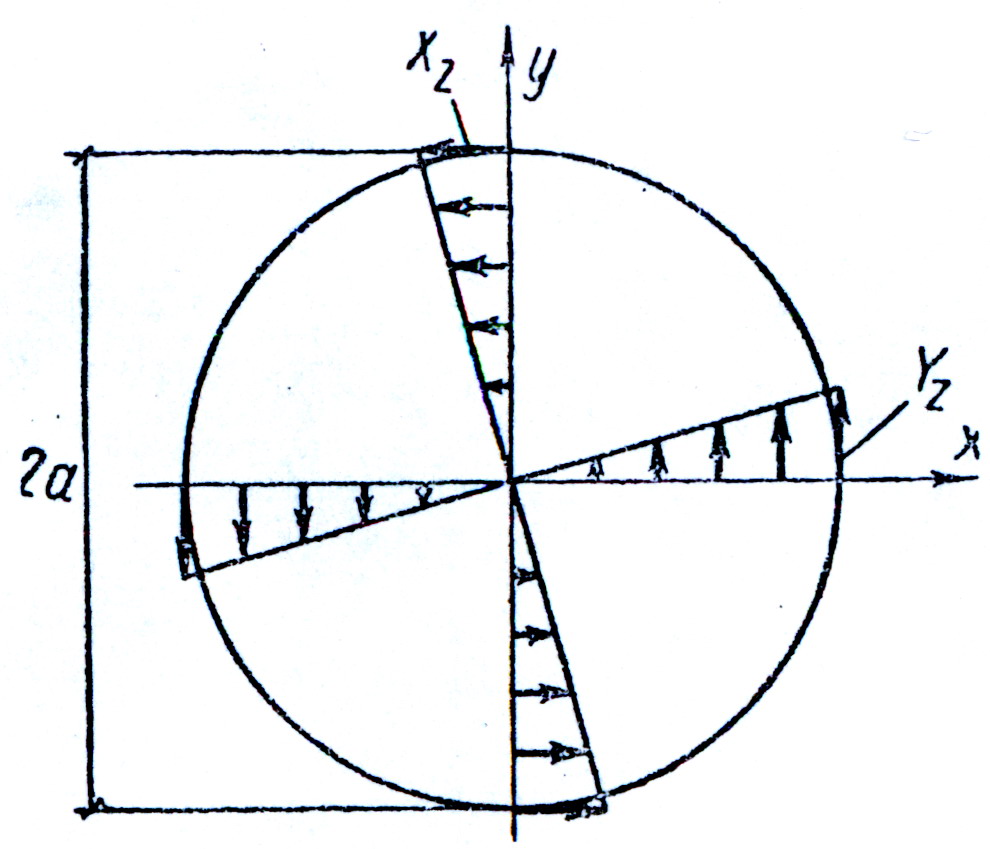
рис.21
![]()
и функция напряжений будет
![]() (б)
(б)
Напряжения определяем согласно формулам (90):
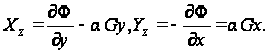 (в)
(в)
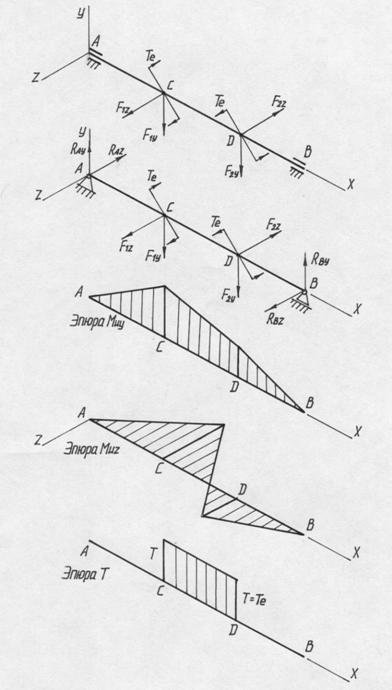
Эпюры напряжений приведены на рис.21.
Согласно формуле (97)
![]()
Наибольшее напряжение
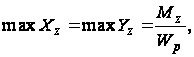 (г)
(г)
где 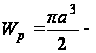 полярный момент
сопротивления.
полярный момент
сопротивления.
Все формулы настоящее задачи являются частным случаем формул задачи (85) при a=b, когда эллипс превращается в круг.
3. Задача Вебера (1921 г.)
Круглый стержень диаметром b с полукруглой выточкой радиуса a скручивается моментом Mz (рис.22).
Найти натяжное состояние стержня.
Уравнения контуров сечения в полярных координатах имеют вид:
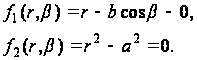 (a)
(a)
Функция напряжений принимает в форме:
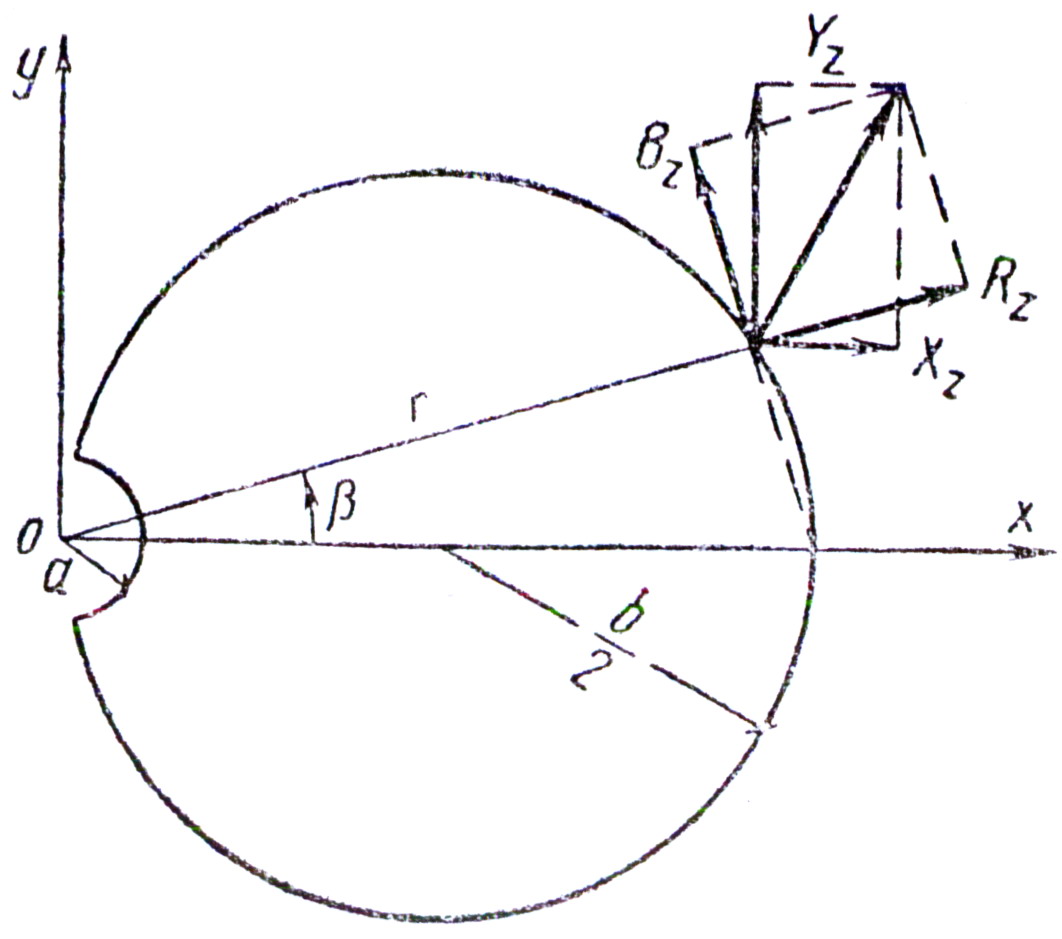
рис.22
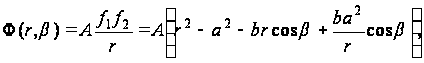 (б)
(б)
где А - неизвестный множитель.
Функция Ф на контуре равна нулю.
В декартовых координатах при
![]()
функция напряжений
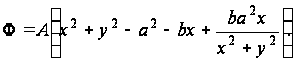
Согласно уравнению (91)
![]()
и функция напряжений будет
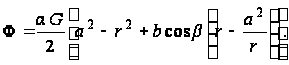 (в)
(в)
Касательные напряжения в полярных координатах, согласно рис.22, равны:
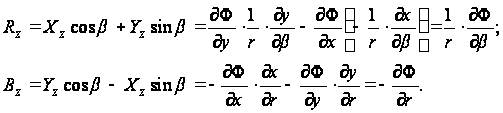
Дифференцируя функцию Ф, получаем:
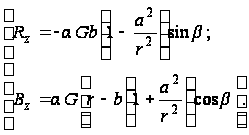 (г)
(г)
Максимальное значение касательное напряжение принимает в точки контура, находящейся на дне выточки:
![]() (д)
(д)
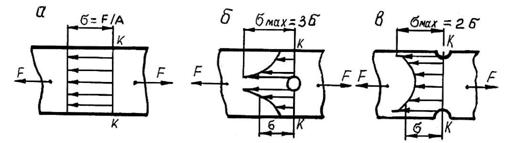
При ![]() оно вдвое больше,
чем на контуре
без выточки
(концентрация
напряжений
у выточек).
оно вдвое больше,
чем на контуре
без выточки
(концентрация
напряжений
у выточек).
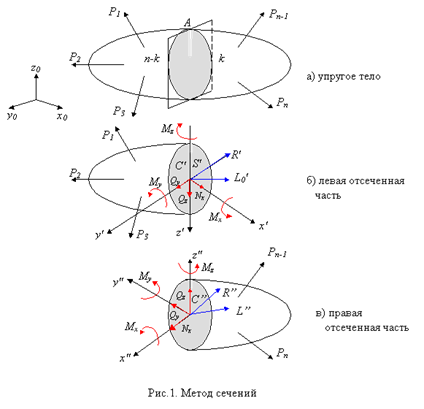
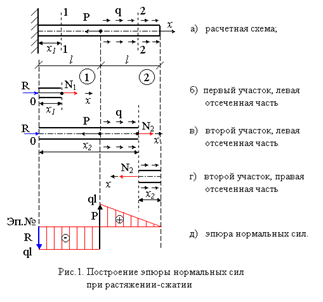
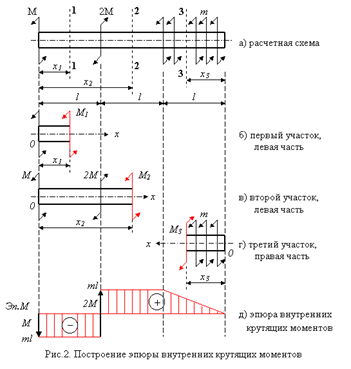
4. Задача Сен-Венана.
Прямоугольный стержень со сторонами a и b (a>b) скручивается моментом Mz (рис.23). Исследовать напряженное состояние стержня.
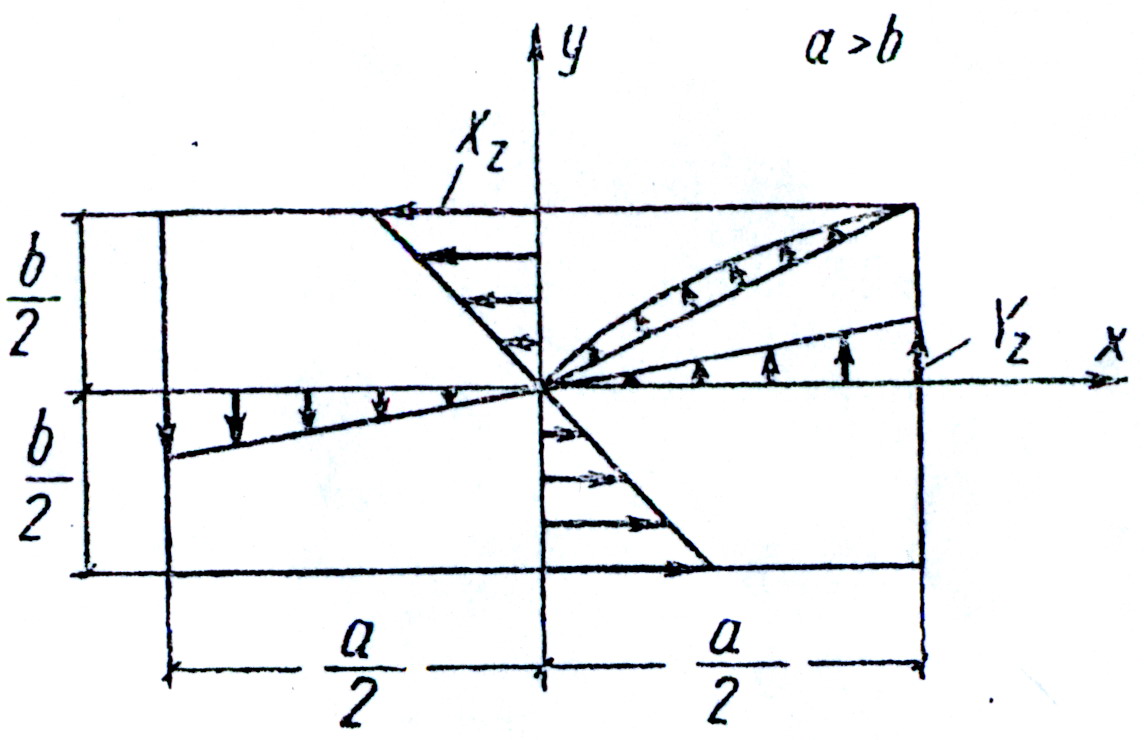
рис.23
Функцию напряжений принимаем в виде:
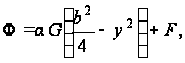 (а)
(а)
где F- неизвестная функция.
Подставив выражение (а) в уравнение (91), найдем, что функция F должна удовлетворять гармоническому уравнению
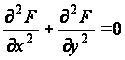 (б)
(б)
и краевым условиям
при ![]()
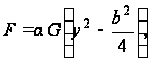
при ![]()
![]()
Согласно методу Фурье будем искать частное решение уравнения (б) в форме:
![]() (в)
(в)
где X(x)-функция от x;
Y(y)-функция от y.
Подставляя функцию F(x,y) в уравнение (б) и разделяя переменные, приходим к уравнениям:
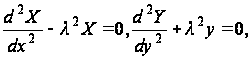 (г)
(г)
где ![]() -
постоянная
величина.
-
постоянная
величина.
Ввиду симметрии задачи решение уравнений (г) берем в виде четных функций
![]()
откуда
(д)
При
![]() F=0,
F=0,
Откуда
![]() и
и 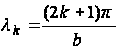 (k=0,
1, 2, …).
(k=0,
1, 2, …).
При
![]()
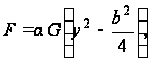
т.е. 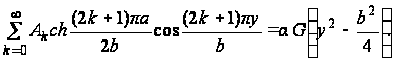 (е)
(е)
Правую часть
равенства (е)
в интервале ![]() раскладываем
в тригонометрический
ряд по косинусам:
раскладываем
в тригонометрический
ряд по косинусам:
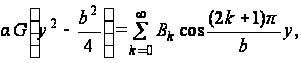 (ж)
(ж)
где 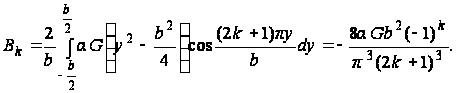
Сравнивая коэффициенты Ak и Bk выражений (е) и (ж), получим:
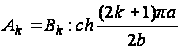
Окончательно функция напряжений будет
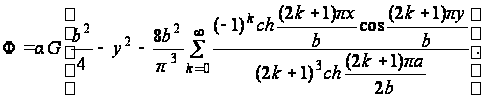 (з)
(з)
Наибольшее
касательное
напряжение
будет в середине
длинных сторон
при x=0
и ![]()
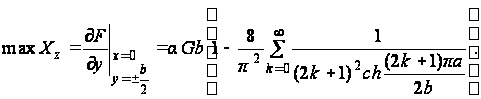 (и)
(и)
Эпюры напряжений приведены на рис.23.
Согласно выражению (97)
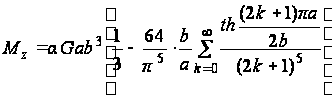 (к)
(к)
Бесконечные ряды при a: b>>1 быстро сходятся.
Для практических расчетов удобно пользоваться формулами:
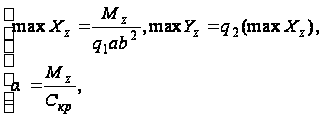 (л)
(л)
где ![]() жесткость
на кручение.
(м)
жесткость
на кручение.
(м)
Значения коэффициентов qi приведены в табл. 3.1.
Таблица 3.1
| a:b | q1 | q2 | q3 | a:b | q1 | q2 | q3 |
1 1,5 2 3 4 | 0,208 0,230 0,246 0,267 0,282 | 1,000 0,860 0,795 0,753 0,745 | 0,140 0,196 0,229 0,263 0,281 | 6 8 10 | 0,298 0,307 0,312 0,333 (1/3) | 0,743 0,743 0,743 0,743 | 0,298 0,307 0,312 0,333 (1/3) |
Похожие работы
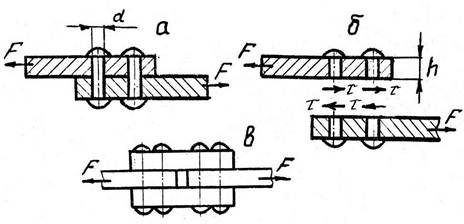
... будут соответственно обозначать диаметр болтов и допускаемое напряжение материала болтов на сдвиг (срез). ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ При рассмотрении деформации растяжения, сжатия, сдвига было установлено, что прочность и жесткость элементов конструкций зависит только от величины поперечного сечения и свойств материала элементов. При деформациях кручения и изгиба, при ...
... сечения увеличиваются. Из-за трения между опорными плитами нагружающего устройства и торцевыми поверхностями образца он принимает бочкообразную форму. Для ряда пластичных материалов обнаружить напряжение, аналогичное временному сопротивлению при растяжении, не удается, так как образец сплющивается. Хрупкие материалы проявляют значительно лучшую способность сопротивляться деформациям сжатия, чем ...
... ребрами) изображают конструктивные и потоковые функциональные структуры [14]. Принципы построения функциональных структур технических объектов рассматриваются в последующих главах курса "Основы проектирования им конструирования" не включенных в настоящее пособие. Для систем управления существуют характеристики, которые можно использовать в качестве критериев для оценки структур. Одна из них - ...
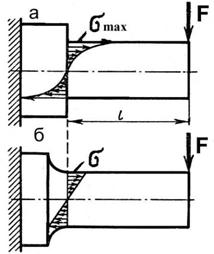
... Из выражений (4) и (5) можно найти значение осевого момента сопротивления W поперечного сечения вала как или и далее величину диаметра вала . Местные напряжения Напряжения при растяжении (сжатии), изгибе, кручении и сложных деформациях, определяемые по рассмотренным выше зависимостям, называют расчетными или номинальными. Экспериментально установлено, что в местах приложения сил, в местах ...





0 комментариев