Навигация
Вычисление определителей
4. Вычисление определителей
Идея последовательного исключения переменных, реализованная в методе Гаусса, может быть использована при вычислении определителей. При этом используются следующие свойства определителей:
1) перестановка двух строк или столбцов определителя не изменяет его абсолютной величины, но меняет знак на противоположный;
2) умножение всех элементов одной строки или одного столбца на любое число равносильно умножению определителя на это число;
3) если к элементам некоторой строки (столбца) определителя прибавить соответствующие элементы другой строки (столбца), умноженные на любой общий множитель, то величина определителя не изменится.
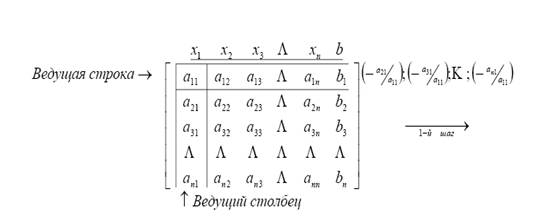
Пусть задан определитель

Выберем главный элемент a11 ¹ 0. Если a11 = 0, то выполним перестановку двух строк или столбцов этого определителя, чтобы получить a11 ¹ 0.
Вынесем главный элемент a11 из первой строки за знак определителя
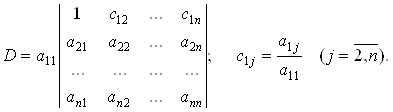
Используя процедуру прямого хода метода Гаусса, преобразуем полученный определитель таким образом, чтобы в первом столбце под единицей были бы все нули. При этом величина определителя не изменится.

Разложим полученный определитель по элементам первого столбца, что даст понижение его порядка определителя на единицу

Повторим указанную процедуру (n - 1) раз и окончательно получим
![]()
Если при вычислении определителя производилась перестановка строк или столбцов (для выбора главного элемента), то
![]()
где s – количество выполненных перестановок.
Таким образом, вычисление определителя detA некоторой матрицы A сводится к выполнению прямого хода метода Гаусса. Абсолютная величина этого определителя равна произведению главных элементов ![]() , k =
, k = ![]() , используемых на каждом шаге прямого хода. Знак определителя зависит от числа перестановок строк и столбцов, выполненных при выборе главных элементов.
, используемых на каждом шаге прямого хода. Знак определителя зависит от числа перестановок строк и столбцов, выполненных при выборе главных элементов.
Если такие перестановки не производились, то величина определителя также может быть вычислена как произведение диагональных элементов матрицы L, формируемой в процессе LU-разложения исходной матрицы А
![]()
5. Вычисление обратных матриц
Обратную матрицу А-1 имеет любая квадратная матрица А, для которой detA ¹ 0. Пусть дана матрица А = [aij]n´n. Для вычисления элементов обратной матрицы используется соотношениеA A-1 = A-1 A= E,
где E – единичная матрица.
Обозначим обратную матрицу A-1 = X = [xij]n´n. Тогда получим
A X= E.
Будем рассматривать столбцы матрицы X как векторы

 …
… 
Аналогично выделим столбцы единичной матрицы E
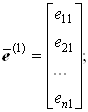
 …;
…; 
Тогда система линейных уравнений вида
A![]() =
= ![]()
позволяет определить элементы k-го столбца обратной матрицы X = A-1. Всего потребуется решить n таких систем с одинаковой матрицей A, но разными правыми частями ![]() для k =
для k = ![]() . Это можно сделать с использованием LU-разложения матрицы коэффициентов A, либо непосредственно с помощью метода Гаусса.
. Это можно сделать с использованием LU-разложения матрицы коэффициентов A, либо непосредственно с помощью метода Гаусса.
6. Итерационные методы
При решении систем уравнений высокого порядка ![]() с разреженными матрицами коэффициентов, которые характерны для большинства задач автоматизации проектирования сложных систем, наиболее эффективно применение итерационных методов. Такие методы (например, последовательных приближений и Зейделя) позволяют получать значения корней системы с заданной точностью в виде последовательности
с разреженными матрицами коэффициентов, которые характерны для большинства задач автоматизации проектирования сложных систем, наиболее эффективно применение итерационных методов. Такие методы (например, последовательных приближений и Зейделя) позволяют получать значения корней системы с заданной точностью в виде последовательности
![]()
некоторых векторов, сходящихся к точному решению X*. Эффективность применения итерационных методов зависит от удачного выбора начального приближения ![]() и скорости сходимости процесса вычислений.
и скорости сходимости процесса вычислений.
Итерационные методы используют особенности разреженных матриц коэффициентов, поскольку ненулевые элементы вычисляются по специальным выражениям по мере необходимости. Поэтому для их реализации требуется меньшее количество вычислительных операций (около n2) и соответствующих затрат машинного времени. Важным преимуществом итерационных методов также является несущественное влияние погрешностей вычислений, так как любое ошибочное приближение может рассматриваться как новый начальный вектор.
Метод последовательных приближений Якоби. Пусть дана система линейных уравнений (1), для которой диагональные элементы
![]() .
.
Тогда переменную x1 можно выразить через первое уравнение, ![]() - через второе уравнение и т. д.
- через второе уравнение и т. д.
 (10)
(10)
где ![]() и
и ![]()
Система (10) называется системой линейных уравнений, приведенной к нормальному виду. Матричная форма записи такой системы представляется как
![]() (11)
(11)
где
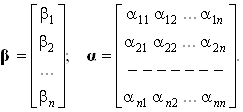
При решении системы (11) за нулевое приближение корней может быть принят столбец свободных членов, т.е. ![]() . Любое k-е приближение (
. Любое k-е приближение (![]() вычисляется по формуле
вычисляется по формуле
![]()
Если последовательность приближений ![]() ,
,![]() ,
,![]() , ...,
, ..., ![]() , ... имеет предел
, ... имеет предел ![]() , то этот предел является точным решением
, то этот предел является точным решением ![]() системы уравнений (2). Итерационная формула, которая может использоваться при программировании метода Якоби, представляется в обозначениях исходной системы (1) следующим образом
системы уравнений (2). Итерационная формула, которая может использоваться при программировании метода Якоби, представляется в обозначениях исходной системы (1) следующим образом
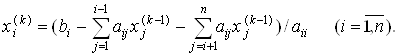
Вычисления продолжаются до тех пор, пока значения ![]() не станут достаточно близкими к
не станут достаточно близкими к ![]() для всех
для всех ![]() Формальное условие прекращения итерационного процесса записывается как
Формальное условие прекращения итерационного процесса записывается как
![]() (12)
(12)
где e - некоторое заданное положительное число, характеризующее точность (погрешность) определения корней системы уравнений.
Итерационный метод Зейделя. Метод Зейделя представляет собой модификацию метода последовательных приближений. При определении значения переменной ![]() на некоторой (k+1)-й итерации используются уже вычисленные (k+1)-е приближения неизвестных
на некоторой (k+1)-й итерации используются уже вычисленные (k+1)-е приближения неизвестных ![]() ,
, ![]() , ...,
, ..., ![]() , а также значения
, а также значения ![]() полученные на предыдущей k-й итерации.
полученные на предыдущей k-й итерации.
Пусть дана линейная система уравнений (10). Выбранные начальные приближения корней ![]() подставляются в первое уравнение
подставляются в первое уравнение
![]()
Для определения ![]() полученное значение
полученное значение ![]() сразу же подставляется во второе уравнение системы
сразу же подставляется во второе уравнение системы
![]()
Аналогично определяются приближения корней ![]() . Значение
. Значение ![]() вычисляется с использованием первых приближений всех переменных
вычисляется с использованием первых приближений всех переменных ![]() как
как
![]()
В общем случае получение значений неизвестных ![]() по методу Зейделя на некоторой k-ой итерации производится по следующей формуле
по методу Зейделя на некоторой k-ой итерации производится по следующей формуле
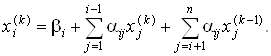
При использовании обозначений исходной системы уравнений (1) итерационная формула обычно записывается как
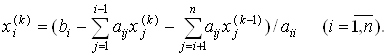
Условие завершения итерационного процесса по методу Зейделя также формулируется в виде соотношения (12). При этом, как правило, процесс сходится к единственному решению быстрее, чем при использовании метода последовательных приближений Якоби.
Условия сходимости итерационных процессов. Пусть дана приведенная к нормальному виду система (11) линейных уравнений. Итерационные процессы последовательных приближений и Зейделя для системы (11) сходятся к единственному решению независимо от выбора начального приближения, если выполняется хотя бы одно из следующих условий
![]()
Приведенные соотношения означают, что сумма модулей элементов любой строки или любого столбца матрицы a должна быть меньше единицы.
Таким образом, для сходимости указанных итерационных процессов достаточно, чтобы значения элементов aij матрицы a при i ¹ j были небольшими по абсолютной величине. Можно показать, что для линейной системы вида (2) итерационные процессы последовательных приближений и Зейделя сходятся к точному решению X*, если для всех уравнений системы модули диагональных коэффициентов удовлетворяют условиям
![]()
и по крайней мере для одного из уравнений выполняется соотношение
![]()
Линейную систему (2) можно заменить такой эквивалентной системой нормального вида (11), которая удовлетворяет условиям сходимости итерационных процессов. Для этого используются следующие элементарные преобразования:
1) перестановка двух строк или столбцов;
2) умножение всех элементов какой-либо строки на одно и то же число, отличное от нуля;
3) сложение элементов какой-либо строки с соответствующими элементами другой строки, умноженными на одно и то же число.
В качестве примера рассмотрим метод [1] приведения линейной системы к виду, удобному для итераций. Система уравнений AX = B умножается на матрицу D = A-1 - D, где D = [dij] - матрица с малыми по модулю элементами. В результате получается эквивалентная система уравнений
(A-1 - D) A X = D B
или в нормальном виде
X = b + a X,
где a = D A и b = D B. Если значения êdij ê достаточно малы, то очевидно, что полученная система вида (9) удовлетворяет условиям сходимости, поскольку умножение на матрицу D эквивалентно совокупности элементарных преобразований над уравнениями системы.
Заключение
Проблема повышения качества вычислений, как несоответствие между желаемым и действительным, существует и будет существовать в дальнейшем. Ее решению будет содействовать развитие информационных технологий, которое заключается как в совершенствовании методов организации информационных процессов, так и их реализации с помощью конкретных инструментов – сред и языков программирования.
Список литературы
1. Бронштейн, И.Н. Справочник по математике для инженеров и учащихся втузов [Текст] И.Н. Бронштейн, К.А. Семендяев. – М.: Наука, 2007. – 708 с.
2. Васильев, Ф.П. Численные методы решения экстремальных задач. [Текст] Ф.П. Васильев – М.: Наука, 2002. C. 415.
3. Симанков, В.С. Основы функционального программирования [Текст] В.С. Симанков, Т.Т. Зангиев, И.В. Зайцев. – Краснодар: КубГТУ, 2002. – 160 с.
4. Калиткин, Н.Н. Численные методы. [Электронный ресурс] Н.Н. Калиткин. – М.: Питер, 2001. С. 504.
5. Кнут, Д.Э. Искусство программирования. Основные алгоритмы [Текст] Д.Э. Кнут. – М.: Вильямс, 2007. Т.1.– 712 с.
Похожие работы
... . При этом собственно нахождение обратной матрицы – процесс достаточно трудоемкий и его программирование вряд ли можно назвать элементарной задачей. Поэтому на практике чаще применяют численные методы решения систем линейных уравнений. К численным методам решения систем линейных уравнений относят такие как: метод Гаусса, метод Крамера, итеративные методы. В методе Гаусса, например, работают над ...
... 35437 x4=0.58554 5 x1=1.3179137 x2=-1.59467 x3=0.35371 x4=0.58462 6 x1=1.3181515 x2=-1.59506 x3=0.35455 x4=0.58557 5. Сравнительный анализ различных методов численного дифференцирования и интегрирования 5.1 Методы численного дифференцирования 5.1.1 Описание метода Предположим, что в окрестности точки xiфункция F (x) дифференцируема достаточное число раз. ...
... на языке Turbo Pascal 7.0 для решении систем линейных алгебраических уравнений, используя метод простой итерации. 1.2 Математическая формулировка задачи Пусть А – невырожденная матрица и нужно решить систему где диагональные элементы матрицы А ненулевые. 1.3 Обзор существующих численных методов решения задачи Метод Гаусса В методе Гаусса матрица СЛАУ с помощью равносильных ...
... числа). Далее по формулам (2) последовательно находятся xn-1 , xn-2 ,…, x1 при i=n-1, n-2,...,1 соответственно. Таким образом, решение уравнений вида (1) описываем способом, называемым методом прогонки, сводится к вычислениям по трём простым формулам: нахождение так называемых прогоночных коэффициентов δi, λiпо формулам (3) при i=1,2,…,n (прямая прогонка) и затем неизвестных xi по ...

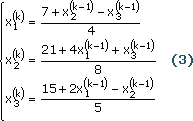
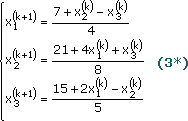
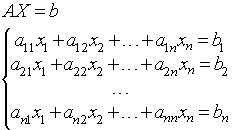
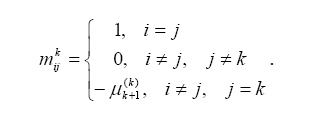
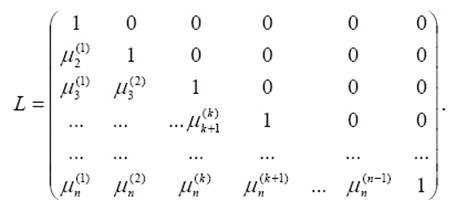
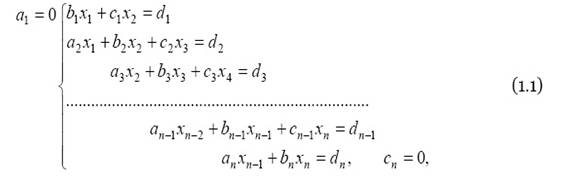
0 комментариев