Навигация
Поверхневі інтеграли другого роду
2. Поверхневі інтеграли другого роду
Введемо поняття сторони поверхні. Візьмемо на гладкій поверхні ![]() довільну точку
довільну точку ![]() , проведемо в ній нормаль
, проведемо в ній нормаль ![]() певного напряму і розглянемо на поверхні
певного напряму і розглянемо на поверхні ![]() довільний замкнений контур, який виходить з точки
довільний замкнений контур, який виходить з точки ![]() і повертається в точку
і повертається в точку ![]() , не перетинаючи при цьому межі поверхні
, не перетинаючи при цьому межі поверхні ![]() . Переміщатимемо точку
. Переміщатимемо точку ![]() по замкненому контуру разом з вектором
по замкненому контуру разом з вектором ![]() так, щоб вектор
так, щоб вектор ![]() весь час залишався нормальним до
весь час залишався нормальним до ![]() . При обході заданого контуру ми можемо повернутися в точку
. При обході заданого контуру ми можемо повернутися в точку ![]() з тим самим або з протилежним напрямом нормалі.
з тим самим або з протилежним напрямом нормалі.
Якщо у довільну точку ![]() поверхні
поверхні ![]() після обходу довільного замкненого контуру, розміщеного на поверхні
після обходу довільного замкненого контуру, розміщеного на поверхні ![]() , який не перетинає її межу, ми повертаємося з початковим напрямом нормалі
, який не перетинає її межу, ми повертаємося з початковим напрямом нормалі ![]() , то поверхню називають двосторонньою.
, то поверхню називають двосторонньою.
Якщо при обході деякого контуру напрям нормалі змінюється на протилежний, то поверхню називають односторонньою.
Прикладами двосторонніх поверхонь є площина, сфера, довільна замкнена поверхня без самоперетинів, довільна поверхня, задана рівнянням ![]() , де
, де ![]() – функції, неперервні в деякій області
– функції, неперервні в деякій області ![]() площини
площини ![]() .
.
Прикладом односторонньої поверхні є так званий лист Мебіуса (рис. 3).

Рисунок 3 – Лист Мебіуса
Модель цієї поверхні можна отримати, якщо прямокутну полоску паперу![]() , перекрутивши один раз, склеїти так, щоб точка
, перекрутивши один раз, склеїти так, щоб точка ![]() збігалася з
збігалася з ![]() , а точка
, а точка ![]() – з
– з ![]() .
.
Двосторонню поверхню називають орієнтовною, а вибір певної її сторони орієнтацією поверхні. Направивши в кожній точці замкненої поверхні нормаль всередину об'єму, обмеженого поверхнею, отримаємо внутрішню сторону поверхні, а направивши нормаль зовні поверхні-зовнішню її сторону. Надалі розглядатимемо двосторонні поверхні. Односторонні поверхні неорієнтовні.
Нехай ![]() – орієнтовна (сторона уже обрана) поверхня, обмежена контуром
– орієнтовна (сторона уже обрана) поверхня, обмежена контуром ![]() , який не має точок самоперетину. Вважатимемо за додатний той напрям обходу контуру
, який не має точок самоперетину. Вважатимемо за додатний той напрям обходу контуру ![]() , при якому спостерігач, розміщений так, що напрям нормалі збігається з напрямом від ніг до голови при русі, залишає поверхню зліва від себе (рис. 4).
, при якому спостерігач, розміщений так, що напрям нормалі збігається з напрямом від ніг до голови при русі, залишає поверхню зліва від себе (рис. 4).
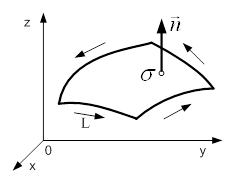
Рисунок 4 – Орієнтовна поверхня ![]()
Протилежний напрям обходу називається від'ємним. Якщо змінити орієнтацію поверхні на протилежну, то додатний і від'ємний напрями обходу контуру ![]() поміняються місцями.
поміняються місцями.
З'ясуємо тепер поняття поверхневого інтеграла другого роду.
Нехай ![]() – гладка поверхня, задана рівнянням
– гладка поверхня, задана рівнянням ![]() і
і ![]() – обмежена функція, визначена в точках поверхні
– обмежена функція, визначена в точках поверхні ![]() . Зорієнтуємо поверхню
. Зорієнтуємо поверхню ![]() . Розіб'ємо її довільно на
. Розіб'ємо її довільно на ![]() частин. Позначимо через
частин. Позначимо через ![]() проекцію
проекцію ![]() -ї частини поверхні
-ї частини поверхні ![]() на площину
на площину ![]() , а через
, а через ![]() – площу
– площу ![]() , взяту із знаком плюс, якщо обрана зовнішня сторона поверхні
, взяту із знаком плюс, якщо обрана зовнішня сторона поверхні ![]() , та із знаком мінус, якщо обрана внутрішня сторона поверхні
, та із знаком мінус, якщо обрана внутрішня сторона поверхні ![]() . Виберемо в кожній частині
. Виберемо в кожній частині ![]() довільну точку
довільну точку ![]() і складемо суму
і складемо суму
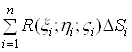 .(6)
.(6)
Вираз (6) називається інтегральною сумою. Нехай ![]() – максимальний діаметр поверхонь
– максимальний діаметр поверхонь ![]() .
.
Якщо при ![]() інтегральні суми (6) мають скінченну границю, яка не залежить ні від способу розбиття поверхні
інтегральні суми (6) мають скінченну границю, яка не залежить ні від способу розбиття поверхні ![]() , ні від вибору точок
, ні від вибору точок ![]() , то цю границю називають поверхневим інтегралом другого роду і позначають так:
, то цю границю називають поверхневим інтегралом другого роду і позначають так: ![]() . Отже, за означенням
. Отже, за означенням
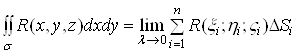 .(7)
.(7)
З означення поверхневого інтеграла другого роду випливає, що при зміні сторони поверхні на протилежну інтеграл змінює знак, бо змінює знак ![]() .
.
Поверхню ![]() можна також проектувати на координатні площини
можна також проектувати на координатні площини ![]() та
та ![]() . Тоді матимемо ще два поверхневі інтеграли
. Тоді матимемо ще два поверхневі інтеграли ![]() , де
, де ![]() – функції, визначені в точках поверхні
– функції, визначені в точках поверхні ![]() .
.
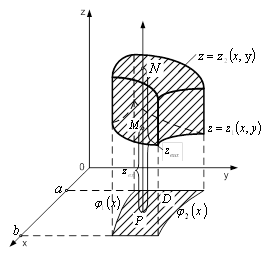
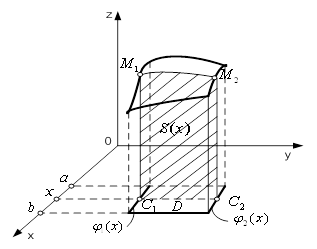
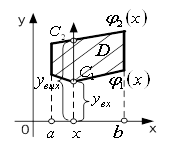
Оскільки ![]() (рис. 5),
(рис. 5),
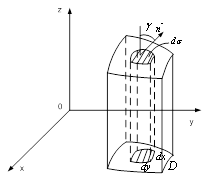
Рисунок 5 – Проекція поверхні ![]() на координатну площину
на координатну площину ![]()
де ![]() – елемент площі поверхні
– елемент площі поверхні ![]() – кути між нормаллю до поверхні
– кути між нормаллю до поверхні ![]() та осями
та осями ![]() відповідно, то справедливі такі формули:
відповідно, то справедливі такі формули:
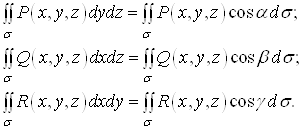
На практиці найпоширенішими є поверхневі інтеграли, які об'єднують усі названі, тобто
![]() .(8)
.(8)
Якщо, наприклад, вектор ![]() є швидкістю рідини, то кількість
є швидкістю рідини, то кількість ![]() рідини, яка протікає через поверхню
рідини, яка протікає через поверхню ![]() за одиницю часу, називається потоком вектора
за одиницю часу, називається потоком вектора ![]() через поверхню
через поверхню ![]() і знаходиться за формулою:
і знаходиться за формулою:
![]() .
.
У цьому полягає фізичний зміст поверхневого інтеграла другого роду. Зрозуміло, коли вектор ![]() має іншу природу, поверхневий інтеграл має інший фізичний зміст.
має іншу природу, поверхневий інтеграл має інший фізичний зміст.
Формула (8) виражає загальний поверхневий інтеграл другого роду через поверхневий інтеграл першого роду.
Поверхневі інтеграли другого роду обчислюються за допомогою подвійних інтегралів.
Нехай функція ![]() неперервна в усіх точках гладкої поверхні
неперервна в усіх точках гладкої поверхні ![]() , яка задана рівнянням
, яка задана рівнянням ![]() , де область
, де область ![]() – проекція поверхні
– проекція поверхні ![]() на площину
на площину ![]() . Виберемо верхню сторону поверхні
. Виберемо верхню сторону поверхні ![]() , де нормаль до поверхні утворює з віссю
, де нормаль до поверхні утворює з віссю ![]() гострий кут, тоді
гострий кут, тоді ![]() . Оскільки
. Оскільки ![]() , то суму (6) можна записати у вигляді
, то суму (6) можна записати у вигляді
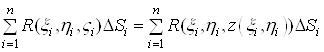 . (9)
. (9)
У правій частині рівності (9) міститься інтегральна сума для функції ![]() . Ця функція неперервна в області
. Ця функція неперервна в області ![]() , тому інтегрована в ній.
, тому інтегрована в ній.
Перейшовши в рівності (9) до границі при ![]() , отримаємо формулу
, отримаємо формулу
![]() ,
,
яка виражає поверхневий інтеграл другого роду по змінних ![]() і
і ![]() через подвійний. Якщо вибрати нижню сторону поверхні (нормаль до поверхні утворює з віссю
через подвійний. Якщо вибрати нижню сторону поверхні (нормаль до поверхні утворює з віссю ![]() тупий кут), то одержаний подвійний інтеграл беруть із знаком «мінус», тому
тупий кут), то одержаний подвійний інтеграл беруть із знаком «мінус», тому
![]() .(10)
.(10)
Аналогічно
![]() ;(11)
;(11)
![]() .(12)
.(12)
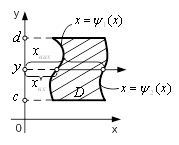
У формулі (11) гладку поверхню ![]() задано рівнянням
задано рівнянням ![]() , а у формулі (12) – рівнянням
, а у формулі (12) – рівнянням ![]() . Знак «плюс» беремо у цих формулах тоді, коли нормаль до поверхні утворює відповідно з віссю
. Знак «плюс» беремо у цих формулах тоді, коли нормаль до поверхні утворює відповідно з віссю ![]() , з віссю
, з віссю ![]() гострий кут, а знак «мінус» – коли тупий кут;
гострий кут, а знак «мінус» – коли тупий кут; ![]() ,
, ![]() – проекції поверхні
– проекції поверхні ![]() на площини
на площини ![]() та
та ![]() відповідно.
відповідно.
Для обчислення загального інтеграла (8) використовують формули (10) – (12), проектуючи поверхню ![]() на всі три координатні площини. Таким чином,
на всі три координатні площини. Таким чином,
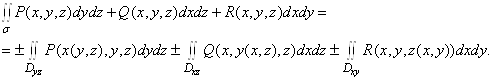
Правильність вибору знаків перед подвійними інтегралами можна перевірити за допомогою формули
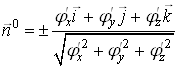 ,
,
яка визначає одиничний нормальний вектор до поверхні ![]() . Подвійний знак у цій формулі відповідає двом сторонам поверхні
. Подвійний знак у цій формулі відповідає двом сторонам поверхні ![]() . З формули (8) випливає, що знак перед подвійним інтегралом збігається із знаком відповідного напрямного косинуса нормалі
. З формули (8) випливає, що знак перед подвійним інтегралом збігається із знаком відповідного напрямного косинуса нормалі ![]() :
:
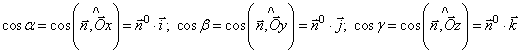 .
.
Якщо поверхня ![]() неоднозначно проектується на будь-яку координатну площину, то цю поверхню розбивають на частини, а інтеграл (8) – на суму інтегралів по одержаних частинах поверхні
неоднозначно проектується на будь-яку координатну площину, то цю поверхню розбивають на частини, а інтеграл (8) – на суму інтегралів по одержаних частинах поверхні ![]() .
.
Похожие работы
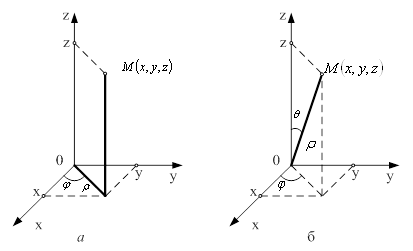
... прямокутних координат до сферичних (рис. 4, б), які пов'язані з формулами Рисунок 4 – Координати: а) циліндричні; б) сферичні ; , якобіан перетворення . З формули (8) знаходимо потрійний інтеграл у сферичних координатах: . (10) Назва «сферичні координати» пов'язана з тим, що координатна поверхня є сферою. При обчисленні потрійного інтеграла в циліндричних чи сферичних ...
... Під знаком границі маємо інтегральну суму, складену для неперервної в області функції . Ця функція інтегровна в області , тому границя у формулі (10) існує і дорівнює подвійному інтегралу (8). 3. Застосування подвійних інтегралів до задач механіки 1. Маса пластини. Нехай на площині маємо матеріальну пластину, яка має форму обмеженої замкненої області , в кожній точці якої густина визначає ...
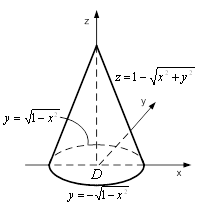
... йного інтеграла зводять до обчислення так званого повторного інтеграла - двох звичайних визначених інтегралів. Покажемо, як це робиться. Припустимо, що при функція . Тоді, згідно з формулою (7), подвійний інтеграл виражає об'єм циліндричного тіла (рис.3) з основою , обмеженого зверху поверхнею . Обчислимо цей об'єм за допомогою методу паралельних перерізів [6]: , де - площа перерізу тіла ...
... прийнятної точності необхідна велика кількість статистичних випробувань. Теорія методу Монте-Карло вивчає способи вибору випадкових величин для вирішення різних завдань, а також способи зменшення дисперсії випадкових величин. 3. Програма обчислення кратного інтеграла методом Монте-Карло Обчислити певний інтеграл . за методом “Монте-Карло” по формулі , де n – число випробувань ;g(x) – щі ...




0 комментариев