Навигация
ПОТРІЙНИЙ ІНТЕГРАЛ
1. Поняття потрійного інтеграла. Умови його існування та властивості
Схема побудови потрійного інтеграла така сама, як і звичайного визначеного інтеграла та подвійного інтеграла.
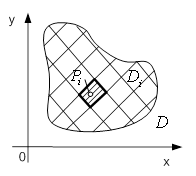
Нехай функція 
визначена в обмеженій замкненій області 
. Розіб'ємо область 
сіткою поверхонь на 
частин 
, які не мають спільних внутрішніх точок і об'єми яких дорівнюють 
. У кожній частині візьмемо довільну точку 
і утворимо суму
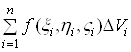,(1)
яка називається інтегральною сумою для функції 
за областю . Нехай 
– найбільший з діаметрів областей .
Якщо інтегральна сума (1) при 
має скінченну границю, яка не залежить ні від способу розбиття області на частини , ні від вибору в них точок 
, то ця границя називається потрійним інтегралом і позначається одним із таких символів:
або 
.
Таким чином, за означенням
,(2)
де – функція, інтегровна в області ; – область інтегрування; 
і 
– змінні інтегрування; 
(або 
) – елемент об'єму.
Якщо по тілу розподілено масу з об'ємною густиною 
в точці 
, то маса 
цього тіла знаходиться за формулою
. (3)
Формула (3) аналогічна формулі (1.8) і може розглядатися як механічний зміст потрійного інтеграла, коли підінтегральна функція невід'ємна в області . Якщо всюди в області покласти 
, то з формули (2) випливає формула для обчислення об'єму 
тіла :
.(4)
Потрійний інтеграл є безпосереднім узагальненням подвійного інтеграла на тривимірний простір. Теорія потрійного інтеграла аналогічна теорії подвійного інтеграла, тому в більшості випадків ми обмежимося лише формулюваннями тверджень і короткими поясненнями.
Теорема (достатня умова інтегровності функції). Якщо функція неперервна в обмеженій замкненій області , то вона в цій області інтегрована.
Властивості потрійних інтегралів.
1. Сталий множник можна винести за знак потрійного інтеграла:
.
Потрійний інтеграл від суми кількох інтегровних функцій дорівнює сумі потрійних інтегралів від доданків:
.
3. Якщо в області інтегрування 
, то
.
4. Якщо функції та 
визначені в одній і тій самій області і 
, то
.
5. (Адитивність потрійного інтеграла.) Якщо область інтегрування функції розбити на частини 
і 
, які не мають спільних внутрішніх точок, то
.
6. (Оцінка потрійного інтеграла.) Якщо функція неперервна в обмеженій замкненій області , яка має об'єм , то
,
де і 
відповідно найменше і найбільше значення функції в області .
7. (Середнє значення функції.) Якщо функція неперервна в обмеженій замкненій області , яка має об'єм , то в цій області існує така точка 
, що
.
Величина
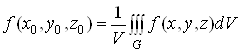
називається середнім значенням функції в області .
Похожие работы
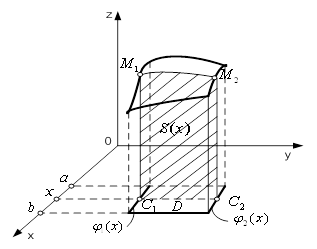
... йного інтеграла зводять до обчислення так званого повторного інтеграла - двох звичайних визначених інтегралів. Покажемо, як це робиться. Припустимо, що при функція . Тоді, згідно з формулою (7), подвійний інтеграл виражає об'єм циліндричного тіла (рис.3) з основою , обмеженого зверху поверхнею . Обчислимо цей об'єм за допомогою методу паралельних перерізів [6]: , де - площа перерізу тіла ...
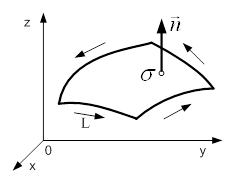
... ія поверхні на координатну площину де – елемент площі поверхні – кути між нормаллю до поверхні та осями відповідно, то справедливі такі формули: На практиці найпоширенішими є поверхневі інтеграли, які об'єднують усі названі, тобто .(8) Якщо, наприклад, вектор є швидкістю рідини, то кількість рідини, яка протікає через поверхню за одиницю часу, називається потоком вектора ...
... Під знаком границі маємо інтегральну суму, складену для неперервної в області функції . Ця функція інтегровна в області , тому границя у формулі (10) існує і дорівнює подвійному інтегралу (8). 3. Застосування подвійних інтегралів до задач механіки 1. Маса пластини. Нехай на площині маємо матеріальну пластину, яка має форму обмеженої замкненої області , в кожній точці якої густина визначає ...
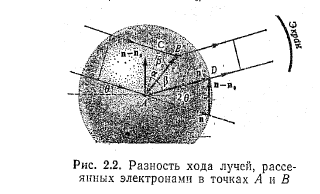
... слабо, лічильник Гейгера реєструє лише невелике число минулих через нього фотонів. Тому ефективність газонаповнених лічильників до цього випромінювання невелика. Ефективнішими для рентгеноструктурних досліджень рідин є сцинтиляційні лічильники. Вони є поєднанням: а) кристала-сцинтилятора йодного натрію, активованого талієм, б) фотоелектронного помножувача (ФЕП); в) попереднього підсилювача на ...
0 комментариев