Навигация
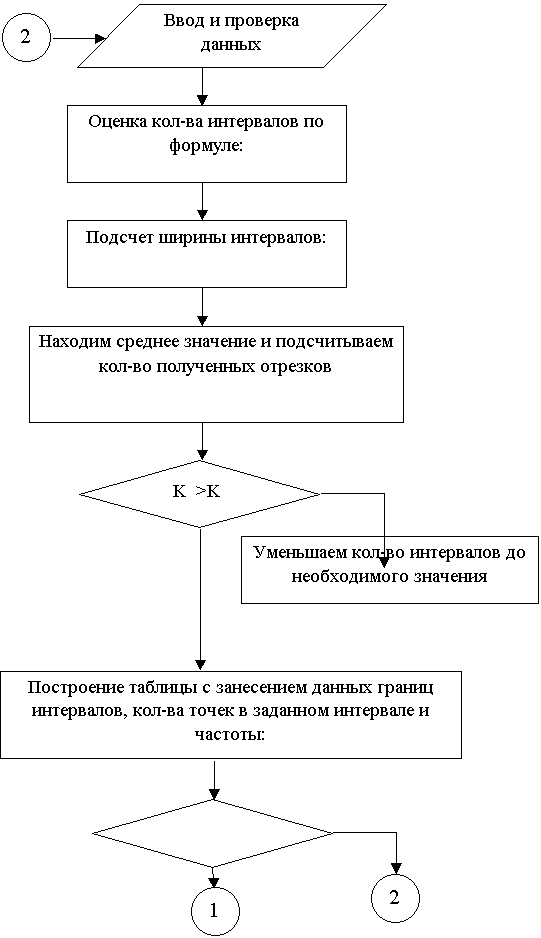
4. Построение гистограммы
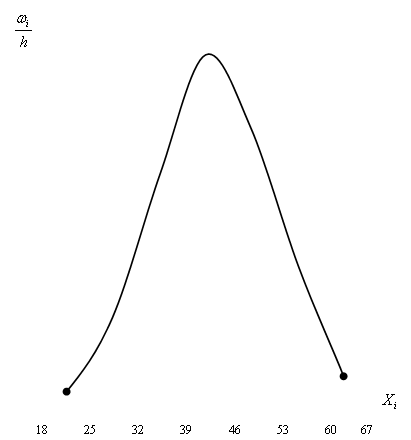
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длины ![]() , а высоты равны отношению
, а высоты равны отношению ![]() – плотность частоты (или
– плотность частоты (или ![]() – плотность частности).
– плотность частности).
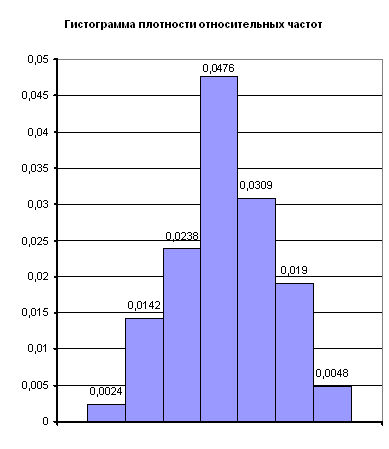
По данным таблицы 4 строим гистограмму (рис. 1).
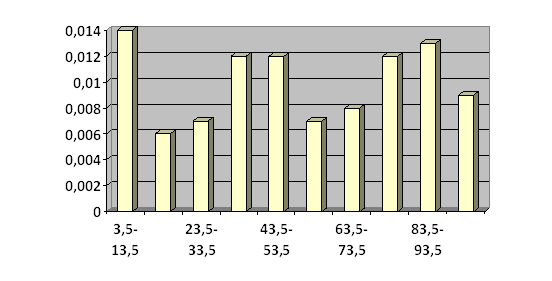 Гистограмма частот является статистическим аналогом дифференциальной функции распределения (плотности)
Гистограмма частот является статистическим аналогом дифференциальной функции распределения (плотности) Выдвижение гипотезы о законе распределения генеральной совокупности
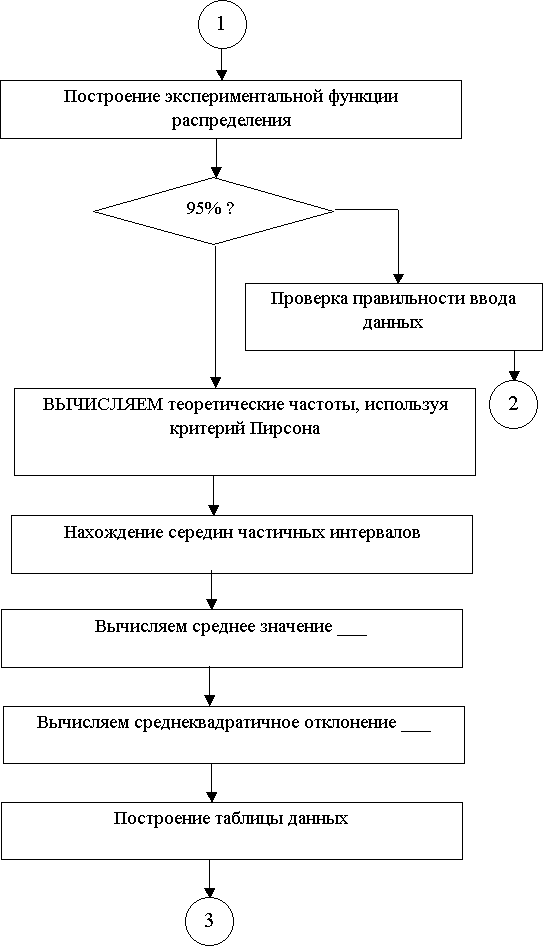
По данным наблюдений статистическое среднее ![]() и выборочное среднее квадратическое отклонение у* по значению почти совпадают. Учитывая данный факт, а также вид гистограммы можно предположить, что случайная величина имеет равномерное распределение.
и выборочное среднее квадратическое отклонение у* по значению почти совпадают. Учитывая данный факт, а также вид гистограммы можно предположить, что случайная величина имеет равномерное распределение.
По виду гистограммы выдвигаем гипотезу о равномерном законе распределения генеральной совокупности Х.
5. Оценка числовых характеристик и параметров закона распределения
Оценками математической статистики называют приближенные значения числовых характеристик или параметров законов распределения генеральной совокупности Х вычисленные на основе выборки.
Оценка называется точечной, если она определяется числом или точкой на числовой оси.
Оценка (как точечная, так и интервальная) является случайной величиной, так как она вычисляется на основе экспериментальных данных и является функцией выборки.
При вычислении точечных оценок для удобства берут не сами элементы выборки, а середины частичных интервалов из интервального вариационного ряда (табл. 1) и применяют формулы:
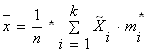
где n - объем выборки, ![]() – i-й элемент выборки
– i-й элемент выборки 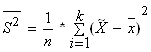
Составим таблицу для нахождения ![]() и
и ![]()


| i |
|
|
| 1 |
| 8.5*14=119 |
| 2 |
| 18.5*6=111 |
| 3 |
| 28.5*7=199.5 |
| 4 |
| 38.5*12=462 |
| 5 |
| 48.5*12=582 |
| 6 |
| 58.5*7=409.5 |
| 7 |
| 68.5*8=548 |
| 8 |
| 78.5*12=942 |
| 9 |
| 88.5*13=1150.5 |
| 10 |
| 98.5*9=886.5 |
|
|
|
Похожие работы
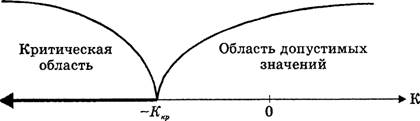
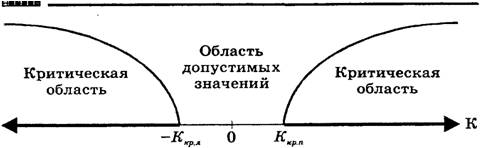
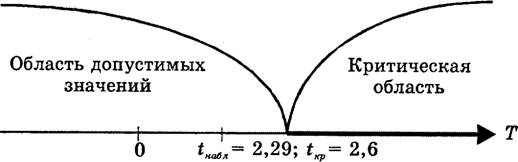
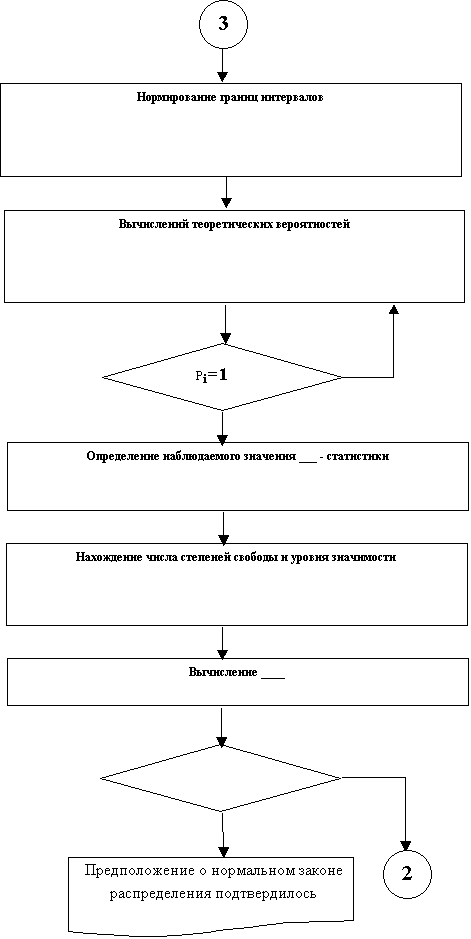
... ошибки первого рода; 3) определить область допустимых значений и так называемую критическую область; 4) принять то или иное решение на основе сравнения фактического и критического значений критерия. Проверка статистических гипотез складывается из следующих этапов: - формулируется в виде статистической гипотезы задача исследования; - выбирается статистическая характеристика гипотезы; - ...
... в таблицу 4 Таблица 4 21.5 0.0025 28.5 0.0114 35.5 0.0291 42.5 0.0425 49.5 0.0351 56.5 0.0165 63.5 0.0044 3. Критерий согласия (Пирсона) Найду соответствующие вероятности для каждого разряда Из ТВ для нормальной случайной величины (8) Значения функции Лапласа, находим в приложении 2, учебника Вентцель Е.С., Овчаров Л.А., теория вероятностей и её ...
... дисперсию, то при условии однородности оценок дисперсий целесообразно принять в качестве ее оценки среднее арифметическое несмещенных оценок дисперсий 1.9. Критерий Пирсона Нормальный закон распределения характеризуется плотностью вероятности вида где M{X}, ____ — соответственно математическое ожидание и дисперсия случайной величины. согласованности изучаемого распределения с ...
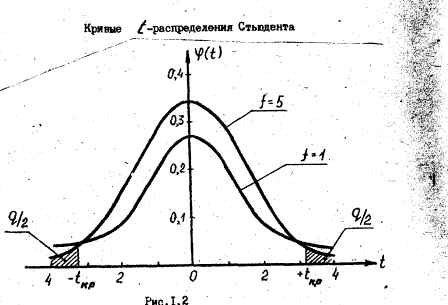
... теоретическим и эмпирическим распределением. Примечание: Построенные графики находятся в приложениях к работе. 6* Проверить гипотезу о нормальном законе распределения по критерию согласи яПирсона f^2). Проверка гипотез о нормальном законе распределения Частоты для проверки соответствия эмпирического ряда распределения нормальному закону используют критерий X^2, основанный на сравнении ...
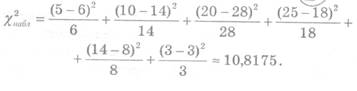
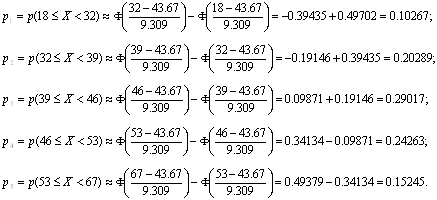

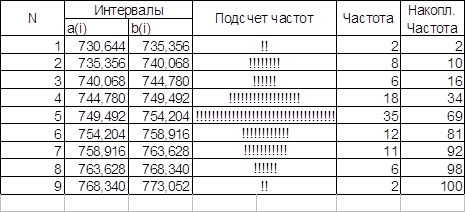
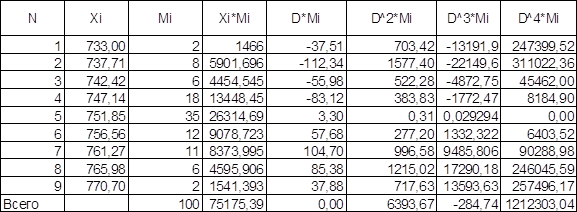
0 комментариев