Навигация
Заміна змінних в потрійному інтегралі
3. Заміна змінних в потрійному інтегралі
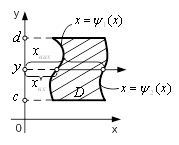
Заміну змінної в потрійному інтегралі виконують за таким правилом: якщо обмежена замкнена область ![]() взаємно однозначно відображується на область
взаємно однозначно відображується на область ![]() за допомогою неперервно диференційовних функцій
за допомогою неперервно диференційовних функцій ![]() ,
, ![]() ,
, ![]() , якобіан
, якобіан ![]() в області
в області ![]() не дорівнює нулю:
не дорівнює нулю:

і ![]() – неперервна в
– неперервна в ![]() , то справедлива формула
, то справедлива формула
![]() . (8)
. (8)
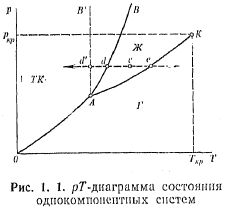
На практиці найуживанішими є циліндричні та сферичні координати. При переході від прямокутних координат ![]() до циліндричних
до циліндричних ![]() (рис.4, а), пов'язаних з
(рис.4, а), пов'язаних з ![]() співвідношеннями
співвідношеннями
![]() ;
;
![]() ,
,
якобіан перетворення
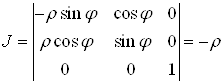 .
.
З формули (8) отримуємо потрійний інтеграл у циліндричних координатах:
![]() .(9)
.(9)
Назва «циліндричні координати» пов'язана з тим, що координатна поверхня ![]() є циліндром, прямолінійні твірні якого паралельні осі
є циліндром, прямолінійні твірні якого паралельні осі ![]() .
.
При переході від прямокутних координат ![]() до сферичних
до сферичних ![]()
(рис. 4, б), які пов'язані з ![]() формулами
формулами
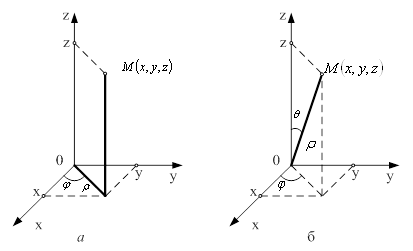
Рисунок 4 – Координати: а) циліндричні; б) сферичні
![]() ;
;
![]() ,
,
якобіан перетворення
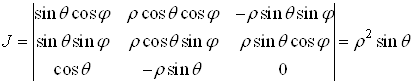 .
.
З формули (8) знаходимо потрійний інтеграл у сферичних координатах:
![]() . (10)
. (10)
Назва «сферичні координати» пов'язана з тим, що координатна поверхня ![]() є сферою. При обчисленні потрійного інтеграла в циліндричних чи сферичних координатах область
є сферою. При обчисленні потрійного інтеграла в циліндричних чи сферичних координатах область ![]() , як правило, не будують, а межі інтегрування знаходять безпосередньо за областю
, як правило, не будують, а межі інтегрування знаходять безпосередньо за областю ![]() , користуючись геометричним змістом нових координат. При цьому рівняння поверхонь
, користуючись геометричним змістом нових координат. При цьому рівняння поверхонь ![]() та
та ![]() , які обмежують область
, які обмежують область ![]() , записують у нових координатах.
, записують у нових координатах.
Зокрема, якщо область ![]() обмежена циліндричною поверхнею
обмежена циліндричною поверхнею ![]() та площинами
та площинами ![]() , то всі межі інтегрування в циліндричній системі координат сталі:
, то всі межі інтегрування в циліндричній системі координат сталі:
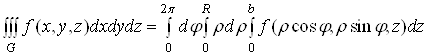
і не змінюються при зміні порядку інтегрування. Те саме буде у сферичних координатах у випадку, коли ![]() – куля:
– куля: ![]() або кульове кільце. Наприклад, якщо
або кульове кільце. Наприклад, якщо ![]() – кульове кільце з внутрішньою сферою
– кульове кільце з внутрішньою сферою ![]() , то рівняння цієї сфери в сферичних координатах має вигляд
, то рівняння цієї сфери в сферичних координатах має вигляд
![]()
або
![]() ,
,
звідки ![]() . Аналогічно
. Аналогічно ![]() – рівняння зовнішньої сфери, тому
– рівняння зовнішньої сфери, тому
![]() .
.
У випадку, коли ![]() – куля
– куля ![]() , у цій формулі слід покласти
, у цій формулі слід покласти ![]() . Інших будь-яких загальних рекомендацій, коли необхідно переходити до тієї чи іншої системи координат, дати неможливо. Це залежить і від області інтегрування, і від підінтегральної функції. Іноді потрібно написати інтеграл у різних системах координат і лише після цього вирішити, в якій з них обчислення буде найпростішим.
. Інших будь-яких загальних рекомендацій, коли необхідно переходити до тієї чи іншої системи координат, дати неможливо. Це залежить і від області інтегрування, і від підінтегральної функції. Іноді потрібно написати інтеграл у різних системах координат і лише після цього вирішити, в якій з них обчислення буде найпростішим.
Приклад
1. Обчислити інтеграл ![]() , якщо область
, якщо область ![]() обмежена поверхнями
обмежена поверхнями ![]() і
і ![]() .
.
Розв’язання
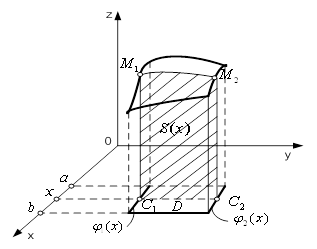
Область ![]() є конусом (рис. 5).
є конусом (рис. 5).
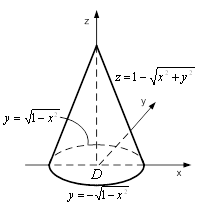
Рисунок 5 – Область ![]()
Рівняння конічної поверхні, яка обмежує область ![]() , можна записати у вигляді
, можна записати у вигляді ![]() , а саму область
, а саму область ![]() подати таким чином:
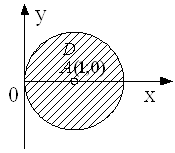
подати таким чином: ![]() , де
, де ![]() – круг радіуса
– круг радіуса ![]() з центром
з центром ![]() . Тому даний потрійний інтеграл можна звести до послідовного обчислення трьох визначених інтегралів у прямокутних координатах:
. Тому даний потрійний інтеграл можна звести до послідовного обчислення трьох визначених інтегралів у прямокутних координатах:
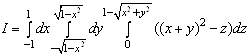 .
.
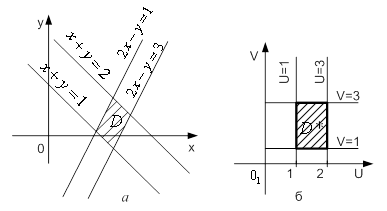
Проте зручніше перейти до циліндричних координат ![]() . Тоді прообраз круга
. Тоді прообраз круга ![]() є прямокутник
є прямокутник ![]() , прообраз конічної поверхні – плоска поверхня
, прообраз конічної поверхні – плоска поверхня ![]() , а прообраз області
, а прообраз області ![]() – область
– область ![]() . Якобіан переходу до циліндричних координат дорівнює
. Якобіан переходу до циліндричних координат дорівнює ![]() , підінтегральна функція в циліндричних координатах дорівнює
, підінтегральна функція в циліндричних координатах дорівнює![]() . Зводячи потрійний інтеграл за областю
. Зводячи потрійний інтеграл за областю ![]() до послідовного обчислення трьох визначних інтегралів, отримаємо
до послідовного обчислення трьох визначних інтегралів, отримаємо
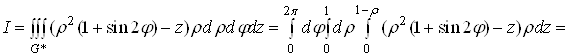
![]()
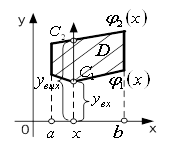
Зазначимо, що розставлення меж інтегрування в циліндричних координатах, як правило, виконують, розглядаючи не область ![]() , а зміну циліндричних координат в області
, а зміну циліндричних координат в області ![]() . Наочно видно, що в області
. Наочно видно, що в області ![]() змінна
змінна ![]() змінюється від
змінюється від ![]() до
до ![]() , при кожному значенні
, при кожному значенні ![]() змінна
змінна ![]() змінюється від
змінюється від ![]() до
до ![]() , а для кожної точки
, а для кожної точки ![]() області
області ![]() змінна
змінна ![]() змінюється в області
змінюється в області ![]() від
від ![]() (значення
(значення ![]() в області
в області ![]() ) до
) до ![]() (значення
(значення ![]() на конічній поверхні).
на конічній поверхні).
4. Деякі застосування потрійного інтеграла
інтеграл потрійний обчислення змінний
1. Обчислення об'ємів. Якщо деяке тіло є обмеженою і замкненою
областю ![]() , що має об'єм
, що має об'єм ![]() , то згідно з формулою (4)
, то згідно з формулою (4)
![]() .(11)
.(11)
Застосування у механіці. Нехай ![]() – обмежена замкнена область простору
– обмежена замкнена область простору ![]() , яку займає деяке матеріальне тіло з густиною
, яку займає деяке матеріальне тіло з густиною ![]() , де
, де ![]() – неперервна функція в області
– неперервна функція в області ![]() , тоді:
, тоді:
а)маса цього тіла
![]() ;(12)
;(12)
б)моменти інерції ![]() тіла відносно координатних осей
тіла відносно координатних осей ![]() відповідно дорівнюють
відповідно дорівнюють
![]() . (13)
. (13)
Моменти інерції ![]() тіла відносно координатних площин
тіла відносно координатних площин ![]() обчислюються за формулами
обчислюються за формулами
![]() .(14)
.(14)
Момент інерції тіла відносно початку координат
![]()
![]() (15)
(15)
в) статичні моменти ![]() тіла відносно координатних площин
тіла відносно координатних площин ![]() обчислюються за формулами
обчислюються за формулами
![]() ;(16)
;(16)
г) координати ![]() центра маси тіла визначаються за формулами
центра маси тіла визначаються за формулами
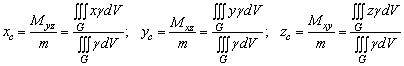 . (17)
. (17)
Доведення формули (11), як уже зазначалося, випливає з означення потрійного інтеграла:
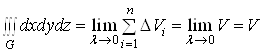 .
.
Похожие работы
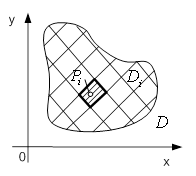
... йного інтеграла зводять до обчислення так званого повторного інтеграла - двох звичайних визначених інтегралів. Покажемо, як це робиться. Припустимо, що при функція . Тоді, згідно з формулою (7), подвійний інтеграл виражає об'єм циліндричного тіла (рис.3) з основою , обмеженого зверху поверхнею . Обчислимо цей об'єм за допомогою методу паралельних перерізів [6]: , де - площа перерізу тіла ...
... ія поверхні на координатну площину де – елемент площі поверхні – кути між нормаллю до поверхні та осями відповідно, то справедливі такі формули: На практиці найпоширенішими є поверхневі інтеграли, які об'єднують усі названі, тобто .(8) Якщо, наприклад, вектор є швидкістю рідини, то кількість рідини, яка протікає через поверхню за одиницю часу, називається потоком вектора ...
... Під знаком границі маємо інтегральну суму, складену для неперервної в області функції . Ця функція інтегровна в області , тому границя у формулі (10) існує і дорівнює подвійному інтегралу (8). 3. Застосування подвійних інтегралів до задач механіки 1. Маса пластини. Нехай на площині маємо матеріальну пластину, яка має форму обмеженої замкненої області , в кожній точці якої густина визначає ...
... слабо, лічильник Гейгера реєструє лише невелике число минулих через нього фотонів. Тому ефективність газонаповнених лічильників до цього випромінювання невелика. Ефективнішими для рентгеноструктурних досліджень рідин є сцинтиляційні лічильники. Вони є поєднанням: а) кристала-сцинтилятора йодного натрію, активованого талієм, б) фотоелектронного помножувача (ФЕП); в) попереднього підсилювача на ...

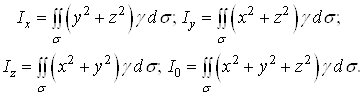



0 комментариев