Навигация
Лінійні перетворення (оператори) із простору V в V
2. Лінійні перетворення (оператори) із простору V в V
В подальшому будемо розглядати лінійні оператори, діючі із лінійного простору ![]() в той самий простір. Ці оператори називають також перетвореннями із
в той самий простір. Ці оператори називають також перетвореннями із ![]() в
в ![]() .
.
Назвемо тотожнім (одиничним) оператор ![]() такий, що для любого вектора
такий, що для любого вектора ![]() простору
простору ![]() . Очевидно,
. Очевидно, ![]() ,
, ![]() , для любих
, для любих ![]() . З цього випливає, оператор
. З цього випливає, оператор ![]() – лінійний і, тому,
– лінійний і, тому, ![]() . Неважко упевнитися в тому, що оператор
. Неважко упевнитися в тому, що оператор ![]() – єдиний. Дійсно, якщо припустити що, крім тотожного оператора
– єдиний. Дійсно, якщо припустити що, крім тотожного оператора ![]() з
з ![]() , існує ще один тотожний оператор
, існує ще один тотожний оператор ![]() , тоді для будь-якого
, тоді для будь-якого ![]() будемо мати
будемо мати ![]() ,
, ![]() , очевидно,
, очевидно, ![]() , тобто
, тобто ![]() .
.
Введемо операцію множення операторів. Нехай ![]() та
та ![]() – два будь-яких лінійних оператора з
– два будь-яких лінійних оператора з ![]() , а
, а ![]() – довільний вектор простору
– довільний вектор простору ![]() . Очевидно вектор
. Очевидно вектор ![]() , тому цей вектор можна привести за допомогою оператора
, тому цей вектор можна привести за допомогою оператора ![]() . В результаті вектор
. В результаті вектор ![]() буде перетворений до вектору
буде перетворений до вектору ![]() . Оператор, який приводить довільний вектор
. Оператор, який приводить довільний вектор ![]() простору
простору ![]() у вектор
у вектор ![]() , називається добутком операторів
, називається добутком операторів ![]() та
та ![]() і позначається так:
і позначається так: ![]() . За означенням добутку операторів
. За означенням добутку операторів ![]() і
і ![]()
![]() для будь-якого вектору
для будь-якого вектору ![]() . Легко перевірити, що
. Легко перевірити, що ![]()
![]() ,
, ![]() , де
, де ![]() – довільно вибране комплексне число. З цього слідує, що добуток лінійних операторів є лінійним оператором, тобто
– довільно вибране комплексне число. З цього слідує, що добуток лінійних операторів є лінійним оператором, тобто ![]() . Зауважимо, що
. Зауважимо, що ![]() .
.
Операції додавання та множення лінійних операторів мають наступні властивості
1) ![]() , 3)
, 3) ![]() ,
,
2) ![]() , 4)
, 4) ![]() .
.
Для ілюстрації способу доведення цих властивостей доведемо властивість ![]() . Нехай
. Нехай ![]() – довільний вектор простору
– довільний вектор простору ![]() . Для довільного вектору
. Для довільного вектору ![]() простору
простору ![]() за означенням добутку і суми операторів має
за означенням добутку і суми операторів має

Таким чином, ![]() , тобто
, тобто ![]() .
.
Якщо для оператору ![]() можна вказати такий лінійний оператор
можна вказати такий лінійний оператор ![]() , що
, що ![]() , то оператор
, то оператор ![]() називають оберненим для оператору
називають оберненим для оператору ![]() . Можна показати, що оператор
. Можна показати, що оператор ![]() – єдиний.
– єдиний.
Покажемо, що оператор ![]() , що має обернений, перетворює ненульовий вектор в ненульовий, тобто якщо
, що має обернений, перетворює ненульовий вектор в ненульовий, тобто якщо ![]() , то й
, то й ![]() . Спочатку доведемо, що
. Спочатку доведемо, що ![]() . Дійсно, так як
. Дійсно, так як ![]() – лінійний оператор, то для будь-якого
– лінійний оператор, то для будь-якого ![]()
![]() . Доведене твердження справедливе для будь-якого лінійного оператора, в тому числі і для оператора, що має обернений, і для оператора
. Доведене твердження справедливе для будь-якого лінійного оператора, в тому числі і для оператора, що має обернений, і для оператора ![]() . Нехай
. Нехай ![]() і
і ![]() . Так як оператор
. Так як оператор ![]() має обернений, то
має обернений, то ![]() , тобто
, тобто ![]() . Якщо припустити, що деякому
. Якщо припустити, що деякому ![]() відповідає вектор
відповідає вектор ![]() , тоді на основі установлених рівностей
, тоді на основі установлених рівностей ![]() і
і ![]() виходило б, що
виходило б, що ![]() . А це заперечує початковому фактові, що
. А це заперечує початковому фактові, що ![]() . З цього випливає, що припущення про те, що для деякого
. З цього випливає, що припущення про те, що для деякого ![]()
![]() , невірно, тому для будь – якого
, невірно, тому для будь – якого ![]()
![]() .
.
Доведемо ще одну властивість оператора ![]() , що має обернений. Такий оператор два різних вектора
, що має обернений. Такий оператор два різних вектора ![]() та
та ![]() перетворює у два різні вектори
перетворює у два різні вектори ![]() і
і ![]() . Дійсно, якщо припустити противне, що існують такі нерівні один одному
. Дійсно, якщо припустити противне, що існують такі нерівні один одному ![]() і
і ![]() , для яких
, для яких ![]() , тоді для таких
, тоді для таких ![]() і
і ![]()
![]() або, що те саме
або, що те саме ![]() . За умовою оператор
. За умовою оператор ![]() має обернений. За доведеною вище властивістю такого оператора із рівності
має обернений. За доведеною вище властивістю такого оператора із рівності ![]() випливає, що
випливає, що ![]() , тобто
, тобто ![]() . Ми прийшли до протиріччя з тим фактом, що за умовою
. Ми прийшли до протиріччя з тим фактом, що за умовою ![]() . З цього випливає, що будь – яким двом різним векторам
. З цього випливає, що будь – яким двом різним векторам ![]() і
і ![]() відповідають різні образи
відповідають різні образи ![]() і
і ![]() .
.
Оператор ![]() називають взаємно – однозначним, якщо два будь – які різні вектори
називають взаємно – однозначним, якщо два будь – які різні вектори ![]() і
і ![]() він перетворює у різні вектори
він перетворює у різні вектори ![]() і
і ![]() . Із наведеного вище випливає, що оператор
. Із наведеного вище випливає, що оператор ![]() , що має обернений, є взаємно – однозначним. Для взаємно – однозначного оператора неважко довести таку властивість: якщо
, що має обернений, є взаємно – однозначним. Для взаємно – однозначного оператора неважко довести таку властивість: якщо ![]() , то і
, то і ![]() . Покажемо, що взаємно – однозначний оператор
. Покажемо, що взаємно – однозначний оператор ![]() лінійно незалежні вектори
лінійно незалежні вектори ![]() ,
, ![]() , …,
, …, ![]() перетворює в лінійно незалежні вектори
перетворює в лінійно незалежні вектори ![]() ,
, ![]() , …,
, …, ![]() . Для доведення цього твердження скористаємося методом «від противного». Припустимо противне, що вектори
. Для доведення цього твердження скористаємося методом «від противного». Припустимо противне, що вектори ![]() , …,
, …, ![]() – лінійно незалежні. Тоді можна знайти такі не рівню нулю числа,
– лінійно незалежні. Тоді можна знайти такі не рівню нулю числа, ![]() що
що ![]() . Так як оператор
. Так як оператор ![]() – лінійний, то
– лінійний, то ![]() .
.
Звідси за властивістю взаємно-однозначного оператора ![]() , тобто вектори
, тобто вектори ![]() ,
, ![]() , …,
, …, ![]() виявляються лінійно залежними. Протиріччя з умовою ствердження означає, що вектори
виявляються лінійно залежними. Протиріччя з умовою ствердження означає, що вектори ![]() ,
, ![]() , …,
, …, ![]() лінійно незалежні.
лінійно незалежні.
Із доведеного випливає, що будь-який вектор ![]() простору
простору ![]() має єдиний прообраз
має єдиний прообраз ![]() такий, що
такий, що ![]() . Доведемо тільки єдність прообразу вектора
. Доведемо тільки єдність прообразу вектора ![]() . Дійсно, якщо припустити, що вектор
. Дійсно, якщо припустити, що вектор ![]() має декілька різноманітних прообразів, наприклад,
має декілька різноманітних прообразів, наприклад, ![]() і
і ![]() , то виявиться, що
, то виявиться, що ![]() . Звідси
. Звідси ![]() , маємо
, маємо ![]() , так як оператор взаємно-однозначний. Отже, якщо оператор
, так як оператор взаємно-однозначний. Отже, якщо оператор ![]() – взаємно-однозначний, то кожному вектору
– взаємно-однозначний, то кожному вектору ![]() простору
простору ![]() він ставить у відповідність один і тільки один вектор
він ставить у відповідність один і тільки один вектор ![]() . Звідси випливає, що взаємно-однозначний оператор має обернений.
. Звідси випливає, що взаємно-однозначний оператор має обернений.
Підводячи підсумок сказаному вище про властивості оберненого і взаємно-однозначного операторів, сформулюємо наступне твердження.
Теорема 2.1. Для того, щоб лінійний оператор ![]() мав обернений необхідно і достатньо, щоб він був взаємно-однозначним.
мав обернений необхідно і достатньо, щоб він був взаємно-однозначним.
Введемо поняття ядра й образу оператора. Ядром лінійного оператора ![]() називають таку множину
називають таку множину ![]() векторів простору
векторів простору ![]() , що для любого
, що для любого ![]()
![]() . Відомо, що будь-який лінійний оператор приводить вектор
. Відомо, що будь-який лінійний оператор приводить вектор ![]() в
в ![]() , тобто
, тобто ![]() , тому ядро довільного лінійного оператора не є пустою множиною, так як воно завжди містить оператор
, тому ядро довільного лінійного оператора не є пустою множиною, так як воно завжди містить оператор ![]() .
.
Теорема 2.2. Якщо ![]() містить єдиний вектор
містить єдиний вектор ![]() , то оператор
, то оператор ![]() є взаємно-однозначним.
є взаємно-однозначним.
Доведення. Нехай ![]() - два довільно взятих вектора лінійного простору. Якщо показати, що
- два довільно взятих вектора лінійного простору. Якщо показати, що ![]() , то це буде означати, що оператор
, то це буде означати, що оператор ![]() є взаємно-однозначним. Припустимо противне, що знайдуться два вектора
є взаємно-однозначним. Припустимо противне, що знайдуться два вектора ![]() і
і ![]() , такі, що
, такі, що ![]() , а
, а ![]() . Тоді для цих векторів
. Тоді для цих векторів ![]() . За умовою теореми
. За умовою теореми ![]() складається із єдиного вектора
складається із єдиного вектора ![]() , тобто для вектора
, тобто для вектора ![]() і тільки для нього
і тільки для нього ![]() . В силу цього
. В силу цього ![]() чи
чи ![]() . Ми прийшли до протиріччя з припущенням про те, що
. Ми прийшли до протиріччя з припущенням про те, що ![]() . Тому для будь-яких не рівних один одному векторів
. Тому для будь-яких не рівних один одному векторів ![]() і
і ![]() простору
простору ![]()
![]() . Отже, твердження теореми вірне.
. Отже, твердження теореми вірне.
Теорема 2.3. Для того, щоб оператор ![]() мав обернений, необхідно і достатньо, щоб
мав обернений, необхідно і достатньо, щоб ![]() .
.
Доведення цієї теореми основується на теоремах 2.1 і 2.2 про обернений оператор і ядро взаємно-однозначного оператора.
Образом оператора ![]() називається множина
називається множина ![]() всіх векторів простору
всіх векторів простору ![]() , кожний з яких має прообраз, тобто якщо
, кожний з яких має прообраз, тобто якщо ![]() , то існує такий вектор
, то існує такий вектор ![]() , що
, що ![]() . Легко побачити, що якщо
. Легко побачити, що якщо ![]() містить тільки нульовий вектор, то
містить тільки нульовий вектор, то ![]() є весь лінійний простір
є весь лінійний простір ![]() :
: ![]() . Дійсно, якщо
. Дійсно, якщо ![]() , то оператор
, то оператор ![]() є взаємно-однозначним. За доведеною вище властивістю взаємно-однозначного оператора кожний вектор
є взаємно-однозначним. За доведеною вище властивістю взаємно-однозначного оператора кожний вектор ![]() простору
простору ![]() має єдиний прообраз
має єдиний прообраз ![]() :
: ![]() , так що
, так що ![]() .
.
Покажемо тепер, що множина ![]() для довільного лінійного простору
для довільного лінійного простору ![]() є підпростором лінійного простору
є підпростором лінійного простору ![]() . Нехай
. Нехай ![]() і
і ![]() – два довільно взятих вектори множини
– два довільно взятих вектори множини ![]() . Так як
. Так як ![]() , то
, то ![]() . Нехай
. Нехай ![]() – довільне число. Так як
– довільне число. Так як ![]() , то
, то ![]() . Таким чином, лінійні операції над будь-якими векторами множини
. Таким чином, лінійні операції над будь-якими векторами множини ![]() дають вектори тієї ж множини, тобто
дають вектори тієї ж множини, тобто ![]() – підпростір простору
– підпростір простору ![]() .
.
Аналогічним способом доводиться, що множина ![]() також є підпростором простору
також є підпростором простору ![]() .
.
Розмірність підпростору ![]() називається дефектом оператора
називається дефектом оператора![]() . Розмірність підпростору
. Розмірність підпростору ![]() називається рангом оператора
називається рангом оператора ![]() . Для рангу оператора
. Для рангу оператора ![]() використовується одне з позначень
використовується одне з позначень ![]() або
або ![]() , для позначення дефекту оператора використовується символ
, для позначення дефекту оператора використовується символ ![]() .
.
Теорема 2.4. Для будь-якого лінійного оператора ![]() із
із ![]() сума розмінностей його ядра і образу дорівнює розмірності простору
сума розмінностей його ядра і образу дорівнює розмірності простору ![]() , тобто
, тобто ![]() або
або ![]() .
.
Теорема 2.5. Нехай ![]() і
і ![]() - два яких-небудь підпростори
- два яких-небудь підпростори ![]() - мірного простору
- мірного простору ![]() , причому
, причому ![]() . Тоді існує такий лінійний оператор
. Тоді існує такий лінійний оператор ![]() , що
, що ![]() , а
, а ![]() .
.
Доведення. Нехай ![]() - розмірність підпростору
- розмірність підпростору ![]() , тобто
, тобто ![]() , а
, а ![]() – розмірність підпростору
– розмірність підпростору ![]() . За умовою теореми
. За умовою теореми ![]() . Виберемо базис
. Виберемо базис ![]()
![]() - мірного простору
- мірного простору ![]() так, щоб
так, щоб ![]() векторів
векторів ![]() було базисом підпростору
було базисом підпростору ![]() . В підпросторі
. В підпросторі ![]() візьмемо який-небудь базис
візьмемо який-небудь базис ![]() . Розглянемо лінійний оператор
. Розглянемо лінійний оператор ![]() , який перетворює вектори
, який перетворює вектори ![]() простору
простору ![]() у вектори
у вектори ![]() , а кожний з векторів
, а кожний з векторів ![]() у нульовий вектор, тобто
у нульовий вектор, тобто ![]() .
.
Оператор ![]() довільний вектор
довільний вектор ![]() простору
простору ![]() приводить у вектор
приводить у вектор ![]()
![]() , який належить підпростору
, який належить підпростору ![]() простора
простора ![]() . Звідси випливає, що
. Звідси випливає, що ![]() , тобто підпростір
, тобто підпростір ![]() містить образ оператора
містить образ оператора ![]() . Щоб довести, що
. Щоб довести, що ![]() , треба за означенням множини
, треба за означенням множини ![]() показати, що будь-який вектор
показати, що будь-який вектор ![]() підпростору
підпростору ![]() , має прообраз у просторі
, має прообраз у просторі ![]() . Розглянутий лінійний оператор
. Розглянутий лінійний оператор ![]() перетворює вектори
перетворює вектори ![]() простору
простору ![]() у вектори
у вектори ![]() , тому довільно взятий вектор
, тому довільно взятий вектор ![]() підпростору
підпростору ![]() можна представити у вигляді
можна представити у вигляді ![]() . В силу лінійності оператора и також того, що
. В силу лінійності оператора и також того, що ![]() , вектор
, вектор ![]() можна представити також і в такій формі:
можна представити також і в такій формі: ![]()
![]() , де
, де ![]() – довільно вибрані комплексні числа. Останній вираз для довільного вектору
– довільно вибрані комплексні числа. Останній вираз для довільного вектору ![]() означає, що він є образом вектора
означає, що він є образом вектора ![]() простору
простору ![]() . Таким чином,
. Таким чином, ![]() .
.
Покажемо тепер, що підпростір ![]() є ядром оператора
є ядром оператора ![]() . Нехай
. Нехай ![]() який-небудь вектор підпростору
який-небудь вектор підпростору ![]() . Так як
. Так як ![]() , то це означає, що вектор
, то це означає, що вектор ![]() входить в ядро оператора
входить в ядро оператора ![]() . Звідси випливає, що підпростір
. Звідси випливає, що підпростір ![]() . Для доведення того, що
. Для доведення того, що ![]() треба показати, що будь-який вектор
треба показати, що будь-який вектор ![]() простору
простору ![]() , що не належить підпростору
, що не належить підпростору ![]() , не може бути елементом ядра оператора
, не може бути елементом ядра оператора ![]() . Нехай
. Нехай ![]() - вектор простору
- вектор простору ![]() , який не належить підпростору
, який не належить підпростору ![]() . Зрозуміло, що хоча б одна із координат
. Зрозуміло, що хоча б одна із координат ![]() цього вектору не рівна нулю, так як в протилежному випадку
цього вектору не рівна нулю, так як в протилежному випадку ![]() . Розглянемо
. Розглянемо ![]() . Так як
. Так як ![]() лінійно незалежні вектори, а серед чисел
лінійно незалежні вектори, а серед чисел ![]() є відмінні від нуля, то
є відмінні від нуля, то ![]() . Це означає, що будь-який вектор, що не належить підпростору
. Це означає, що будь-який вектор, що не належить підпростору ![]() , не належить і ядру оператора
, не належить і ядру оператора ![]() . Отже,
. Отже, ![]() .
.
Теорема 2.6. Нехай ![]() і
і ![]() – два яких-небудь лінійних оператора із множини
– два яких-небудь лінійних оператора із множини ![]() , тоді
, тоді ![]() ,
, ![]() .
.
Доведення. Нехай ![]() – довільний вектор простору
– довільний вектор простору ![]() . Зрозуміло, що
. Зрозуміло, що ![]() . Будь-який вектор
. Будь-який вектор ![]() множини
множини ![]() за означенням добутку операторів це вектор
за означенням добутку операторів це вектор ![]() . Останній є вектором множини
. Останній є вектором множини ![]() . З цього слідує, що має місце включення
. З цього слідує, що має місце включення ![]() . А це означає, що
. А це означає, що ![]() , тобто
, тобто ![]() . Перше твердження теореми доведено.
. Перше твердження теореми доведено.
Доведемо справедливість другого. Нехай ![]() – довільний вектор ядра оператора
– довільний вектор ядра оператора ![]() , тоді
, тоді ![]() , і, тому,
, і, тому, ![]() . Це означає, що якщо
. Це означає, що якщо ![]() , то
, то ![]() , тобто
, тобто ![]() . Звідси випливає нерівність
. Звідси випливає нерівність ![]() . Позначимо через
. Позначимо через ![]() розмірність простору
розмірність простору ![]() . Згідно теореми 2.4
. Згідно теореми 2.4 ![]() ,
, ![]() . Так як
. Так як ![]() , то
, то ![]() , тобто
, тобто ![]() .
.
Теорема 2.7. Нехай ![]() – розмірність простору
– розмірність простору ![]() ,
, ![]() і
і ![]() – лінійні оператори із
– лінійні оператори із ![]() , тоді
, тоді ![]() .
.
Похожие работы
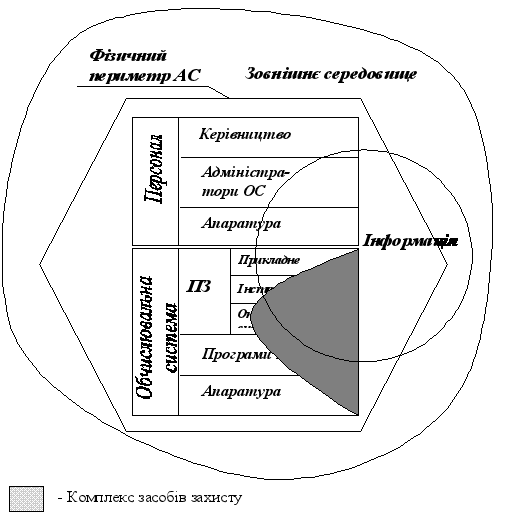
... В АБС АКБ «ПРОМІНВЕСТБАНК» ТА ОЦІНКА РІВНЯ ВРАЗЛИВОСТІ БАНКІВСЬКОЇ ІНФОРМАЦІЇ 3.1 Постановка алгоритму задачі формування та опис елементів матриці контролю комплексної системи захисту інформації (КСЗІ) інформаційних об’єктів комерційного банку В дипломному дослідженні матриця контролю стану побудови та експлуатації комплексної системи захисту інформації в комерційному банку представлена у вигляді ...
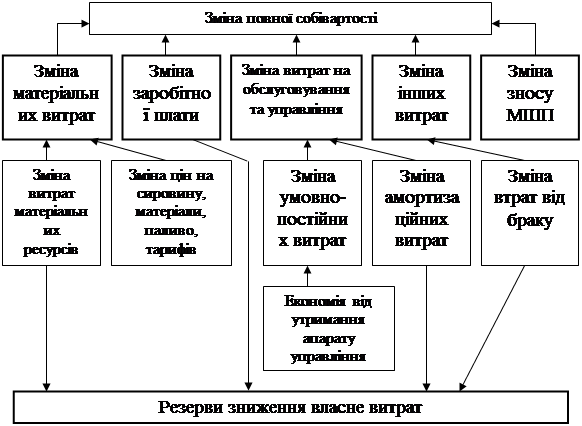
... і над плановим. Відомо, що собівартість є одним з головних джерел резервів підвищення ефективності роботи підприємства. Звідси сформуємо мету і задачі даної роботи. Метою даної роботи є підвищення ефективності роботи підприємства ВАТ «Дніпрополімермаш» шляхом управління собівартістю продукції. Відповідно, для досягнення поставленої мети необхідно вирішити наступні задачі: 1. Проаналізувати ...
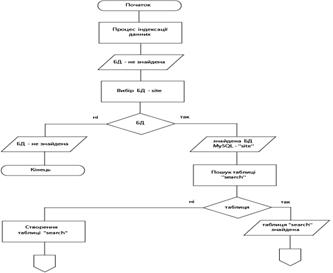
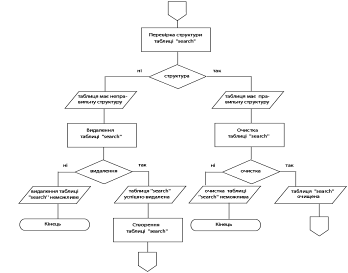
... в даній роботі, була опробована й досліджена в реальних умовах моєї професійної діяльності й показала свою працездатність і ефективність. 3. Розробка системи керування та актуалізації інформації web-сайту національного оператора Енергоринка 3.1 Вибір інструментарію для створення web-сайту та системи керування Перед тим, як безпосередньо перейти до створення Web-сайту Національного ...
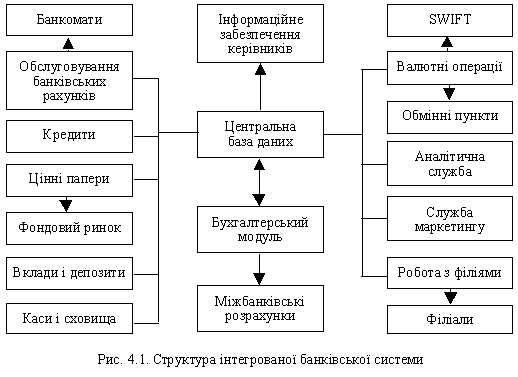
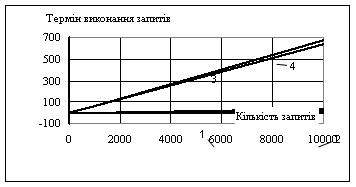
... маржі В такому випадку, макимізація прибутку відбувається за рахунок швидкого обороту коштів. Запропонований метод було прийнято як альтернативний метод визначення умов надання банківських послуг в Дніпропетровській філії АБ "Правексбанк", що дозволило збільшити фінансовий результат за перші 5 місяців 2008 року на 6 процентів. 4. АВТОМАТИЗОВАНА ІНФОРМАЦІЙНА СИСТЕМА Рис. 4.1 – Блок- ...


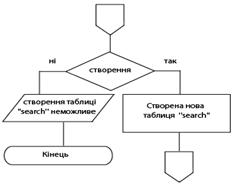
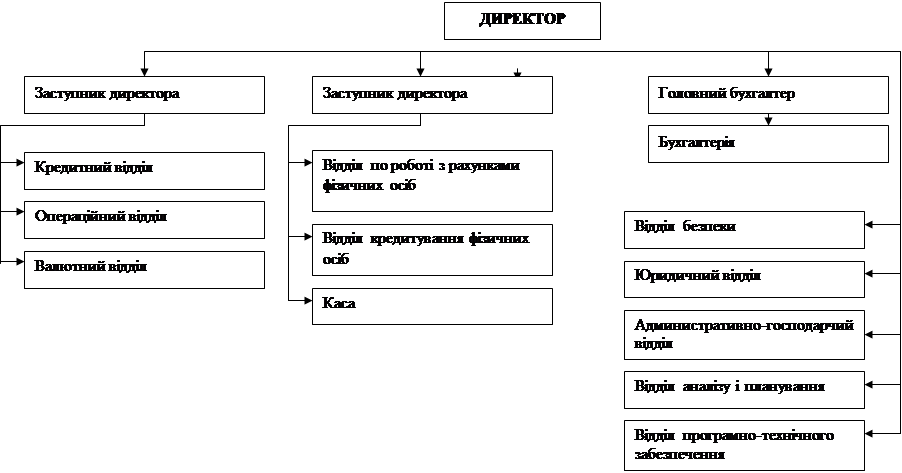
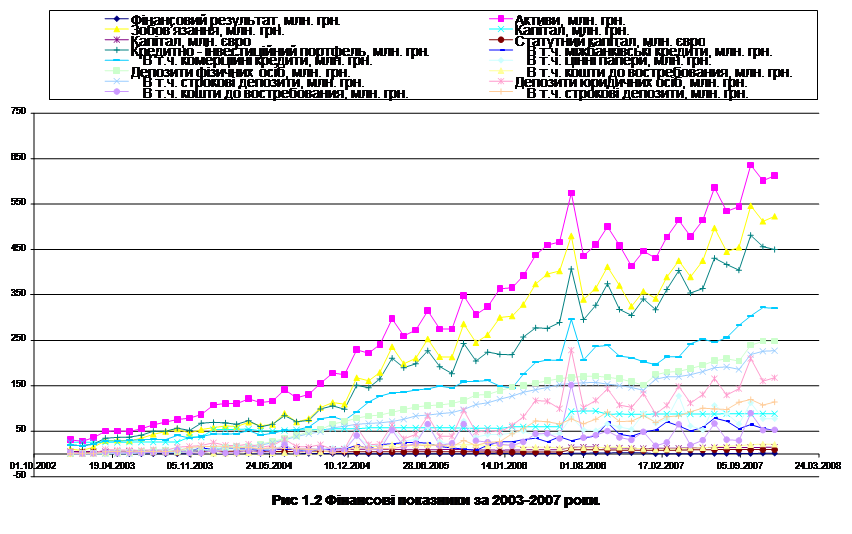
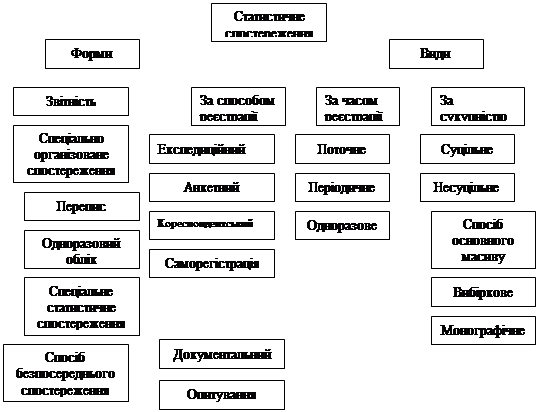
0 комментариев