Навигация
Власні значення і власні вектори оператора
5. Власні значення і власні вектори оператора
Число ![]() називається власним числом лінійного оператора
називається власним числом лінійного оператора ![]() , якщо у просторі
, якщо у просторі ![]() можна знайти такий ненульовий вектор
можна знайти такий ненульовий вектор ![]() , що
, що
![]() (5.1)
(5.1)
Будь-який ненульовий вектор, задовольняючий рівності (5.1), називають власним вектором оператора ![]() , що відповідає власному значенню
, що відповідає власному значенню ![]() .
.
Рівність (5.1) можна записати по іншому ![]() , де
, де ![]() – тотожний оператор. Оскільки
– тотожний оператор. Оскільки ![]() – ненульовий вектор, то зрозуміло, що розмірність ядра оператора
– ненульовий вектор, то зрозуміло, що розмірність ядра оператора ![]() не менше одиниці. Нехай
не менше одиниці. Нехай ![]() – розмірність простору
– розмірність простору ![]() , в якому діє оператор
, в якому діє оператор ![]() . Відомо, що
. Відомо, що ![]() . Звісно,
. Звісно,
![]() . Але тоді
. Але тоді ![]() .
.
Таким чином, якщо число ![]() є власним значенням оператора
є власним значенням оператора ![]() , то
, то ![]() є коренем рівняння
є коренем рівняння ![]() (характеристичне рівняння або вікове рівняння оператора
(характеристичне рівняння або вікове рівняння оператора ![]() ).
).
Вияснимо, чи всі корені характеристичного рівняння ![]() будуть власними значеннями оператора
будуть власними значеннями оператора ![]() . Нехай
. Нехай ![]() – який-небудь корінь рівняння, тоді для цього значення
– який-небудь корінь рівняння, тоді для цього значення ![]()
![]() . Це означає, що матриця оператора
. Це означає, що матриця оператора ![]() буде виродженою у будь-якому базисі простору
буде виродженою у будь-якому базисі простору ![]() . Як наслідок,
. Як наслідок, ![]() . Так як
. Так як ![]() , то
, то ![]() . А це означає, що існую по меншій мірі один ненульовий вектор
. А це означає, що існую по меншій мірі один ненульовий вектор ![]() , такий, що
, такий, що ![]() чи
чи ![]() . Таким чином, будь-який корінь характеристичного рівняння
. Таким чином, будь-який корінь характеристичного рівняння ![]() буде власним значенням оператора
буде власним значенням оператора ![]() , тобто вірне твердження.
, тобто вірне твердження.
Теорема 5.1. Для того, щоб комплексне число ![]() було власним значенням лінійного оператора
було власним значенням лінійного оператора ![]() , необхідно і достатньо, щоб це число було коренем характеристичного рівняння
, необхідно і достатньо, щоб це число було коренем характеристичного рівняння ![]() .
.
Нехай ![]() – базис простору
– базис простору ![]() и нехай
и нехай
 ,
,
матриця лінійного оператора ![]() у цьому базисі. Відомо, що матриця тотожного оператора
у цьому базисі. Відомо, що матриця тотожного оператора ![]() в будь-якому базисі буде одиничною, тому в розглянутому базисі простору
в будь-якому базисі буде одиничною, тому в розглянутому базисі простору ![]() оператор
оператор ![]() характеризується такою матрицею
характеризується такою матрицею
 .
.
Визначник цієї матриці, тобто ![]() , називається характеристичним або віковим визначником оператора
, називається характеристичним або віковим визначником оператора ![]() . Легко побачити, що добуток елементів
. Легко побачити, що добуток елементів ![]() головної діагоналі вікового визначника буде многочленом степені
головної діагоналі вікового визначника буде многочленом степені ![]() , решта членів визначника будуть многочленами степені не вище
, решта членів визначника будуть многочленами степені не вище ![]() . З цього видно, що віковий визначник оператора
. З цього видно, що віковий визначник оператора ![]() є многочленом степені
є многочленом степені ![]() . За наслідком з основної теореми алгебри такий многочлен має
. За наслідком з основної теореми алгебри такий многочлен має ![]() коренів, якщо кожний корінь рахувати стільки разів, яка його кратність. Тому число власних значень оператора
коренів, якщо кожний корінь рахувати стільки разів, яка його кратність. Тому число власних значень оператора ![]() , діючого в
, діючого в ![]() -мірному просторі, дорівнює
-мірному просторі, дорівнює ![]() , якщо кожне власне значення рахувати стільки разів, яка його кратність.
, якщо кожне власне значення рахувати стільки разів, яка його кратність.
Відомо, що в різних базисах простору ![]() матриці оператора
матриці оператора ![]() , взагалі-то, різні. У зв’язку з цим виникає питання про пошук такого базису простору
, взагалі-то, різні. У зв’язку з цим виникає питання про пошук такого базису простору ![]() , в якому матриця оператора має найпростіший вигляд (найбільше число нульових елементів). Припустімо, що у просторі
, в якому матриця оператора має найпростіший вигляд (найбільше число нульових елементів). Припустімо, що у просторі ![]() існує базис
існує базис ![]() всі вектори якого є власними векторами оператора
всі вектори якого є власними векторами оператора ![]() , тобто
, тобто ![]()
![]() . У цьому базисі матриця оператора буде мати діагональний вигляд
. У цьому базисі матриця оператора буде мати діагональний вигляд
 .
.
Навпаки, якщо в якому-небудь базисі простору ![]() матриця лінійного оператора
матриця лінійного оператора ![]() має діагональний вид, то всі вектори базису є власними векторами оператора
має діагональний вид, то всі вектори базису є власними векторами оператора ![]() . Таким чином, доведено наступне твердження.
. Таким чином, доведено наступне твердження.
Теорема 5.2. Для того, щоб матриця лінійного оператора ![]() у базисі
у базисі ![]() простору
простору ![]() була діагональною, необхідно і достатньо, щоб вектори
була діагональною, необхідно і достатньо, щоб вектори ![]() були власними векторами оператора
були власними векторами оператора ![]() . Теорема 5.3. Якщо власні значення
. Теорема 5.3. Якщо власні значення ![]() лінійного оператора
лінійного оператора ![]() , діючого в
, діючого в ![]() -мірному просторі
-мірному просторі ![]() , різні, тоді відповідні їм власні вектори
, різні, тоді відповідні їм власні вектори ![]() лінійно незалежні.
лінійно незалежні.
Наслідок. Якщо характеристичне рівняння ![]() має
має ![]() різних коренів, то у
різних коренів, то у ![]() -мірному векторному просторі існує базис, в якому матриця оператора
-мірному векторному просторі існує базис, в якому матриця оператора ![]() має діагональний вид.
має діагональний вид.
Якщо оператор ![]() має кратні власні значення, то може виявитися, що максимальна лінійно незалежна сукупність власних векторів оператора
має кратні власні значення, то може виявитися, що максимальна лінійно незалежна сукупність власних векторів оператора ![]() не буда утворювати базис лінійного простору, в якому діє оператор
не буда утворювати базис лінійного простору, в якому діє оператор ![]() . У зв’язку з цим виникає питання, якими векторами доповнити до базису простору максимальну лінійно незалежну сукупність власних векторів, щоб у цьому базисі матриця мала найпростіший вигляд. Відповідь на це питання дав французький математик Жордан.
. У зв’язку з цим виникає питання, якими векторами доповнити до базису простору максимальну лінійно незалежну сукупність власних векторів, щоб у цьому базисі матриця мала найпростіший вигляд. Відповідь на це питання дав французький математик Жордан.
Вектор ![]() називається приєднаним вектором оператора
називається приєднаним вектором оператора ![]() , що відповідає кратному власному значенню
, що відповідає кратному власному значенню ![]() цього оператора, якщо можна вказати таке натуральне число
цього оператора, якщо можна вказати таке натуральне число ![]() , що
, що ![]() . Число
. Число ![]() називається порядком приєднаного вектора
називається порядком приєднаного вектора ![]() . Нехай
. Нехай ![]() – приєднаний вектор порядку
– приєднаний вектор порядку ![]() , що відповідає власному значенню
, що відповідає власному значенню ![]() . Позначимо через
. Позначимо через ![]() вектор
вектор ![]() . Тоді за означенням приєднаного вектора
. Тоді за означенням приєднаного вектора ![]() або
або ![]() . Вектор
. Вектор ![]() виявляється власним вектором оператора
виявляється власним вектором оператора ![]() . Цю властивість приєднаного вектора можна використовувати при побудові приєднаних векторів за заданим власним вектором
. Цю властивість приєднаного вектора можна використовувати при побудові приєднаних векторів за заданим власним вектором ![]() .
.
Теорема 5.4. (теорема Жордана). У ![]() -мірному векторному просторі
-мірному векторному просторі ![]() існує базис
існує базис ![]() , побудований із
, побудований із ![]() власних векторів
власних векторів ![]() і відповідних їм приєднаних векторів, такий, що
і відповідних їм приєднаних векторів, такий, що
![]() ,
, ![]() ;
; ![]() ,
, ![]() .
.
У цьому базисі матриця оператора ![]() має наступний вид
має наступний вид
 ,
,
де ![]() - квадратна матриця порядку
- квадратна матриця порядку ![]() (клітка Жордана):
(клітка Жордана):
 .
.
Вказана в теоремі 5.4 форма матриці ![]() оператора
оператора ![]() називається жордановою або канонічною формою матриці цього оператора.
називається жордановою або канонічною формою матриці цього оператора.
На кінець відмітимо, що якщо ![]() – власний вектор лінійного оператора
– власний вектор лінійного оператора ![]() , то і вектор
, то і вектор ![]() , де
, де ![]() – довільно взяте відмінне від нуля число, також буде власним вектором оператора
– довільно взяте відмінне від нуля число, також буде власним вектором оператора ![]() . Дійсно,
. Дійсно,
![]() .
.
Приклад 1. З’ясувати, які з перетворень ![]() , заданих шляхом завдання координат вектора
, заданих шляхом завдання координат вектора ![]() як функцій координат вектора
як функцій координат вектора ![]() , являються лінійними, і в випадку лінійності знайти їх матриці в тому базисі, в якому задано координати векторів
, являються лінійними, і в випадку лінійності знайти їх матриці в тому базисі, в якому задано координати векторів ![]() і
і ![]() .
.
![]() .
.
Розв’язання: Для того, щоб дізнатись, чи являються лінійними функції координат вектора треба перевірити, чи виконуються наступні дві аксіоми:
Аксіома адитивності: ![]() .
.
Для будь-яких векторів ![]() та
та ![]() повинно виконуватись
повинно виконуватись
![]() .
.
![]()
![]()
![]()
![]()
![]() .
.
Аксіома адитивності виконується.
Перевіримо аксіому однорідності:
![]()
![]()
![]()
![]()
![]()
Так як властивість адитивності і однорідності виконується, тому перетворення ![]() – лінійне.
– лінійне.
Приклад 2. З’ясувати, які з перетворень ![]() , заданих шляхом завдання координат вектора
, заданих шляхом завдання координат вектора ![]() як функцій координат вектора
як функцій координат вектора ![]() , являються лінійними, і в випадку лінійності знайти їх матриці в тому базисі, в якому задано координати векторів
, являються лінійними, і в випадку лінійності знайти їх матриці в тому базисі, в якому задано координати векторів ![]() і
і ![]() .
.
![]() .
.
Розв’язання: Для того, щоб дізнатись, чи являються лінійними функції координат вектора треба перевірити, чи виконуються наступні дві аксіоми:
Аксіома адитивності: ![]() .
.
Для будь-яких векторів ![]() та
та ![]() повинно виконуватись
повинно виконуватись
![]()
![]()
![]()
![]()
![]() .
.
Так як властивість адитивності не виконується, тому перетворення ![]() – не лінійне.
– не лінійне.
Приклад 3. Показати, що множення квадратних матриць другого порядку а) зліва, б) з права на дану матрицю 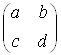 являються лінійними перетвореннями простору всіх матриць другого порядку, і знайти матриці їх перетворень в базисі, який складається з матриць:
являються лінійними перетвореннями простору всіх матриць другого порядку, і знайти матриці їх перетворень в базисі, який складається з матриць:
 ,
, 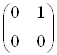 ,
, 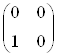 ,
, 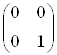
Розв’язання: За означенням матриці лінійного перетворення ![]() ,
,  . Знаходимо образи базисних векторів і обчислюємо їх координати в заданому базисі:
. Знаходимо образи базисних векторів і обчислюємо їх координати в заданому базисі:
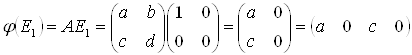
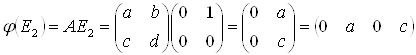
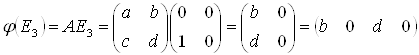
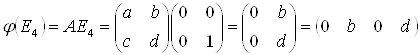
Розташувавши отримані координати образів за стовпчиками отримаємо матрицю лінійного перетворення:
 .
.
Приклад 4. Лінійне перетворення ![]() в базисі
в базисі ![]() має матрицю
має матрицю
A=
Знайти матрицю цього ж перетворення в базисі: e![]() ,
, ![]() ,
, ![]() ,
, ![]() +
+![]() .
.
Розв’язання: Формула зв’язку між векторами старого і нового базисів у матричному записі має вигляд:
![]()
Обернену матрицю знайдемо за допомогою приєднаної:

Підставляємо отримані значення в формулу, отримаємо:
 .
.
Приклад 5. Знайти власні значення і власні вектори лінійного перетворення, заданому в деякому базисі матрицею:  .
.
Розв’язання: Складаємо характеристичне рівняння і розв’язавши його знаходимо власні числа:
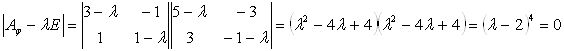
Розв’язуємо її методом Гауса, для цього приводимо матрицю до східчастого вигляду:

![]()
Складаємо однорідну систему рівнянь для визначення власних векторів:

![]()
Оскільки максимальна кількість лінійно незалежних власних векторів менша за вимірність простору, то власні вектори не утворюють базис простору і таким чином матриця не діагоналізуєма.![]()
Приклад 6. З’ясувати, яку з матриць лінійних перетворень можна привести до діагонального виду шляхом переходу до нового базису. Знайти цей базис і відповідну йому матрицю: 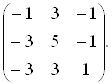
Розв’язання: Складаємо характеристичне рівняння і розв’язавши його знаходимо власні числа:
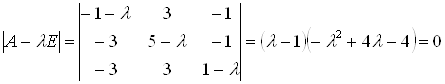
![]()
Розв’язуємо її методом Гауса, для цього приводимо матрицю до східчастого вигляду:
A=
Власні вектори мають вигляд: ![]() .
. ![]()
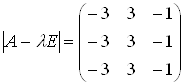
![]() ,
, ![]()
Формула зв’язку між векторами старого і нового базисів у матричному записі має вигляд:
![]()
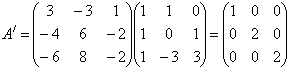 .
.
Матриця діагоналізована.
Приклад 7. З’ясувати, яку з матриць лінійних перетворень можна привести до діагонального виду шляхом переходу до нового базису. Знайти цей базис і відповідну йому матрицю: 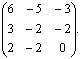
Розв’язання: Складаємо характеристичне рівняння і розв’язавши його знаходимо власні числа:
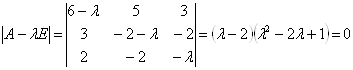
![]()
Розв’язуємо її методом Гауса, для цього приводимо матрицю до східчастого вигляду:
A=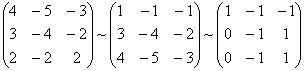
![]()
A=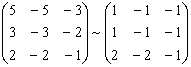
Матриця не може бути діагоналізованою, так як а.к.=г.к.=1.
Висновки
В даній курсовій роботі розглянуто базові властивості лінійних операторів, поняття матриці лінійного оператора та питання зв’язку матриць оператора у різних базисах. Крім того, до роботи включені питання діагоналізіруємості матриці оператора, які пов’язані з існуванням базису, що складається з власних векторів оператора. За усіма розглянутими теоретичними питаннями зроблена підборка задач, яка їх ілюструє та допомагає детально розібратися в теоретичному матеріалі.
оператор вектор лінійний матриця базис
Перелік посилань
1. Курош А.Г. Курс вищої алгебри. – М.: Наука, 1968. – 331 с.
2. Кострикін А.И., Манін Ю.И. Лінійна алгебра і геометрія. – М.: Наука, 1986. – 304 с.
3. Проскуряков І. В. Збірник задач з лінійної алгебри. – М.: Наука, 1974. – 384 с.
Похожие работы
... В АБС АКБ «ПРОМІНВЕСТБАНК» ТА ОЦІНКА РІВНЯ ВРАЗЛИВОСТІ БАНКІВСЬКОЇ ІНФОРМАЦІЇ 3.1 Постановка алгоритму задачі формування та опис елементів матриці контролю комплексної системи захисту інформації (КСЗІ) інформаційних об’єктів комерційного банку В дипломному дослідженні матриця контролю стану побудови та експлуатації комплексної системи захисту інформації в комерційному банку представлена у вигляді ...
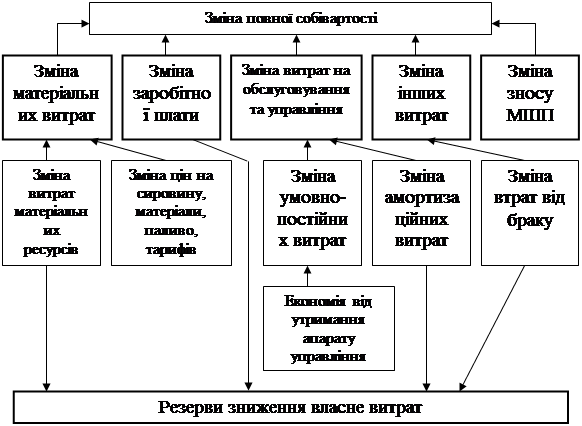
... і над плановим. Відомо, що собівартість є одним з головних джерел резервів підвищення ефективності роботи підприємства. Звідси сформуємо мету і задачі даної роботи. Метою даної роботи є підвищення ефективності роботи підприємства ВАТ «Дніпрополімермаш» шляхом управління собівартістю продукції. Відповідно, для досягнення поставленої мети необхідно вирішити наступні задачі: 1. Проаналізувати ...
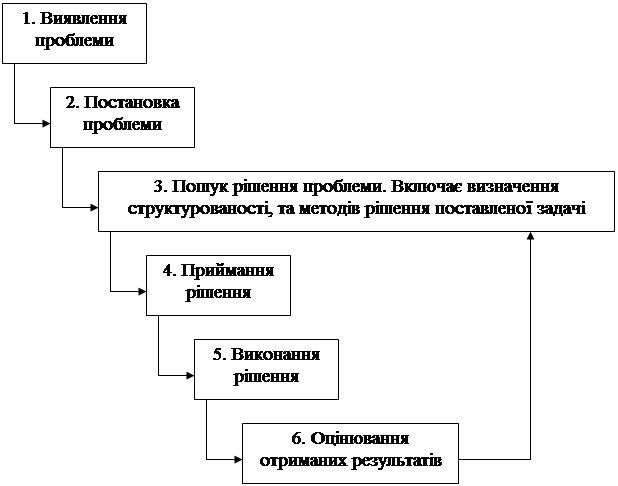
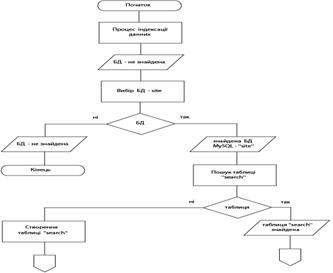
... в даній роботі, була опробована й досліджена в реальних умовах моєї професійної діяльності й показала свою працездатність і ефективність. 3. Розробка системи керування та актуалізації інформації web-сайту національного оператора Енергоринка 3.1 Вибір інструментарію для створення web-сайту та системи керування Перед тим, як безпосередньо перейти до створення Web-сайту Національного ...
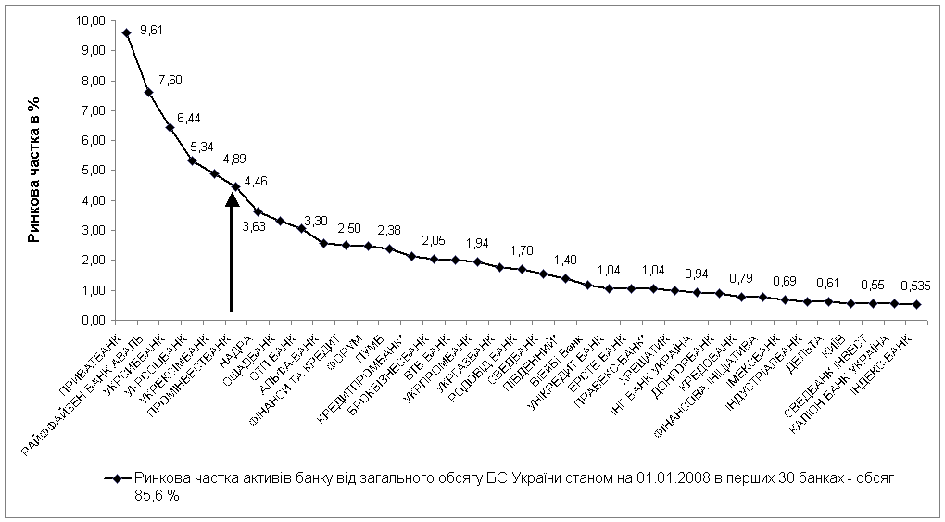
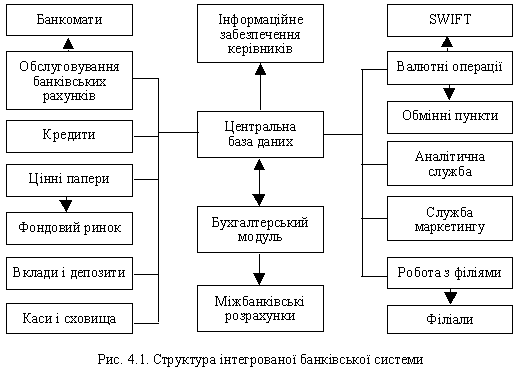
... маржі В такому випадку, макимізація прибутку відбувається за рахунок швидкого обороту коштів. Запропонований метод було прийнято як альтернативний метод визначення умов надання банківських послуг в Дніпропетровській філії АБ "Правексбанк", що дозволило збільшити фінансовий результат за перші 5 місяців 2008 року на 6 процентів. 4. АВТОМАТИЗОВАНА ІНФОРМАЦІЙНА СИСТЕМА Рис. 4.1 – Блок- ...


0 комментариев