Навигация
Матриця лінійного оператора
26324
знака
0
таблиц
5
изображений
3. Матриця лінійного оператора
Нехай 
- деякий базис лінійного простору 
, а 
– який-небудь лінійний оператор, діючий із в . Вектор 
оператор перетворює в вектор 
. Вектори 
простору розкладемо по векторах базису цього простору. Побудуємо матрицю 
порядку 
, стовпці якої складені із координат векторів ,
, 
, 
.
Матриця називається матрицею оператора в базисі 
.
Приклад. Записати матрицю тотожного і нульового операторів у базисі простору .
Розв’язок. Тотожний оператор 
будь-який вектор простору приводить в той же самий оператор. Тому 
. А це означає, що матриця 
тотожного оператора буде одиничною в будь-якому базисі простору . Нульовий оператор 
будь-який вектор простору перетворює в нульовий вектор, тому матриця 
цього оператора – нульова в будь-якому базисі.
Із сказаного вище випливає, що в обраному базисі -мірного простору з кожним лінійним оператором 
можна зв’язати квадратну матрицю порядку . Виникає питання: чи можна кожній квадратній матриці порядку поставити у відповідність такий лінійний оператор , матриця якого в заданому базисі 
простору співпадає з матрицею ? Стверджувальну відповідь на це питання дає
Теорема 3.1. Нехай 
– деяка квадратна матриця порядку . Нехай – довільний обраний базис -мірного лінійного простору . Тоді існує єдиний лінійний оператор 
, який у вказаному базисі має матрицю .
Доведення. Розглянемо лінійний оператор , який вектори базису простору перетворює у вектори 
, 
. У базисі оператор , очевидно, має матрицю . Залишається довести, що є єдиним оператором з матрицею. Припустимо протилежне, що, крім оператора , існує ще лінійний оператор 
, маючий матрицю в базисі . Це означає, що 
, . Виберемо який-небудь вектор 
простору і розглянемо вектори 
і 
. Маємо 
.
Як наслідок, що для будь-якого 
. Звідси витікає, що 
. Теорему доведено.
Теорема 3.2. Нехай – матриця лінійного оператора в базисі простору . Ранг оператора дорівнює рангу його матриці: 
.
Доведення. В основі доведення лежать означення рангу оператора і рангу матриці: 
, ранг матриці дорівнює рангу системи його стовпців.
Нехай 
– який-небудь вектор - мірного простору . Образом вектора 
є вектор 
. Як бачимо, довільний вектор образу оператора , тобто множини 
, представляє собою лінійну комбінацію векторів . Отже, 
є лінійною оболонкою множини векторів . Відомо, що розмірність лінійної оболонки дорівнює рангові системи векторів, які вони утворюють, тому 
. За означенням у стовпцях матриці оператора розміщені координати векторів у базисі . Отже, на основі означення рангу матриці 
. Таким чином, 
.
Нехай і 
матриці операторів і 
в якому-небудь базисі простору , тоді із способу побудови цих матриць витікає, що матриці операторів 
і 
, де 
і 
– довільно взяті числа, рівні відповідно 
і 
. Доведемо справедливість першого твердження, як більш складного. Дійсно, стовпці матриці оператора побудовані із координат векторів 
у базисі простору . Визначимо елементи 
-го стовпця цієї матриці, тобто координати вектора 
. Маємо
Звідси видно, що довільний елемент 
матриці 
оператора 
дорівнює 
, тобто дорівнює сумі добутків елементів 
-го рядка матриці на відповідний елемент -го стовпця матриці 
. А це означає, що 
. Твердження доведено.
Із доведеного твердження і теорем 2.6, 2.7 про ранг оператора слідує справедливість таких нерівностей для двох добутків квадратних матриць і одного порядку .
, 
,
Відомо, що необхідною і достатньою умовою існування оберненого оператора для оператора , є умова 
, де – розмірність простору . Із теореми 3.2 витікає, що остання умова еквівалентна вимозі: матриця оператора повинна бути не виродженою.
Іншими словами, щоб оператор мав обернений необхідно і достатньо, щоб його матриця в якому-небудь базисі лінійного простору виявилась не виродженою.
Похожие работы
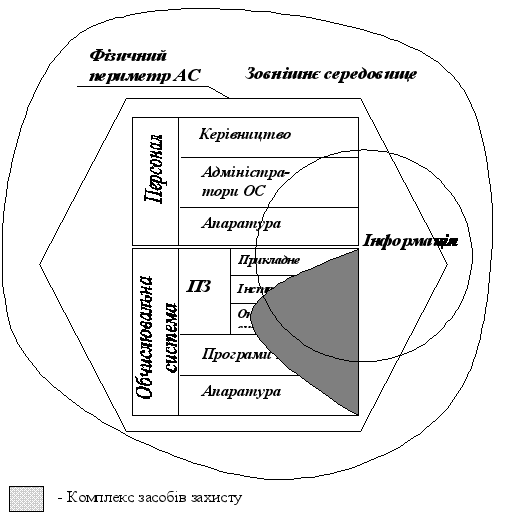
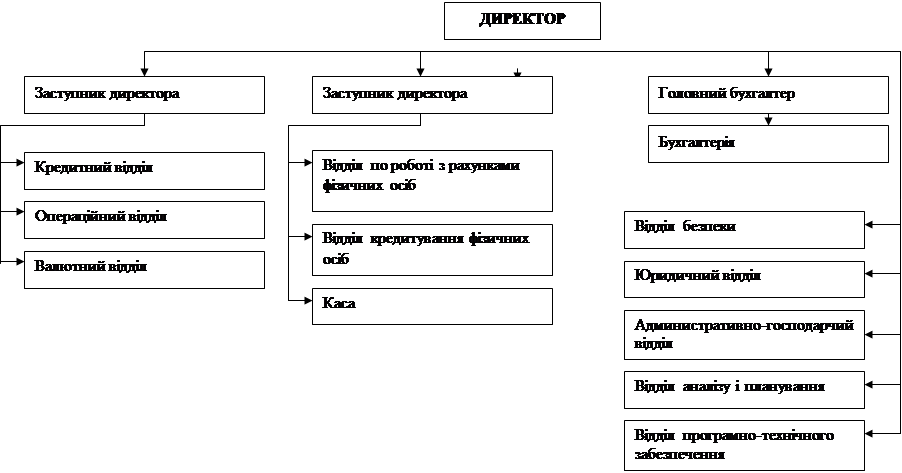
... В АБС АКБ «ПРОМІНВЕСТБАНК» ТА ОЦІНКА РІВНЯ ВРАЗЛИВОСТІ БАНКІВСЬКОЇ ІНФОРМАЦІЇ 3.1 Постановка алгоритму задачі формування та опис елементів матриці контролю комплексної системи захисту інформації (КСЗІ) інформаційних об’єктів комерційного банку В дипломному дослідженні матриця контролю стану побудови та експлуатації комплексної системи захисту інформації в комерційному банку представлена у вигляді ...
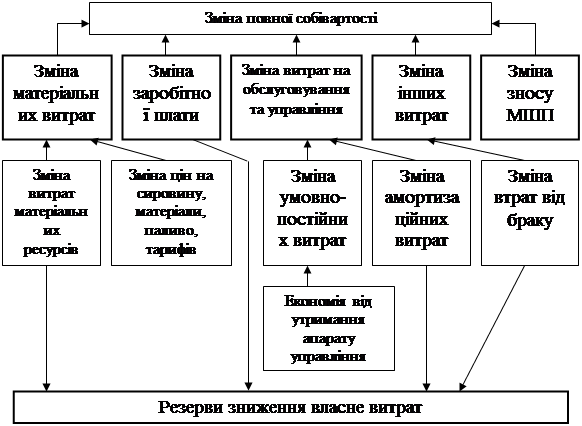
... і над плановим. Відомо, що собівартість є одним з головних джерел резервів підвищення ефективності роботи підприємства. Звідси сформуємо мету і задачі даної роботи. Метою даної роботи є підвищення ефективності роботи підприємства ВАТ «Дніпрополімермаш» шляхом управління собівартістю продукції. Відповідно, для досягнення поставленої мети необхідно вирішити наступні задачі: 1. Проаналізувати ...
... в даній роботі, була опробована й досліджена в реальних умовах моєї професійної діяльності й показала свою працездатність і ефективність. 3. Розробка системи керування та актуалізації інформації web-сайту національного оператора Енергоринка 3.1 Вибір інструментарію для створення web-сайту та системи керування Перед тим, як безпосередньо перейти до створення Web-сайту Національного ...
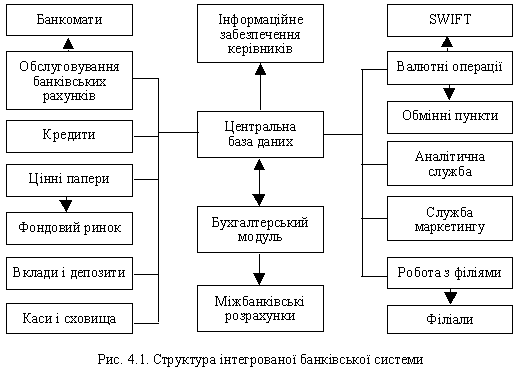
... маржі В такому випадку, макимізація прибутку відбувається за рахунок швидкого обороту коштів. Запропонований метод було прийнято як альтернативний метод визначення умов надання банківських послуг в Дніпропетровській філії АБ "Правексбанк", що дозволило збільшити фінансовий результат за перші 5 місяців 2008 року на 6 процентів. 4. АВТОМАТИЗОВАНА ІНФОРМАЦІЙНА СИСТЕМА Рис. 4.1 – Блок- ...
0 комментариев