Навигация
Перетворення матриці оператора при заміні базису
4. Перетворення матриці оператора при заміні базису
Нехай у просторі ![]() обрані два базиси
обрані два базиси ![]() і
і ![]() . Перший базис для зручності назвемо старим, а другий – новим. Координати векторів
. Перший базис для зручності назвемо старим, а другий – новим. Координати векторів ![]() у старому базисі розмістимо у стовпцях матриці
у старому базисі розмістимо у стовпцях матриці
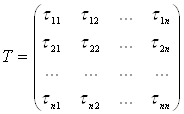 .
.
Побудована матриця називається матрицею переходу від старого базису до нового. Вектори ![]() лінійно незалежні, тому
лінійно незалежні, тому ![]() і, звісно, матриця
і, звісно, матриця ![]() не вироджена.
не вироджена.
Згідно сказаному
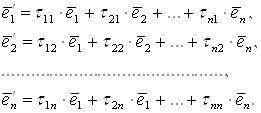
![]() (4.1)
(4.1)
Ці формули зв’язку між векторами старого і нового базисів у матричному записі мають вигляд
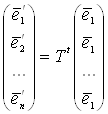 ,
,
де ![]() – транспонована матриця
– транспонована матриця ![]() .
.
Теорема 4.1. Матриці ![]() і
і ![]() оператора
оператора ![]() в базисах
в базисах ![]() і
і ![]() зв’язані співвідношеннями
зв’язані співвідношеннями
![]() ,
,
![]() ,
,
де ![]() – матриця переходу від старого базису
– матриця переходу від старого базису ![]() до нового
до нового ![]() .
.
Доведення. За означенням матриці оператора
![]() ,
,
![]()
де ![]() і
і ![]() – елементи матриць
– елементи матриць ![]() і
і ![]() . Замінимо в останній рівності вектори
. Замінимо в останній рівності вектори ![]() згідно формулам (4.1), отримаємо
згідно формулам (4.1), отримаємо
![]() (4.2)
(4.2)
З іншого боку
![]()
![]()
Але
![]()
Тому
![]() (4.3)
(4.3)
Із двох отриманих виразів (4.2) і (4.3) для вектора виходить, що
![]()
![]()
![]()
У цій рівності вектори ![]() лінійно незалежні, тому коефіцієнти про однакових векторах у лівій і правій частинах рівності мають бути однаковими, отже,
лінійно незалежні, тому коефіцієнти про однакових векторах у лівій і правій частинах рівності мають бути однаковими, отже,
![]() ,
, ![]()
Згідно означенню добутку двох матриць звідси витікає матричне рівність ![]() . Якщо помножити обидві частини цієї рівності на
. Якщо помножити обидві частини цієї рівності на ![]() праворуч, то отримаємо
праворуч, то отримаємо ![]() , якщо помножити на
, якщо помножити на ![]() злів, то будемо мати
злів, то будемо мати ![]() . Теорему доведено.
. Теорему доведено.
Матриці ![]() і
і ![]() одного й того ж порядку називаються подібними, якщо можна знайти таку не вироджену матрицю
одного й того ж порядку називаються подібними, якщо можна знайти таку не вироджену матрицю ![]() того ж порядку, що
того ж порядку, що ![]() . Із цього означення і теореми 4.1 витікає, що матриці оператора
. Із цього означення і теореми 4.1 витікає, що матриці оператора ![]() у різних базисах виявляються побідними. Покажемо, що визначники подібних матриць
у різних базисах виявляються побідними. Покажемо, що визначники подібних матриць ![]() і
і ![]() рівні. Дійсно, згадавши, що визначник добутку квадратних матриць дорівнює добутку визначників співмножників, можемо записати
рівні. Дійсно, згадавши, що визначник добутку квадратних матриць дорівнює добутку визначників співмножників, можемо записати
![]() .
.
Із доведеного твердження виходить, що визначник матриці оператора не змінюється при заміні базису. У зв’язку з цим доречно ввести поняття визначника оператора. Визначником оператора ![]() називають число
називають число ![]() , рівне визначнику матриці оператора
, рівне визначнику матриці оператора ![]() в якому-небудь базисі простору.
в якому-небудь базисі простору.
Приклад. Лінійний оператор ![]() діє на вектори базису
діє на вектори базису ![]() наступним чином:
наступним чином: ![]() . Знайти визначник оператора
. Знайти визначник оператора ![]() .
.
Розв’язок. Матриця оператора ![]() у базисі
у базисі ![]() має вигляд
має вигляд
 ,
,
тобто є верхньою трикутною. Визначник цієї матриці дорівнює одиниці, тому і ![]() .
.
Похожие работы
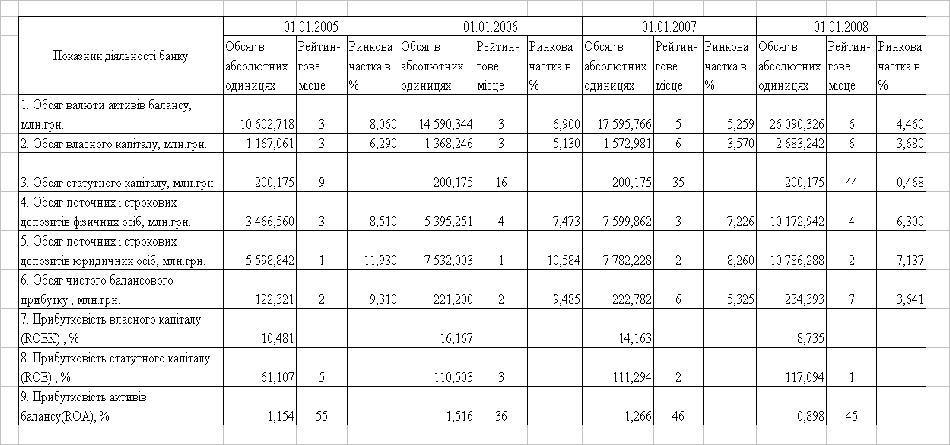
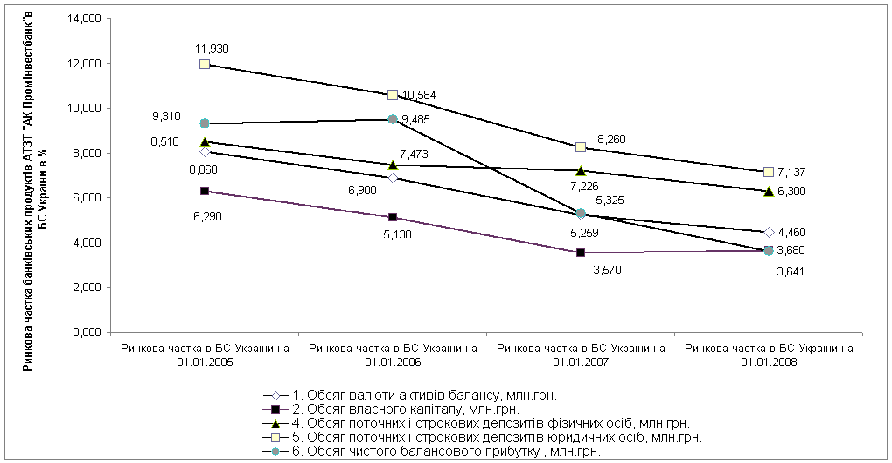
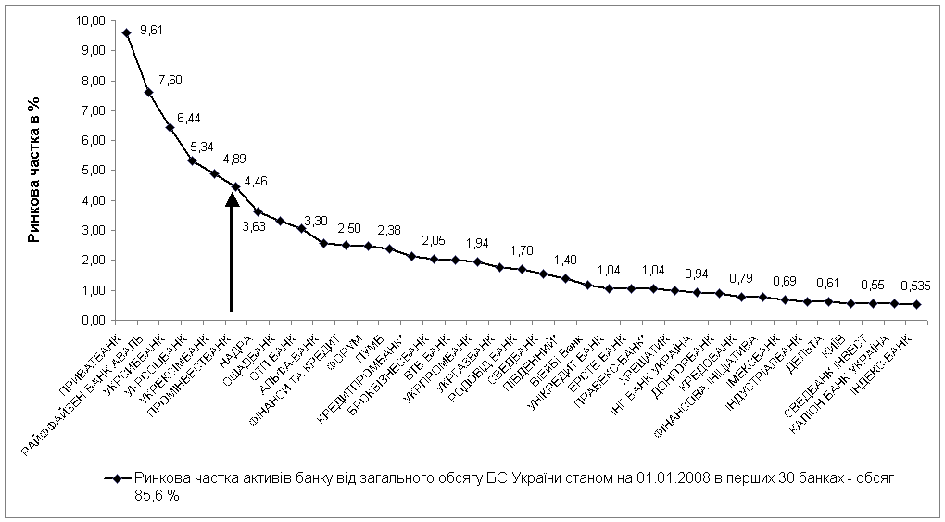
... В АБС АКБ «ПРОМІНВЕСТБАНК» ТА ОЦІНКА РІВНЯ ВРАЗЛИВОСТІ БАНКІВСЬКОЇ ІНФОРМАЦІЇ 3.1 Постановка алгоритму задачі формування та опис елементів матриці контролю комплексної системи захисту інформації (КСЗІ) інформаційних об’єктів комерційного банку В дипломному дослідженні матриця контролю стану побудови та експлуатації комплексної системи захисту інформації в комерційному банку представлена у вигляді ...
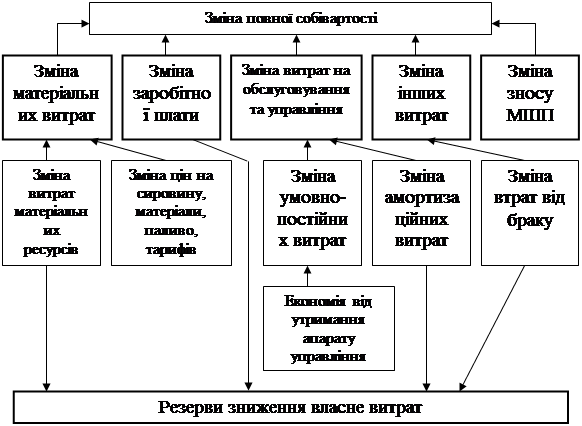
... і над плановим. Відомо, що собівартість є одним з головних джерел резервів підвищення ефективності роботи підприємства. Звідси сформуємо мету і задачі даної роботи. Метою даної роботи є підвищення ефективності роботи підприємства ВАТ «Дніпрополімермаш» шляхом управління собівартістю продукції. Відповідно, для досягнення поставленої мети необхідно вирішити наступні задачі: 1. Проаналізувати ...
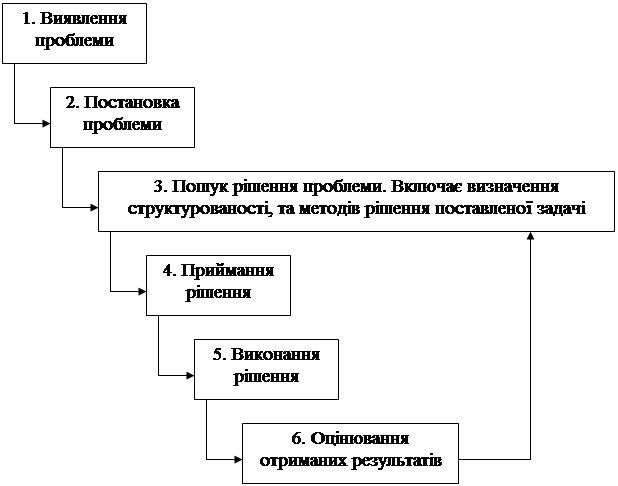
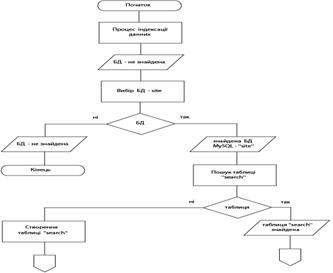
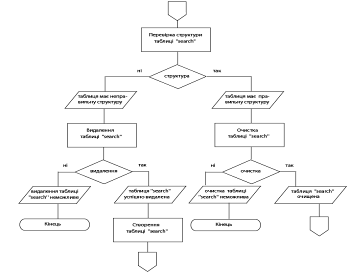
... в даній роботі, була опробована й досліджена в реальних умовах моєї професійної діяльності й показала свою працездатність і ефективність. 3. Розробка системи керування та актуалізації інформації web-сайту національного оператора Енергоринка 3.1 Вибір інструментарію для створення web-сайту та системи керування Перед тим, як безпосередньо перейти до створення Web-сайту Національного ...
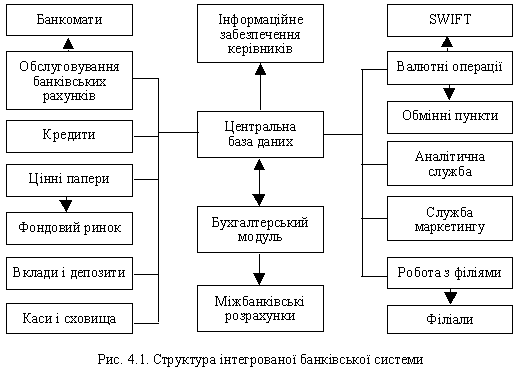
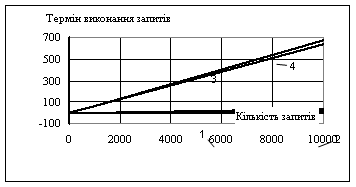
... маржі В такому випадку, макимізація прибутку відбувається за рахунок швидкого обороту коштів. Запропонований метод було прийнято як альтернативний метод визначення умов надання банківських послуг в Дніпропетровській філії АБ "Правексбанк", що дозволило збільшити фінансовий результат за перші 5 місяців 2008 року на 6 процентів. 4. АВТОМАТИЗОВАНА ІНФОРМАЦІЙНА СИСТЕМА Рис. 4.1 – Блок- ...

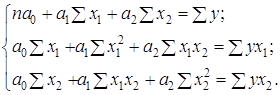
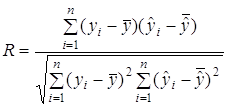

0 комментариев