Равномерное распределение
Условные законы распределения, условные числовые характеристики системы случайных величин, условие независимости случайных величин
Корреляция, свойство коэффициента корреляции. Линейная корреляция
Предельные теоремы теории вероятностей. Центральная предельная теорема Ляпунова
Основные категории статистики
Методы первичного анализа экспериментальных данных. Построение вариационных рядов и определение их основных характеристик
Размах вариации R = 210 – 150 = 60 шт
Сформулируйте определения полигона частот, гистограммы и кумуляты
При увеличении объёма выборки оценка должна сходиться по вероятности к истинному значению параметра. В этом случае оценку называют состоятельной
Статистики. Критерии. Критериальные случайные величины Пирсона, Стьюдента, Фишера-Снедекора
Навигация
Равномерное распределение
Основные понятия статистики
86945
знаков
23
таблицы
25
изображений
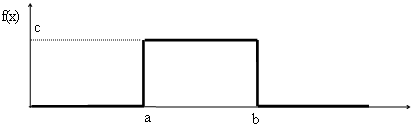
2.1 Равномерное распределение
х
Найдём константу с :
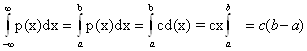
т.к.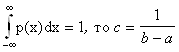 
.
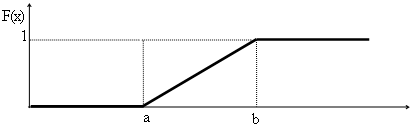
Функция распределения равномерного распределения:
Математическое ожидание: М(Х) =(а+в)/2, дисперсия D(X) = (b - a)2 /12
x
2.2 Показательный закон распределения
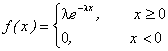
f(x)
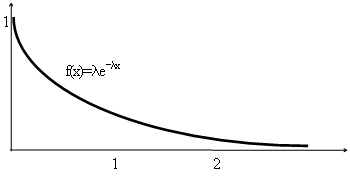
x
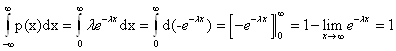
Функция распределения показательного распределения:
Математическое ожидание: М(Х) = 1/ λ, дисперсия D(X) =1/ λ2
2.3 Нормальное распределение – распределение Гаусса
Случайная величина имеет нормальное распределение (распределение Гаусса) и называется нормально распределенной, если ее плотность вероятности
По определению функция распределения:
Определение функция плотности распределения корректно, т.к. основное свойство распределения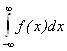 
= 1 выполнено, поскольку интеграл
| |
| |
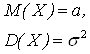
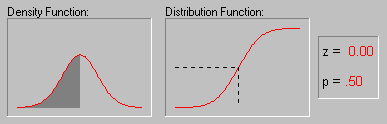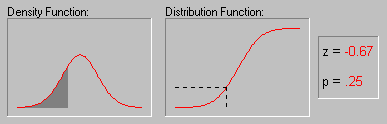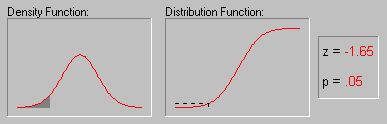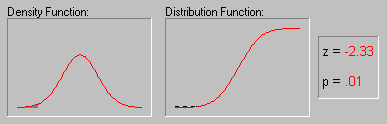
С нормальным распределением тесно связана функция Лапласа
Функцией Лапласа называется функция вида
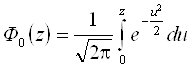
Функция Лапласа при z >0 определяет вероятность попадания стандартной нормальной случайной величины ( M(X) = 0, D(X) =1) в интервал (0, z)
Вероятность того, что значения нормальной случайной величины лежат в интервале (a, b) определяется следующим выражением:.
где 
3. Критериальные случайные величины. Распределение Стьюдента, Пирсона, Фишера - Снедекора
Случайные величины t – Стьюдента, χ2 – Пирсона, F – Фишера – Снедекора задаются табличным способом и используются в качестве критериальных в статистике
Контрольные вопросы
1.Дайте определение биномиальному распределению. Каковы его свойства и основные характеристики?
2. Дайте определение распределению Пуассона? Каковы его свойства и основные характеристики?
3. Какое распределение называется равномерным? Каковы его свойства и основные характеристики?
4. Какое распределение называется нормальным? Каковы его свойства и основные характеристики?
5. Напишите функцию распределения нормально распределенной случайной величины X, если M(Х) =3, D(X) =σ2= 16.
6. Задана случайная величина X, распределенная нормально с параметрами
M(Х) = 0 и σ = 2.
Найдите вероятность того, что эта случайная величина принимает значение
а) из отрезка [-1,2]; б) меньшее -1; в) большее 2; г) отличное от своего среднего значения по абсолютной величине не больше, чем на 1.
7. Задана дискретная случайная величина Z – индикатор испытаний: Z =1, если в соответствующем испытании событие А появилось и Z = 0 в противоположном случае. Закон распределения имеет вид:
| Z | 0 | 1 |
| P | q | p |
Найти математическое ожидание и дисперсию Z.
8. Дискретная пуассоновская случайная величина X p имеет распределение:
Вычислите математическое ожидание и дисперсию дискретной пуассоновской случайной величины
9. Задана равномерно распределённая на отрезке [a;b] непрерывная случайная величина Х:
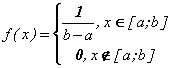
Вычислите математическое ожидание и дисперсию случайной величины Х.
10. Задана непрерывная случайная величина Y, имеющая показательное распределение:
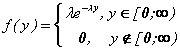
Вычислите математическое ожидание и дисперсию случайной величины Y.
11. Задана непрерывная случайная величина X, имеющая нормальное распределение:
Вычислите математическое ожидание и дисперсию случайной величины X.
Тема 1.5. Системы случайных величин
1. Закон распределения, функция распределения системы случайных величин, их свойства.
2. Условные законы распределения, условные числовые характеристики системы случайных величин, условие независимости случайных величин.
3. Функцией регрессии. Линейная регрессия.
4. Корреляция, свойство коэффициента корреляции. Линейная корреляция
1. Закон распределения, функция распределения системы случайных величин, их свойства
Рассмотренные выше случайные величины были одномерными, т.е. определялись одним числом, однако, существуют также случайные величины, которые определяются двумя, тремя и т.д. числами. Такие случайные величины называются двумерными, трехмерными и т.д.
В зависимости от типа, входящих в систему случайных величин, системы могут быть дискретными, непрерывными или смешанными, если в систему входят различные типы случайных величин.
Более подробно рассмотрим системы двух случайных величин.
Определение. Законом распределения системы случайных величин называется соотношение, устанавливающее связь между областями возможных значений системы случайных величин и вероятностями появления системы в этих областях.
Определение. Функцией распределения системы двух случайных величин называется функция двух аргументов F(x, y), равная вероятности совместного выполнения двух неравенств X<x, Y<y.
Отметим следующие свойства функции распределения системы двух случайных величин:
1) Если один из аргументов стремится к плюс бесконечности, то функция распределения системы стремится к функции распределения одной случайной величины, соответствующей другому аргументу.
2) Если оба аргумента стремятся к бесконечности, то функция распределения системы стремится к единице.
3) При стремлении одного или обоих аргументов к минус бесконечности функция распределения стремится к нулю.
4) Функция распределения является неубывающей функцией по каждому аргументу.
5) Вероятность попадания случайной точки (X, Y) в произвольный прямоугольник со сторонами, параллельными координатным осям, вычисляется по формуле:
Плотность распределения системы двух случайных величин.
Определение. Плотностью совместного распределения вероятностей двумерной случайной величины (X, Y) называется вторая смешанная частная производная от функции распределения.
Если известна плотность распределения, то функция распределения может быть легко найдена по формуле:
Двумерная плотность распределения неотрицательна и двойной интеграл с бесконечными пределами от двумерной плотности равен единице.
По известной плотности совместного распределения можно найти плотности распределения каждой из составляющих двумерной случайной величины.
; 
;
Похожие работы
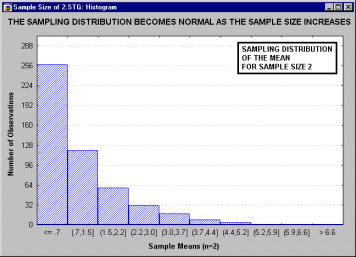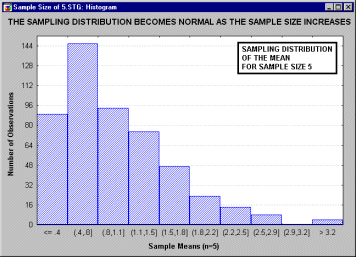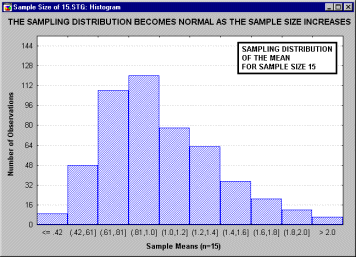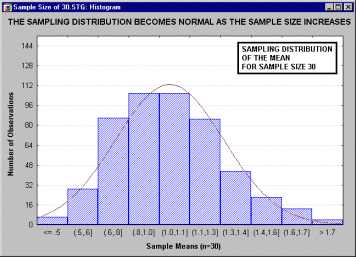
... , что все это рассуждение основано на предположении о нормальности распределения этих повторных выборок (т.е. нормальности выборочного распределения). Это предположение обсуждается в следующем разделе. Все ли статистики критериев нормально распределены? Не все, но большинство из них либо имеют нормальное распределение, либо имеют распределение, связанное с нормальным и вычисляемое на основе ...
... признак. Классификация. Для изучения общей теории статистики необходимо рассмотреть основные понятия на которых будет основываться все дальнейшее изложение материала. Т.к. статистика имеет дело с массовыми явлениями, то основным понятием является статистическая совокупность. Статистическая совокупность – это множество объектов или явлений изучаемых статистикой, которые имеют один или несколько ...
... пер- вичных статистических материалов, и вторичные, характеризуемые в процессе обработки и анализа данных. ПОКАЗАТЕЛЬ - одно из основных понятий статистики, под которым имеется в виду обобщенная колличественная характеристика социально-экономических явлений и процессов в их качественной определенности в условиях конкрет- ного места и времени. Примерами конкретных социально-экономических показате ...
... . Совокупность заведений, занимающихся однородным видом деятельности, представляет собой отрасль. Для количественного описания состояния и функционирования экономики в системе национальных счетов используются понятия запасов и потоков. Запасы отражают все виды активов и пассивов в экономике и отражаются в учете на определенную дату. Потоки отражают любые действия по созданию, преобразованию, ...
0 комментариев