Навигация
Статистики. Критерии. Критериальные случайные величины Пирсона, Стьюдента, Фишера-Снедекора
3. Статистики. Критерии. Критериальные случайные величины Пирсона, Стьюдента, Фишера-Снедекора
Напомним, что любую функцию j = j (х1, ….хn), зависящую от выборочных переменных и поэтому являющуюся случайной величиной, принято называть статистикой. Таким образом, все оценки являются статистиками, случайными величинами. В связи с таким свойствами оценок, они должны быть проверены на значимость. Для этого используются критериальные случайные величины Пирсона, Стьюдента, Фишера-Снедекора.
4. Проверка статистических гипотезСтандартными задачами математической статистики являются задачи определения класса (вида) распределения генеральной совокупности и определение её основных числовых характеристик. Эти задачи математическая статистика решает в виде выдвижения гипотез, а не прямым расчетом. Это связано с тем, исходные данные для статистических расчетов являются случайными величинами и полученные результаты расчета тоже есть случайные величины. Поэтому каждый расчетный результат должен быть дополнен вероятностью его правильности (или ошибки), следовательно, он является гипотетическим.
Определение 1. Статистической гипотезой называют гипотезу о виде неизвестного распределения или о параметрах известного распределения.
Наряду с данной гипотезой рассматривают и противоречащую ей гипотезу. В случае, когда выдвинутая гипотеза отвергается, обычно принимается противоречащая ей гипотеза.
Определение 2. Нулевой (основной) называют выдвинутую гипотезу H0. Конкурирующей (альтернативной) называют гипотезу H1, которая противоречит основной.
Пример. Нулевая гипотеза H0 : генеральная совокупность распределена по нормальному закону, тогда гипотеза H1 : генеральная совокупность не распределена по нормальному закону.
Пример. Нулевая гипотеза H0 : Мх = 20 ( т.е. математическое ожидание нормально распределённой величины равно 20), тогда гипотеза H1 может иметь вид H1: Мх ![]() 20.
20.
Проверку правильности или неправильности выдвинутой гипотезы проводят статистическими методами. В результате такой проверки может быть принято правильное или неправильное решение. Поэтому различают ошибки двух родов. Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза. Ошибка второго рода состоит в том, что будет принята неправильная гипотеза.
Идея, которая используется при проверке статистических гипотез, заключается в следующем.
Вводится некоторая вычисляемая случайная величина, называемая критерием, распределение которой заранее известно и которая характеризует отклонение выборочных характеристик от их гипотетических значений. В предположении о справедливости гипотезы H0 фиксируем заранее некоторый уровень значимости α (допустимую вероятность ошибки того, что принимается гипотеза H0, а на самом деле верна гипотеза H1) считая , что в одиночном эксперименте событие с вероятностью, меньшей α, практически не происходят. По α находим такое число![]() , что бы выполнялось соотношение:
, что бы выполнялось соотношение:
![]()
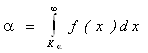
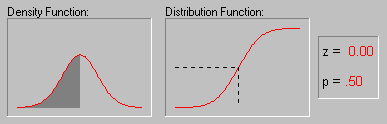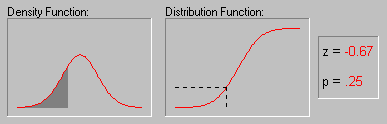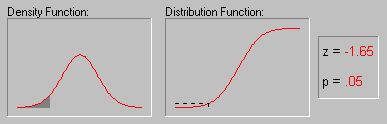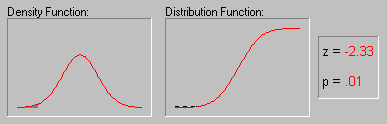
Пусть теперь КВ – вычисленное по выборке значение критерия. Если окажется ![]() , то в предположении о справедливости гипотезы H0 произошло «практически» невозможное событие и поэтому выдвинутую гипотезу H0 следует отвергнуть и принять гипотезу H1. В противном случае, можно считать, что наблюдения не противоречат гипотезе H0. На приведенных рисунках показано функция плотности распределения случайной величины – критерия χ2 (Рис. 1 ) и кривая уровню значимости для распределения χ2 ( Рис.2.). Уровень значимости равен интегралу от функции плотности распределения в пределах от
, то в предположении о справедливости гипотезы H0 произошло «практически» невозможное событие и поэтому выдвинутую гипотезу H0 следует отвергнуть и принять гипотезу H1. В противном случае, можно считать, что наблюдения не противоречат гипотезе H0. На приведенных рисунках показано функция плотности распределения случайной величины – критерия χ2 (Рис. 1 ) и кривая уровню значимости для распределения χ2 ( Рис.2.). Уровень значимости равен интегралу от функции плотности распределения в пределах от ![]() до ∞, т.е.:
до ∞, т.е.:
По заданному уровню значимости α находят значение нижнего предела ![]() =
= ![]()
Так, например, при α = 0.05 из графика (Рис. 1.) определяем ![]() = 7.814
= 7.814
Рис. 1.
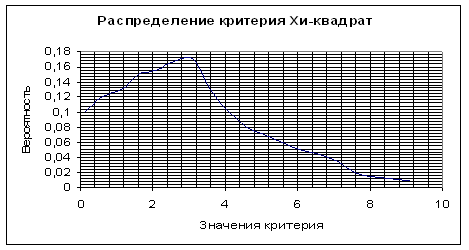
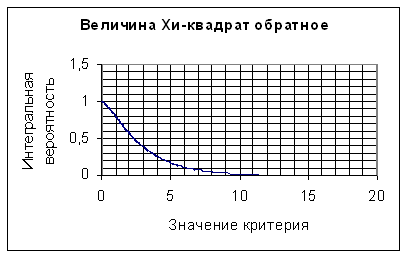
Рис. 2.
Критерий Фишера. Проверка гипотезы о равенстве дисперсий.
Задача проверки «статистического» равенства дисперсий в двух выборках играет в математической статистике большую роль, т.к. именно дисперсия определяет такие исключительные важные конструктивные и технологические и экономические показатели, как точность машин и приборов, погрешность измерительных методик, точность технологических процессов, состояние экономической конъюнктуры. и т.д.
В качестве критерия F (критерий Фишера) для проверки гипотезы о равенстве дисперсий в двух генеральных совокупностях по независимым выборкам из них строится случайная величина, равная отношению двух «исправленных» дисперсий , предполагая, что генеральная совокупность распределена нормально.
![]()
Доказано, что эта случайная величина имеет распределение Фишера с к1 = n1 – 1 и k2 = n2 – 1 степенями свободы, где n1 и n2 – объёмы первой и второй выборок. Обычно в качестве числителя берут большую из «исправленных» дисперсий ![]() .
.
Чтобы проверить гипотезу о равенстве дисперсий, надо построить критическую область для критерия F. В качестве критической области принимаются два интервала: интервал больших значений критерия, удовлетворяющий неравенству F >F2 и интервал малых значений 0 < F < F1, причём критические точки занимают такое положение на оси критерия, чтобы удовлетворять следующим равенствам:
![]()
![]()
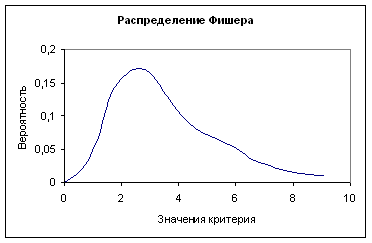
где ![]() – площади под кривой распределения (см. Рис.3).
– площади под кривой распределения (см. Рис.3).
Такой выбор критической области обеспечивает большую чувствительность критерия. Оказывается, что достаточно определить правую критическую точку F2; последнее объясняется тем, что если величина
![]()
имеет распределение Фишера ( с k1 и k2 степенями свободы), то и
![]()
также имеет распределение Фишера (с k1 и k2 степенями свободы). Поэтому в таблицах табулируются только правые точки этого распределения.
Если полученное по выборке значение критерия выходит за правую критическую точку F2, гипотезу о равенстве дисперсий следует отбросить, в противном случае гипотеза о равенстве дисперсий не противоречит наблюдениям.
![]()
|
|
Пример. При проведении тестирования на профессиональную пригодность были подвергнуты испытанию две группы: в первой группе – 10 человек, во второй группе – 15 человек. По данным этих тестов были посчитаны «исправленные» эмпирические дисперсии, оказавшиеся равными для первой группы ![]() и для второго
и для второго ![]() . Требуются проверить с уровнем значимости α=0,1 гипотезу о равенстве дисперсий – уровнем подготовленности.
. Требуются проверить с уровнем значимости α=0,1 гипотезу о равенстве дисперсий – уровнем подготовленности.
Р е ш е н и е.
Вычислим выборочное значение критерия
F = ![]()
![]()
По таблицам распределения Фишера и при α = 0,05 и степенях свободы k1 = n1 –1 = 9 и k2 = n2 –1 = 14 находим критическую точку F2 = 2,65. Выборочное значение критерия оказалось меньше критического, и, следовательно, предположение о равенстве дисперсий не противоречит наблюдениям. Иными словами, нет оснований считать, что две группы ![]() обладают разным уровнем подготовленности.
обладают разным уровнем подготовленности.
Пример. Оценивается валидность двух различных однотипных тестов. Подвергаются испытанию одна и та же группа с составе 20 человек. По данным тестирования были вычислены исправленные дисперсии, они оказались равными:
![]() ,
, ![]() .
.
Определить валидность однотипных тестов.
Р е ш е н и е.
Вычисляем выборочное значение критерия
![]()
По таблицам распределения Фишера и при α = 0,05 и степенях свободы k1 = n1 –1 = 19 и k2 = n2 –1 = 19 находим критическую точку F2 = 2,16. Таким образом, выборочное значение критерия попадает в критическую область и гипотезу о равенстве дисперсий следует отбросить, т.е. по данным двух выборок испытуемых валидность тестов существенно отличается друг от друга.
Критерий Пирсона χ2. Проверка гипотез о законе распределений .
В предыдущем параграфе были рассмотрены некоторые способы оценки параметров заранее известного закона распределения. Однако в ряде случае сам вид закона распределения является гипотетическим и нуждается в статистической проверке. Гипотезы о виде закона распределения выдвигаются на основе результатов построения эмпирических функций распределения или гистограмм.
Рассмотрим вопрос о критерии проверки по данным выборки гипотезы о том, что данная случайная величина Х имеет функцию распределения F(х). Необходимо ввести некоторую случайную величину- критерий К, основанный на выборе определённой меры расхождения эмпирического и теоретического распределений. Наиболее распространённым является критерий Пирсона χ2 (хи-квадрат). Суть критерия Пирсона состоит в следующем.. Область изменения случайной величины разбивается на конечное число интервалов: ![]()
Δх1, Δx2, …. Δxl (если это вся числовая ось, то первый и последний l-ый интервал будут бесконечными). Пусть mi – число значений выборки n, попавших в интервал Δхi , а pi – вероятность того, что случайная величина Х примет значения, принадлежащие Δхi при данном распределении F(x). Эта вероятность pi вычисляется по известным соотношениям:
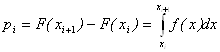
где xi и xi+1 – начальная и конечная точка интервала Δхi. Очевидно, выполняются условия
![]()
По найденным pi находим математические ожидания попаданий случайной величины Х в интервал Δхi. при n испытаниях, которые равны npi. В качестве меры расхождения выборочных m1, m2, ….ml и теоретических np1,np2,….npl характеристик вводится следующая величина:
![]()
Доказано, что введенная таким образом случайная величина при неограниченном увеличении n распределена по закону ![]() с r степенями свободы, где r = l – 1 – k, а k равно числу параметров, оцениваемых по данным выборке. Если все параметры закона распределения известны заранее (не на основе выборки!, например, при равномерном распределении), то к = 0. Остаётся , задавшись определённым уровнем значимости α , указать критическую область критерия. Обозначим
с r степенями свободы, где r = l – 1 – k, а k равно числу параметров, оцениваемых по данным выборке. Если все параметры закона распределения известны заранее (не на основе выборки!, например, при равномерном распределении), то к = 0. Остаётся , задавшись определённым уровнем значимости α , указать критическую область критерия. Обозначим ![]() число, найденное из условия
число, найденное из условия
![]()
В качестве критической области примем интервал ![]() .Определив
.Определив ![]() по данным выборки, мы получим одно из двух: или
по данным выборки, мы получим одно из двух: или ![]() (т.е. выборочное значение критерия попадает в критическую область и тогда расхождение выборочных данных с гипотетическим законом распределения существенно, а поэтому гипотеза H0 отвергается и принимается гипотеза H1. Если
(т.е. выборочное значение критерия попадает в критическую область и тогда расхождение выборочных данных с гипотетическим законом распределения существенно, а поэтому гипотеза H0 отвергается и принимается гипотеза H1. Если ![]() , то отличие эмпирического закона от теоретического считается несущественным и принимается гипотеза H0 о статистическом равенстве эмпирического и теоретического законов распределения.
, то отличие эмпирического закона от теоретического считается несущественным и принимается гипотеза H0 о статистическом равенстве эмпирического и теоретического законов распределения.
Замечание. Случайная величина – критерий ![]() , вычисленная по выборочным данным, только при n →∞ распределена по закону
, вычисленная по выборочным данным, только при n →∞ распределена по закону ![]() . Возникает естественный вопрос о правомерности использования этого распределения при конечном n. Принято считать это приближение достаточным для практических расчетов, если для всех интервалов npi
. Возникает естественный вопрос о правомерности использования этого распределения при конечном n. Принято считать это приближение достаточным для практических расчетов, если для всех интервалов npi ![]() 10.Если же имеются интервалы, для которых npi <10, то рекомендуется их объединять с соседними так, чтобы новые интервалы уже удовлетворяли указанному условию.
10.Если же имеются интервалы, для которых npi <10, то рекомендуется их объединять с соседними так, чтобы новые интервалы уже удовлетворяли указанному условию.
Пример. Имеются опытные данные о числе звонков в службу аварийного помощи в течение рабочего дня – таблица 1.
| Интервалы (часы смены) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Число звонков | 16 | 27 | 17 | 15 | 24 | 19 | 11 | 15 |
Проверить с помощью критерия Пирсона и при уровне значимости α = 0,05 гипотезу о равномерном распределении числа звонков в психологическую службу в течение дня.
Решение. Постоим эмпирическую функцию плотности распределения вызовов. Рис.4.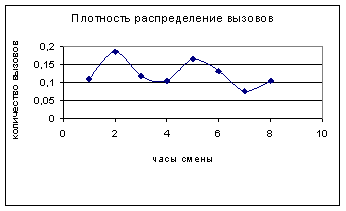
Приведённый рисунок позволяет выдвинуть гипотезу о равномерном распределении звонков в службу психологической помощи, т.к. плотность звонков колеблется около некоторого среднего значения. В качестве интервалов Δхi берём соответствующие часы смены. Так как предполагается оценивать равномерное распределение, то все pi =
Таблица 2.
| Интервалы (часы смены) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Число звонков mi | 16 | 27 | 17 | 15 | 24 | 19 | 11 | 15 |
| Математические ожидания npi | 18 | 18 | 18 | 18 | 18 | 18 | 18 | 18 |
| mi - npi | -2 | 9 | -1 | -3 | 6 | 1 | -7 | -3 |
|
| 0.22 | 4.5 | 0.06 | 0.5 | 2.00 | 0.06 | 2.72 | 0.5 |
Σ =10.56
Число степеней свободы равно r = l – 1 – k = 7 ( k = 0, т.к. единственный параметр распределения – рабочее время смены , т.е. длина отрезка b-a – заранее известно). При данном уровне значимости α = 0,05 по таблице находим соответствующее значение ![]() =14,07. Вычисленное значение
=14,07. Вычисленное значение ![]() = 10,56 лежит левее критического значения, т.е. в области допустимых значений, и поэтому нет оснований считать гипотезу H0 о равномерном распределении противоречащей наблюдениям.
= 10,56 лежит левее критического значения, т.е. в области допустимых значений, и поэтому нет оснований считать гипотезу H0 о равномерном распределении противоречащей наблюдениям.
Пример. Имеются результаты опроса группы молодёжи, состоящей из 200 человек, о возрасте первого употреблении наркотиков. Результаты представлены в виде интервального вариационного ряда (Таблица 1.):
Таблица 1.
| Интервал возрастов | 11-12 | 12-13 | 13-14 | 14-15 | 15-16 | 16-17 | 17-18 | 18-19 | 19-20 | 20-21 |
| Количество человек в группе | 7 | 12 | 14 | 25 | 48 | 42 | 24 | 13 | 10 | 5 |
Требуется с помощью критерия Пирсона и при уровне значимости α = 0,05 оценить гипотезу о нормальном распределении возрастов начала употребления наркотиков, тем самым подтвердив гипотезу, что явление наркомании порождено множеством различных причин.
Решение. Построим экспериментальную функцию плотности распределения распределение. Поскольку вариационный ряд интервальный следует перейти к серединам интервалов и заменить абсолютные частоты – частотами относительными. В результате получим (Таблица 2; Рис 2):
Таблица 2.
| Середины интервалов | 11,5 | 12,5 | 13,5 | 14,5 | 15,5 | 16,5 | 17,5 | 18,5 | 19,5 | 20,5 |
| Относительные частоты | 0,035 | 0,06 | 0,07 | 0,125 | 0,24 | 0,21 | 0,12 | 0,065 | 0,05 | 0,025 |
|
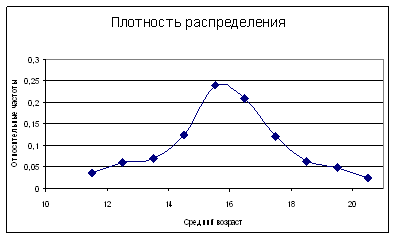 Рис.5
Рис.5 Полученная кривая имеет колоколообразную форму, поэтому есть основания к выдвижению гипотезы о нормальном распределении возрастов начала употребления наркотиков.
Результаты вычислений сведем в таблицу 3.
Таблица 3.
| № интервала | Границы интервала | x*i | mi | νi | pi | npi |
|
| 1 | 11,12 | 11,5 | 7 | 0.035 | 0,0187 | 3,7383 | 2,8458 |
| 2 | 12,13 | 12,5 | 12 | 0.06 | 0,0485 | 9,6940 | 0,5486 |
| 3 | 13,14 | 13,5 | 14 | 0.07 | 0,0984 | 19,6702 | 1,6345 |
| 4 | 14,15 | 14,5 | 25 | 0.125 | 0,1562 | 31,2318 | 1,2435 |
| 5 | 15,16 | 15,5 | 48 | 0.24 | 0,1940 | 38,8031 | 2,1798 |
| 6 | 16,17 | 16,5 | 42 | 0.21 | 0,1886 | 37,7239 | 0,4847 |
| 7 | 17,18 | 17,5 | 24 | 0.12 | 0,1435 | 28,6978 | 0,7690 |
| 8 | 18,19 | 18,5 | 13 | 0.065 | 0,0854 | 17,0829 | 0,9758 |
| 9 | 19,20 | 19,5 | 10 | 0.05 | 0,0398 | 7,9571 | 0,5245 |
| 10 | 20,21 | 20,5 | 5 | 0.025 | 0,0145 | 2,9002 | 1,5203 |
Сумма: 12,72645
Среднее значение возраста, впервые употребляющие наркотики, равно 15,885
Подправленная дисперсия возрастов, впервые употребляющих наркотики, равна 4,077. Стандартное отклонение возрастов, впервые употребляющих наркотики, равно 2,019
Полученные характеристики позволяют с помощью таблиц гауссовой кривой вычислить вероятности средних возрастов, впервые употребляющих наркотики. Результаты вычислений представлены на рисунке 6. Графики экспериментальных относительных частот и теоретических вероятностей практически совпали друг с другом из-за масштабирования. Чтобы показать существующее расхождение между теоретическим и экспериментальным распределением построим графики абсолютных частот средних значений возрастов – рисунок 7.
|

Рис.6
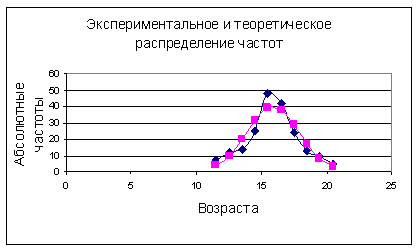
Рис.7.
Вычислим значение критерия – случайной величины χ2. Оно равно сумме значений последнего столбца таблицы - 12,726. Критическое значение χ2 при уровне значимости 0,05 и степенях свободы, равных r = 10 – 1 – k = 10 – 1 – 2 = 7 , определяется значением 14,067. Таким образом, нет оснований отвергать гипотезу H0 о нормальном законе распределения возрастов лиц, впервые употребляющих наркотические вещества, тем самым мы подтверждаем экспериментально мнение специалистов, что проблема наркомании имеет комплексный характер.
Контрольные вопросы:
1 Дайте определение точечной и интервальной оценке.
Сформулируйте основные требования к точечным оценкам и раскройте их смысл
Дайте определения уровню значимости, ошибки первого и второго рода.
4. Для вариационного ряда Темы 2.1. найти точечные оценки параметров нормального закона распределения, записать соответствующую формулу для плотности вероятностей f(x) и рассчитать теоретические относительные частоты. Построить график плотности распределения на гистограмме относительных частот, а теоретические относительные частоты показать на полигоне относительных частот.
5. Найти интервальные оценки параметров нормального закона распределения, приняв доверительную вероятность = 0,95 и 0,99.
6. Проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности с эмпирическим распределением выборки, используя критерий Пирсона при уровнях значимости 0,01; 0,05.
Тема 2.3. Статистические методы обработки экспериментальных данных
1. Метод наименьших квадратов (МНК).
2. Регрессионный анализ
3. Корреляционный анализ
Конспект лекции
Уравнение парной линейной корреляционной связи называется уравнением парной регрессии и имеет вид:
у = а + bх, (1)
где у - среднее значение результативного признака при определенном значении факторного признака х;
а - свободный член уравнения;
b - коэффициент регрессии, измеряющий среднее отношение отклонения результативного признака от его средней величины к отклонению факторного признака от его средней величины на одну единицу его измерения - вариация у, приходящаяся на единицу вариации х.
Уравнение (1) определяется по данным о значениях признаков х и у в изучаемой совокупности, состоящей из п единиц. Параметры уравнения а и b находятся методом наименьших квадратов (МНК).
Исходное условие МНК для линейной связи имеет вид:
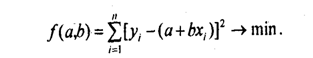
Для отыскания значений параметров а и b, при которых f(a,b) принимает минимальное значение, частные производные функции приравниваем нулю и преобразуем получаемые уравнения, которые называются нормальными уравнениями МНК для линейной формы уравнения регрессии:
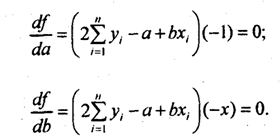
Отсюда система нормальных уравнений имеет вид:
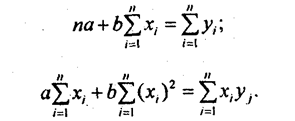
Нормальные уравнения МНК для прямой линии регрессии являются системой двух уравнений с двумя неизвестными а и b. Все остальные величины, входящие в систему, определяются по исходной информации. Таким образом, однозначно вычисляются при решении этой системы уравнений оба параметра уравнения линейной регрессии.
Если первое нормальное уравнение разделить на п, получим:
![]() (2)
(2)
По уравнению (2) обычно на практике вычисляется свободный член уравнения регрессии а. Параметр b вычисляется по преобразованной формуле, которую можно вывести, решая систему нормальных уравнений относительно b:
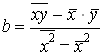 . (3)
. (3)
Так как знаменатель этого выражения есть не что иное, как дисперсия признака х, т. е. σ2, то можно записать формулу коэффициента регрессии в виде:
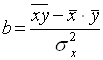 (4)
(4)
Подставив в (3) выражение для s2x, получим:
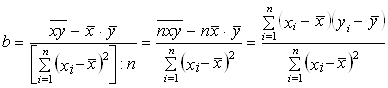 . (5)
. (5)
Параметры уравнения регрессии можно вычислить через определители:
![]() (6)
(6)
где D - определитель системы;
Da - частный определитель, получаемый в результате замены коэффициентов при а свободными членами из правой части системы уравнений;
Db - частный определитель, получаемый в результате замены коэффициентов при b свободными членами из правой части системы уравнений.
Коэффициент парной линейной регрессии, обозначенный ![]() , имеет смысл показателя силы связи между вариацией факторного признака х и вариацией результативного признака у. Он измеряет среднее по совокупности отклонение у от его средней величины при отклонении признака х от своей средней величины на принятую единицу измерения.
, имеет смысл показателя силы связи между вариацией факторного признака х и вариацией результативного признака у. Он измеряет среднее по совокупности отклонение у от его средней величины при отклонении признака х от своей средней величины на принятую единицу измерения.
Теснота парной линейной корреляционной связи, как и любой другой показатель, может быть измерена корреляционным отношением h. Кроме того, при линейной форме уравнения применяется другой показатель тесноты связи - коэффициент корреляции rxy. Этот показатель представляет собой стандартизованный коэффициент регрессии, т. е. коэффициент, выраженный не в абсолютных единицах измерения признаков, а в долях среднего квадратического отклонения результативного признака:
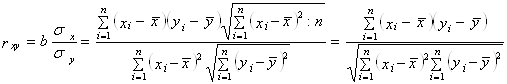 . (7)
. (7)
Коэффициент корреляции был предложен английским статистиком и философом Карлом Пирсоном (1857 - 1936). Его интерпретация такова: отклонение признака-фактора от его среднего значения на величину своего среднего квадратического отклонения в среднем по совокупности приводит к отклонению признака-результата от своего среднего значения на rxy его среднего квадратического отклонения.
В отличие от коэффициента регрессии b коэффициент корреляции не зависит от принятых единиц измерения признаков, а стало быть, он сравним для любых признаков.
Обычно считают связь сильной, если r ³. 0,7; средней тесноты, при 0,5 £ r £ 0,7; слабой при r < 0,5. Квадрат коэффициента корреляции называется коэффициентом детерминации:
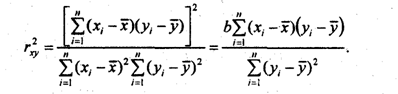
Эта формула используется при. анализе множественной корреляции. Умножив числитель и знаменатель последнего выражения на ![]() получим:
получим:
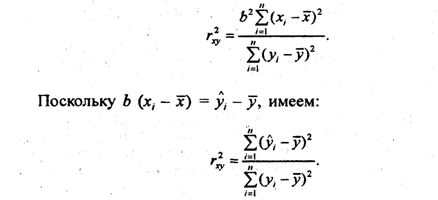
и окончательно, коэффициент корреляции принимает вид:
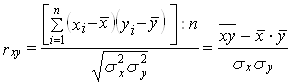 . (8)
. (8)
Эта формула соответствует формуле (7) для коэффициента регрессии.
Средние квадратическое отклонение можно выразить через средние величины признака:
![]() .
.
Подставив эти выражения в (8), получим:
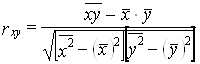 . (9)
. (9)
Эта формула (9) удобнее для расчетов, если средние величины признаков и средние квадраты индивидуальных величин вычислены ранее.
Рассмотрим фактический пример анализа корреляционной парной линии связи по данным 16 сельхозпредприятий о затратах на 10 гектар пашни и о урожайности с 1 гектара. (табл.1).
Средние значения признаков: x̅ = 1605 руб.; у̅ = 35,2 ц/голов.
Сопоставляя знаки отклонений признаков x и у от средних величин, видим явное преобладание совпадающих по знакам пар отклонений: их 14 и только 2 пары несовпадающих знаков.
Таблица 1.
Корреляция между затратами и урожайностью
| Номера единиц сово-куп-ности | Затраты на 10 гектар руб хi | Урожайность с гектара, ц, yi | xi - x̅ | yi - y̅ | (xi - x̅) ´ ´ (yi - y̅) | (xi - x̅)2 | (yi - y̅)2 | Расчетные значения урожайности , ц |
| 1 | 1602 | 34,2 | -3 | -1,0 | +3,0 | 9 | 1,00 | 35,1 |
| 2 | 1199 | 19,6 | -406 | -15,6 | +6333,6 | 164836 | 243,36 | 21,1 |
| 3 | 1321 | 27,3 | -283 | -7,9 | +2235,7 | 80089 | 62,41 | 25,3 |
| 4 | 1678 | 32,5 | +73 | -2,7 | -197,1 | 5329 | 7,29 | 37,7 |
| 5 | 1600 | 33,2 | -5 | -2,0 | +10,0 | 25 | 4,00 | 35,0 |
| 6 | 1355 | 31,8 | -250 | -3,4 | +850,0 | 62500 | 11,56 | 26,5 |
| 7 | 1413 | 30,7 | -192 | ^,5 | +864,0 | 36864 | 20,25 | 28,5 |
| 8 | 1490 | 32,6 | -115 | -2,6 | +299,0 | 13225 | 6,76 | 31,2 |
| 9 | 1616 | 26,7 | +11 | -8,5 | -93,5 | 121 | 72,25 | 35,6 |
| 10 | 1693 | 42,4 | +88 | +7,2 | +633,6 | 7744 | 51,84 | 38,2 |
| 11 | 1665 | 37,9 | +60 | +2,7 | +162,0 | 3600 | 7,29 | 37,3 |
| 12 | 1666 | 36,6 | +61 | +1,4 | +85,4 | 3721 | 1,96 | 37,3 |
| 13 | 1628 | 38,0 | +23 | +2,8 | +64,4 | 529 | 7,84 | 36,0 |
| 14 | 1604 | 32,7 | -1 | -2,5 | +2,5 | 1 | 6,25 | 35,2 |
| 15 | 2077 | 51,7 | +472 | +16,5 | +7788 | 222784 | 272,25 | 51,6 |
| 16 | 2071 | 55,3 | +466 | +20,1 | +9366,6 | 217156 | 404,01 | 51,4 |
| S 25678 | 563,2 | - | - | +28473,7 | 818533 | 1180,32 | 563,0 | |
Вычислим на основе итоговой строки табл1. параметр парной линейной корреляции:
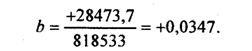
Он означает, что в среднем по изучаемой совокупности отклонение затрат от средней величины на 1 руб. приводило к отклонению с тем же знаком средней урожайности на 0,0347 ц, т. е. на 3,47 кг на 1га. При нестрогой интерпретации говорят: «С увеличением затрат на 1 руб. в среднем урожайность возрасла на 3,47 кг». Свободный член уравнения регрессии : а = 35,2 - 0,0347 • 1605 = - 20,49.
Уравнение регрессии в целом имеет вид:
![]()
Отрицательная величина свободного члена уравнения означает, что область существования признака у не включает нулевого значения признакам и близких значений. Если же область существования результативного признака ![]() включает нулевое значение признака-фактора, то свободный член является положительным и означает среднее значение результативного признака при отсутствии данного фактора, например среднюю урожайность картофеля при отсутствии органических удобрений.
включает нулевое значение признака-фактора, то свободный член является положительным и означает среднее значение результативного признака при отсутствии данного фактора, например среднюю урожайность картофеля при отсутствии органических удобрений.
Графическое изображение корреляционной связи по данным табл.1. приведено на рис. 1.
Коэффициент корреляции, рассчитанный на основе табл. 8.1,
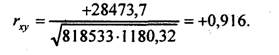
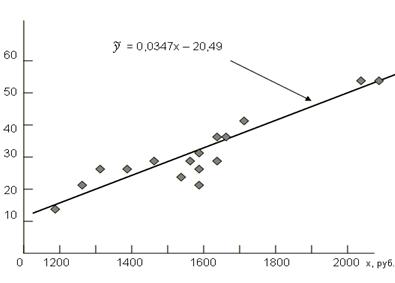
Рис. 1. Корреляция затрат с урожайностью
Контрольные вопросы:
1. Сформулируйте суть метода наименьших квадратов и условия его применимости.
2. Что означает несмещенность, состоятельность и эффективность оценок МНК?
3. Дайте определение регрессионной форме связи.
4. Что такое теснота корреляционной зависимости?
5. Найти выборочное уравнение линейной регрессии признака Y на признаке X и коэффициент их корреляции по экспериментальным данным из таблицы
| nij | X | ||||||
| 10 | 15 | 20 | 25 | 30 | 35 | ||
| Y | 30 | 2 | 6 | ||||
| 40 | 4 | 4 | |||||
| 50 | 7 | 35 | 8 | ||||
| 60 | 2 | 10 | 8 | ||||
| 70 | 5 | 6 | 3 | ||||
Похожие работы
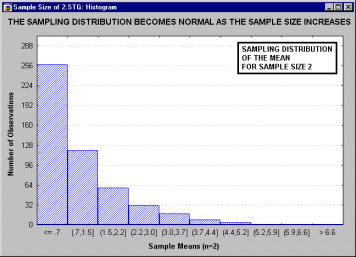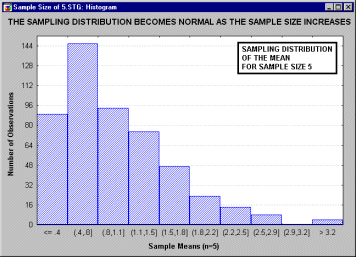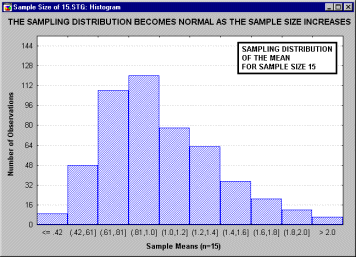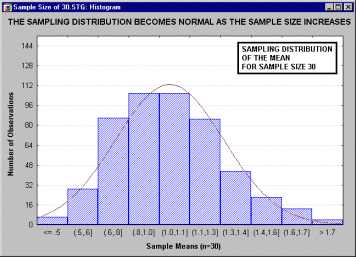
... , что все это рассуждение основано на предположении о нормальности распределения этих повторных выборок (т.е. нормальности выборочного распределения). Это предположение обсуждается в следующем разделе. Все ли статистики критериев нормально распределены? Не все, но большинство из них либо имеют нормальное распределение, либо имеют распределение, связанное с нормальным и вычисляемое на основе ...
... признак. Классификация. Для изучения общей теории статистики необходимо рассмотреть основные понятия на которых будет основываться все дальнейшее изложение материала. Т.к. статистика имеет дело с массовыми явлениями, то основным понятием является статистическая совокупность. Статистическая совокупность – это множество объектов или явлений изучаемых статистикой, которые имеют один или несколько ...
... пер- вичных статистических материалов, и вторичные, характеризуемые в процессе обработки и анализа данных. ПОКАЗАТЕЛЬ - одно из основных понятий статистики, под которым имеется в виду обобщенная колличественная характеристика социально-экономических явлений и процессов в их качественной определенности в условиях конкрет- ного места и времени. Примерами конкретных социально-экономических показате ...
... . Совокупность заведений, занимающихся однородным видом деятельности, представляет собой отрасль. Для количественного описания состояния и функционирования экономики в системе национальных счетов используются понятия запасов и потоков. Запасы отражают все виды активов и пассивов в экономике и отражаются в учете на определенную дату. Потоки отражают любые действия по созданию, преобразованию, ...
0 комментариев